CF1876C - Autosynthesis

原题链接 参考文章

其实不是我这个水平能做出的题……但是更主要是学基环树。

首先是用i连边指向a[i]，一个点有一个出边，就是基环树森林。然后观察图的性质，发现：

没被圈的点总是指向被圈了的点，而被圈了的点指向哪种点都行（也可以认为是出边没了），就变成了染色的问题。

参考文章的题解教会了我每次跳两个点的遍历方法，这个方法在这道题里面过于强大了：

while(qu.size()){
		int u=qu.front(),v=fa[u];
		qu.pop();
		if(vis[v])continue;
		arr.emplace_back(v);
		vis[v]=1;
		du[fa[v]]--;
//		cout<<cur<<" ";
		if(du[fa[v]]==0){
			vis[fa[v]]=1;
			qu.push(fa[v]);
		}
	}

最重要的一点是，它解决了这样一些情况：

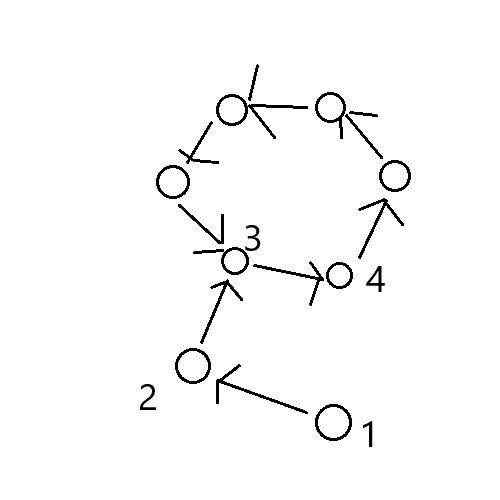
1.先假设1不存在。自然而然，2是不被圈的点，而3被圈。这种方法下在标记了2和3被访问（vis）后，还能让4的入度减少，此时4的入度为0，入队，环被拆；

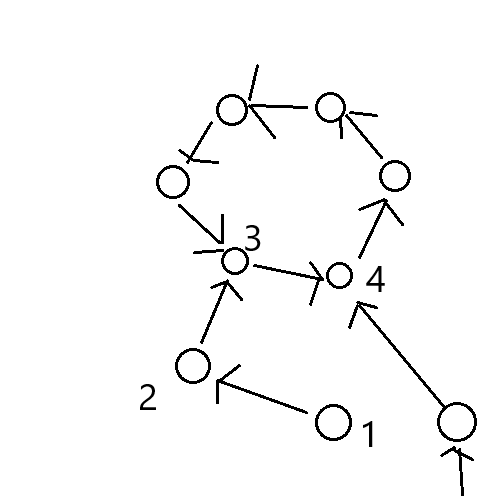
2.接着1的情况，若4入度不止环上的，还有一条更长的链，那么这个链终究会遍历到4，并且让4入队；

3.再假设1存在，则2被圈，拓扑不会拆环。但是此时3是什么对2也不会产生影响。

这些操作的结果就是，只剩下一些没有任何一个点被圈、被访问(vis)的环，就可以从任意一个点开始两个两个走（最后只能留偶环，奇数会被判别为非法）。

fff(i,1,N){
		if(vis[i]==0){
			for(int u=i;fa[u]!=u && !vis[fa[u]];u=fa[fa[u]]){
//				fa[u]!=u去除了自环
				arr.emplace_back(fa[u]);
				vis[u]=vis[fa[u]]=1;
			}
		}
	}

如果最后发现有的点没被访问，就是构造失败，-1的情况。