P3975 [TJOI2015] 弦论

原题链接 参考文章

初学SAM。第一次做SAM的题 真的很抽象…… 唐氏大学生脑子不够用了

SAM的模板来自B站的飘韵大佬

来试着描述一下我的感性理解，漏洞百出，欢迎指正。首先是后缀自动机的部分：

后缀自动机类似AC自动机，不过空间更加紧凑，设字符串长度为n，SAM的节点可以在2n个之内。

和AC自动机一样有两种边，这两种边分别是状态转移边和后缀链接，从而分别构成了一张有向无环图（DAG）和一颗树。

节点的意义是同一类endpos，它们的结束位置完全相同，同时长度连续递增，也可以说它们本质相同。反过来说，endpos不一样就代表本质不同。

关于节点，一般记录的是一个len[]，意思是这个endpos的最长子串的长度，下图中就用了最长子串来表示一个点。

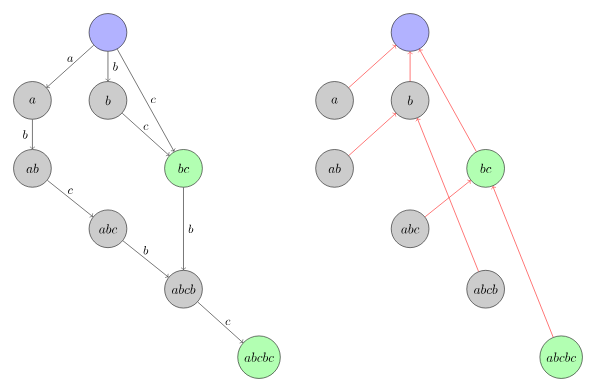
下面我们用节点的最长子串聊聊图和树的性质。

对于图，它是在父节点后加字符。和AC自动机一样，从任意节点沿着图走，就可以得到所有的子串。运用这个性质，我们可以把其他字符串放进去走，若能正常走完则表明这个字符串是原字符串的子串。

对于树，它是在父节点前面加字符。一个视角是，它是对结束位置的分割。根节点是空字符串“”，可以认为它占了所有的位置。然后每当在它前面加一个或者一些字符，一个节点的结束位置就被分割为多个子节点的结束位置。

有个性质，节点的出现次数等于它在树上的子树大小。

可以发现，图和树都是从短节点到长节点，故可以基于len[]来拓扑排序，然后用从长到短的顺序来进行树上和图上DP。这样就不会产生依赖上的问题。

然后关于这道题：

点u的贡献设为siz[u]，而从u出发能产生的串为sum[u]

对于t=0，每个点贡献只有1，也就是说每个等价类在统计上只算作1次，siz[u]=1。

而对于t==1，点的结束位置的数量也有影响，再结合上文提到的“节点的出现次数等于它在树上的子树大小”的性质，我们可以很容易地在树上统计子树大小，作为siz[u]。

还有一点，虽然根节点（下标为1，字符串为空“”）确实会算出出现次数，但因为是空串，所以两种情况siz[1]都要设为0。

之后我们可以在图上做DP，公式为：

sum[u] = siz[u] + ∑sum[ch[u][c]]

其中siz[u]是当前节点的点权，ch[u][c]是转移边。sum[u]表示从节点u出发能生成的所有子串总数，包含u自身的贡献（siz[u]）和后续转移的贡献。

其实我有个疑问：一个endpos代表的不止一个子串，这一点是不是没有考虑？然后我试着自我解答：

请看左图，根到bc节点其实是有两条路径：->b->c和->c，这两个途径就反映了不同子串的累积方式（胡言乱语）。

思路还是很混乱，希望之后的理解可以更升入。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define double long double
#define endl '\n'
// const int MAX;
// const int MOD;
// #define ll long long 
int TYP,K;
struct SAM {
	//edited by piaoyun from some other's code 
	 
	static const int MAXN=1000010,MAXS=28;
    
    int tot=1,last=1,link[MAXN << 1],ch[MAXN << 1][MAXS],len[MAXN << 1],endpos[MAXN << 1];
    int sum[MAXN<<1],A[MAXN<<1],temp[MAXN<<1];
	//总共有tot个节点，index范围是[1-tot]，初始/根节点为1 
	//last为最后一个插入的节点
	//link为后缀链接（parent树中的父节点） / 指向最长的后缀且属于不同等价类的节点
	//ch[n][s] 表示节点n通过字符s转移到的节点
	//len表示该节点代表的字符串的最长长度，注意最短的长度是 len[link[n]] + 1（父节点最长长度 + 1）
	//endpos[n] 参考get_endpos()函数，注意需要先调用该函数计算 
	void clear(){
        for(int i = 0; i <= tot; i++){
            link[i] = len[i] = endpos[i] = 0;
            for(int k = 0; k < MAXS; k++) ch[i][k] = 0;
        }
        tot=1;last=1;
    }
    
    //添加一个字符，通常为[1-26] 
    void extend(int w){
        int p=++tot,x=last,r,q;
        endpos[p]=TYP;
        for(len[last=p]=len[x]+1; x&&!ch[x][w]; x=link[x]) ch[x][w]=p;
        if(!x)link[p]=1;
        else if(len[x]+1==len[q=ch[x][w]]) link[p]=q;
        else {
            link[r=++tot]=link[q];
            memcpy(ch[r],ch[q],sizeof ch[r]);
            len[r]=len[x]+1;
            link[p]=link[q]=r;
            for(; x&&ch[x][w]==q; x=link[x])ch[x][w]=r;
        }
    }
    
    //*注意：vector会占用较多空间 
    vector<int> p[MAXN << 1]; //用于构建parent树的邻接表以便dfs 
    void dfs(int u){
    	int v;
    	for(int i=0;i<p[u].size();i++){
        	v=p[u][i];
        	dfs(v);
        	endpos[u]+=endpos[v];
   		}
	}
    
    //注意！调用该方法前endpos[]数组保存的是每个节点作为终止节点的次数
	//调用该方法后endpos[]会变为该节点代表子串在所有子串中的出现次数
    void get_endpos(){
    	for(int i = 1;i <= tot; i++) p[i].clear();
    	for(int i = 2;i <= tot; i++){
        	p[link[i]].push_back(i); //构建parent树的邻接表以便dfs 
   		}
   		dfs(1);
   		for(int i = 1;i <= tot; i++) p[i].clear();
	}
    
	void topu(){
        // 用len来进行拓扑排序 最后顺序存入A中
        // 这个顺序既可以用在后缀链接树上 也可以用在状态转移的DAG上
        // 反向遍历 即可得到len从长到短 不产生依赖冲突 的顺序
        for(int i=1;i<=tot;i++) temp[len[i]]++;
	    for(int i=1;i<=tot;i++) temp[i]+=temp[i-1];
	    for(int i=1;i<=tot;i++) A[temp[len[i]]--]=i;
    }
    void print(int x,int k){
        // x是点编号 k是递归而来的排序数
        // cout<<"p"<<endl;
        if(k<=endpos[x]){
            // cout<<-1<<endl;
            return;
        }
        k-=endpos[x];
        for(int i=1;i<=26;i++){
            if(ch[x][i]){
                if(sum[ch[x][i]]<k){
                    k-=sum[ch[x][i]];
                }else{
                    cout<<(char)(i-1+'a');
                    print(ch[x][i],k);
                    return;
                }
            }
        }
    }
	void solve(){
		//在此处实现题解的算法逻辑
		// int ans = 0;
        topu();
        // for(int i=1;i<=tot;i++){
        //     cout<<A[i]<<" ";
        // }
        // cout<<endl;
		if(TYP){
            for(int i=tot;i;i--){
                endpos[link[A[i]]]+=endpos[A[i]];
            }
            for(int i=2;i<=tot;i++)sum[i]=endpos[i];
        }else{
            for(int i=2;i<=tot;i++){
                endpos[i]=sum[i]=1;
            }
        }
        endpos[1]=sum[1]=0;
		for(int i=tot;i;i--){
            int cur=A[i];
            for(int x=1;x<=26;x++){
                if(ch[cur][x])sum[cur]+=sum[ch[cur][x]];
            }
        }
        // return ans;
	}
}sam;

string tmp;

void prepare() {
	//sam.self_test();
    // cin>>tmp;
    sam.clear();
    for(int i = 0; i < tmp.size(); i++) sam.extend(tmp[i]-'a'+1);
    // cout<<sam.solve();
}
int N,M,ans;
void solve(){
    cin>>tmp;
    cin>>TYP>>K;
    prepare();
    sam.solve();
    // cout<<111<<endl;
    if(sam.sum[1]<K){
        cout<<-1<<endl;return;
    }
    sam.print(1,K);
    cout<<endl;
}
signed main() {
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    // int times;cin>>times;
    // while(times--)
    solve();
    return 0;
}