凯利公式的应用

凯利公式代码化
凯利公式的应用代码
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
def kelly_position_size(win_probability, odds):
"""
根据凯利公式计算最优仓位比例
:param win_probability: 获胜的概率,取值范围 [0, 1]
:param odds: 赔率,即盈利与亏损的比例
:return: 最优仓位比例
"""
if odds <= 0:
return 0
# 计算失败的概率
loss_probability = 1 - win_probability
# 应用凯利公式计算最优仓位比例
# 凯利公式:f* = (bp - q)/b,其中b是赔率,p是胜率,q是败率
position_size = (odds * win_probability - loss_probability) / odds
# 确保仓位比例在合理范围 [0, 1]
position_size = max(0, min(position_size, 1))
return position_size
def simulate_returns(win_probability, odds, position_sizes, num_trades=1000, initial_capital=10000, random_seed=42):
"""
模拟不同仓位比例下的收益情况
:param win_probability: 获胜的概率
:param odds: 赔率
:param position_sizes: 要测试的仓位比例列表
:param num_trades: 模拟的交易次数
:param initial_capital: 初始资金
:param random_seed: 随机种子,确保结果可重复
:return: 每个仓位比例对应的最终资金列表
"""
# 设置随机种子以确保结果可重复
np.random.seed(random_seed)
# 预先生成所有交易的随机结果
trade_results = np.random.random(num_trades) < win_probability
final_capitals = []
position_stats = [] # 存储每个仓位的统计信息
for position_size in position_sizes:
capital = initial_capital
trades_history = [] # 记录每笔交易后的资金
for is_win in trade_results:
if is_win:
# 获胜,获得收益(考虑交易成本)
profit = capital * position_size * (odds - 1) - 0.001 * capital
capital += profit
else:
# 失败,遭受损失(考虑交易成本)
loss = capital * position_size + 0.001 * capital
capital -= loss
# 记录每笔交易后的资金
trades_history.append(capital)
# 如果资金已经归零,提前结束模拟
if capital <= 0:
print(f"警告:仓位 {position_size*100:.1f}% 在第 {len(trades_history)} 笔交易后资金归零")
break
# 计算最终资金
final_capitals.append(capital)
# 计算统计信息
if capital > 0:
returns = (capital - initial_capital) / initial_capital * 100
avg_return = returns / num_trades
max_drawdown = (min(trades_history) / initial_capital - 1) * 100
position_stats.append({
'position': position_size,
'final_capital': capital,
'returns': returns,
'avg_return': avg_return,
'max_drawdown': max_drawdown
})
return final_capitals, position_stats
def find_optimal_position(position_stats):
"""
在模拟结果中找到收益最高的仓位
:param position_stats: 仓位统计信息列表
:return: 最优仓位的统计信息
"""
if not position_stats:
return None
# 按收益率排序
optimal_stat = max(position_stats, key=lambda x: x['returns'])
return optimal_stat
def plot_position_analysis(win_probability, odds, num_trades=1000, initial_capital=10000, random_seed=42):
"""
绘制不同仓位比例下的收益分析图
"""
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 生成要测试的仓位比例
position_sizes = np.linspace(0, 1, 100)
# 计算凯利公式最优仓位
kelly_position = kelly_position_size(win_probability, odds)
# 将最优仓位添加到测试仓位列表中
if kelly_position not in position_sizes:
position_sizes = np.append(position_sizes, kelly_position)
position_sizes.sort()
# 使用相同的随机种子进行模拟
final_capitals, position_stats = simulate_returns(win_probability, odds, position_sizes, num_trades, initial_capital, random_seed)
# 计算收益率
returns = [(cap - initial_capital) / initial_capital * 100 for cap in final_capitals]
# 找到收益最高的仓位
optimal_stat = find_optimal_position(position_stats)
# 绘制图表
plt.figure(figsize=(10, 6))
plt.plot(position_sizes * 100, returns, 'b-', label='收益率')
# 标记凯利公式最优仓位
kelly_index = np.where(position_sizes == kelly_position)[0][0]
kelly_return = returns[kelly_index]
plt.plot(kelly_position * 100, kelly_return, 'ro', label='凯利公式最优仓位')
# 标记收益最高的仓位
if optimal_stat:
optimal_position = optimal_stat['position']
optimal_return = optimal_stat['returns']
plt.plot(optimal_position * 100, optimal_return, 'go', label='实际最优仓位')
plt.title(f'不同仓位比例下的收益率分析\n(胜率={win_probability:.2f}, 赔率={odds:.2f})')
plt.xlabel('仓位比例 (%)')
plt.ylabel('收益率 (%)')
plt.grid(True)
plt.legend()
plt.show()
# 输出最优仓位信息
if optimal_stat:
print(f"\n实际最优仓位比例: {optimal_stat['position'] * 100:.2f}%")
print(f"最终资金: {optimal_stat['final_capital']:,.2f}")
print(f"收益率: {optimal_stat['returns']:.2f}%")
print(f"平均每笔交易收益率: {optimal_stat['avg_return']:.2f}%")
print(f"最大回撤: {optimal_stat['max_drawdown']:.2f}%")
# 示例使用
if __name__ == "__main__":
# 设置参数
win_prob = 0.6
odds_value = 2
initial_capital = 10000
num_trades = 100 # 使用100次交易进行分析
random_seed = 42 # 设置固定的随机种子
# 计算凯利公式最优仓位
optimal_position = kelly_position_size(win_prob, odds_value)
print(f"初始资金: {initial_capital:,.2f}")
print(f"凯利公式最优仓位比例: {optimal_position * 100:.2f}% (胜率={win_prob:.2f}, 赔率={odds_value:.2f})")
# 模拟不同仓位下的收益情况
# 构建仓位列表,避免重复
base_positions = [0.1, 0.2, 0.3, 0.4, 0.5]
if optimal_position not in base_positions:
base_positions.append(optimal_position)
base_positions.sort() # 保持仓位列表有序
# 使用相同的随机种子进行模拟
final_capitals, position_stats = simulate_returns(win_prob, odds_value, base_positions, num_trades, initial_capital, random_seed)
# 打印结果
print(f"\n模拟参数: 交易次数={num_trades}, 随机种子={random_seed}")
print("\n不同仓位比例下的最终资金:")
for pos, cap in zip(base_positions, final_capitals):
return_rate = (cap - initial_capital) / initial_capital * 100
print(f"仓位比例 {pos*100:.1f}%: 最终资金 {cap:,.2f} (收益率 {return_rate:.2f}%)")
# 绘制分析图表
plot_position_analysis(win_prob, odds_value, num_trades, initial_capital, random_seed)
代码输出如下:
runfile('C:/Users/.spyder-py3未命名7.py', wdir='C:/Users/.spyder-py3/')
初始资金: 10,000.00
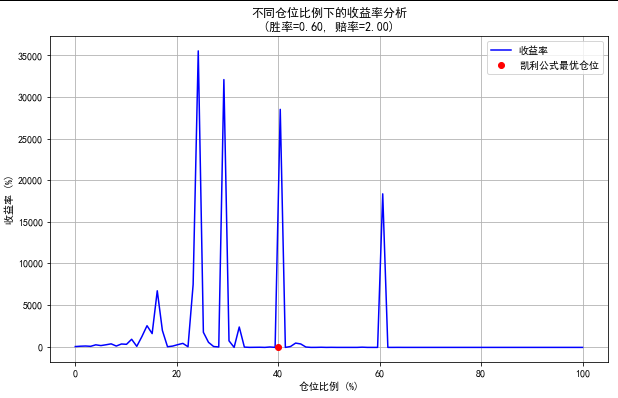
凯利公式最优仓位比例: 40.00% (胜率=0.60, 赔率=2.00)
模拟参数: 交易次数=100, 随机种子=42
不同仓位比例下的最终资金:
仓位比例 10.0%: 最终资金 74,466.89 (收益率 644.67%)
仓位比例 20.0%: 最终资金 229,002.05 (收益率 2190.02%)
仓位比例 30.0%: 最终资金 252,948.45 (收益率 2429.48%)
仓位比例 40.0%: 最终资金 89,394.01 (收益率 793.94%)
仓位比例 40.0%: 最终资金 89,394.01 (收益率 793.94%)
仓位比例 50.0%: 最终资金 8,039.39 (收益率 -19.61%)
警告:仓位 100.0% 在第 2 笔交易后资金归零
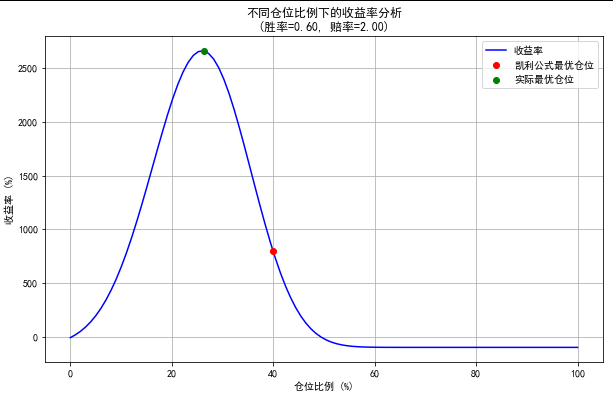
实际最优仓位比例: 26.26%
最终资金: 276,230.85
收益率: 2662.31%
平均每笔交易收益率: 26.62%
最大回撤: -52.66%
疑问1:
上述代码计算出来的凯利公式计算的最优仓位和实际模拟中找到的最优仓位不同,是什么原因导致的?这能证明凯利公式失效了?还是有其他隐藏的因素我们没有考虑到位
DS回答:
凯利公式计算的最优仓位和实际模拟中找到的最优仓位不同,并不一定意味着凯利公式失效,而是可能由以下原因导致的。我们需要仔细分析这些原因,并判断是否需要进一步优化模型或调整参数。
- 凯利公式的假设与实际模拟的差异
凯利公式基于一些理想化的假设,而实际模拟中可能存在以下差异:
1.1 凯利公式的假设
无限次重复:凯利公式假设投资是无限次重复的,而实际模拟中交易次数是有限的(如100次)。
固定胜率和赔率:凯利公式假设胜率和赔率是固定不变的,而实际市场中胜率和赔率可能会波动。
无交易成本:凯利公式没有考虑交易成本(如手续费、滑点等),而实际交易中这些成本会影响收益。
1.2 实际模拟的差异
有限次交易:在有限次交易中,随机性可能导致实际收益偏离理论预期。
资金归零风险:在实际模拟中,如果仓位过高,资金可能会在交易过程中归零,导致无法继续交易。
随机性影响:即使胜率和赔率固定,随机性也可能导致实际收益与理论收益不一致。
- 导致差异的具体原因
2.1 交易次数不足
问题:如果交易次数较少(如100次),随机性可能导致实际收益偏离理论预期。
解决方案:增加交易次数(如1000次或更多),以减少随机性的影响。
2.2 资金归零风险
问题:如果仓位过高,资金可能在交易过程中归零,导致无法继续交易。
解决方案:在模拟中增加对资金归零的处理逻辑,并确保仓位比例不会过高。
2.3 模型参数不准确
问题:如果输入的胜率或赔率不准确,凯利公式计算的最优仓位也会不准确。
解决方案:确保输入的胜率和赔率是基于实际数据或合理估计的。
2.4 未考虑交易成本
问题:实际交易中存在交易成本(如手续费、滑点等),而凯利公式没有考虑这些成本。
解决方案:在模拟中加入交易成本,调整仓位比例。
- 改进方案
为了减少凯利公式最优仓位与实际最优仓位的差异,我们可以对模型进行以下改进:
3.1 增加交易次数
将交易次数从100次增加到1000次或更多,以减少随机性的影响。
3.2 增加资金归零处理
在模拟中增加对资金归零的处理逻辑,确保仓位比例不会过高。
修改代码:
if capital <= 0:
print(f"警告:仓位 {position_size*100:.1f}% 在第 {len(trades_history)} 笔交易后资金归零")
break
3.3 调整模型参数
确保输入的胜率和赔率是基于实际数据或合理估计的。
如果胜率或赔率不准确,重新估计这些参数。
3.4 加入交易成本
在模拟中加入交易成本(如手续费、滑点等),调整仓位比例。
修改代码:
transaction_cost = 0.001 # 假设每次交易的成本为0.1%
if is_win:
profit = capital * position_size * (odds - 1) - transaction_cost * capital
capital += profit
else:
loss = capital * position_size + transaction_cost * capital
capital -= loss
- 验证凯利公式的有效性
4.1 理论验证
凯利公式在理论上是最优的,但在实际应用中需要满足其假设条件(如无限次重复、固定胜率和赔率等)。
如果实际条件与假设条件不符,凯利公式的最优仓位可能会偏离实际最优仓位。
4.2 实际验证
通过改进模型(如增加交易次数、加入交易成本等),可以减少凯利公式最优仓位与实际最优仓位的差异。
如果改进后差异仍然较大,可能需要重新评估模型参数或考虑其他因素(如市场波动、心理因素等)。
代码改进
以下是改进后的代码示例:
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
def kelly_position_size(win_probability, odds):
"""
根据凯利公式计算最优仓位比例
:param win_probability: 获胜的概率,取值范围 [0, 1]
:param odds: 赔率,即盈利与亏损的比例
:return: 最优仓位比例
"""
if odds <= 0:
return 0
# 计算失败的概率
loss_probability = 1 - win_probability
# 应用凯利公式计算最优仓位比例
# 凯利公式:f* = (bp - q)/b,其中b是赔率,p是胜率,q是败率
position_size = (odds * win_probability - loss_probability) / odds
# 确保仓位比例在合理范围 [0, 1]
position_size = max(0, min(position_size, 1))
return position_size
def simulate_returns(win_probability, odds, position_sizes, num_trades=1000, initial_capital=10000, random_seed=42, fee_rate=0.001):
"""
模拟不同仓位比例下的收益情况
:param win_probability: 获胜的概率
:param odds: 赔率
:param position_sizes: 要测试的仓位比例列表
:param num_trades: 模拟的交易次数
:param initial_capital: 初始资金
:param random_seed: 随机种子,确保结果可重复
:param fee_rate: 手续费率
:return: 每个仓位比例对应的最终资金列表
"""
# 设置随机种子以确保结果可重复
np.random.seed(random_seed)
# 预先生成所有交易的随机结果
trade_results = np.random.random(num_trades) < win_probability
final_capitals = []
position_stats = [] # 存储每个仓位的统计信息
for position_size in position_sizes:
capital = initial_capital
trades_history = [] # 记录每笔交易后的资金
for is_win in trade_results:
if is_win:
# 获胜,获得收益(考虑交易成本)
profit = capital * position_size * (odds - 1) - fee_rate * capital
capital += profit
else:
# 失败,遭受损失(考虑交易成本)
loss = capital * position_size + fee_rate * capital
capital -= loss
# 记录每笔交易后的资金
trades_history.append(capital)
# 如果资金已经归零,提前结束模拟
if capital <= 0:
print(f"警告:仓位 {position_size*100:.1f}% 在第 {len(trades_history)} 笔交易后资金归零")
break
# 计算最终资金
final_capitals.append(capital)
# 计算统计信息
if capital > 0:
returns = (capital - initial_capital) / initial_capital * 100
avg_return = returns / num_trades
max_drawdown = (min(trades_history) / initial_capital - 1) * 100
position_stats.append({
'position': position_size,
'final_capital': capital,
'returns': returns,
'avg_return': avg_return,
'max_drawdown': max_drawdown
})
return final_capitals, position_stats
def find_optimal_position(position_stats):
"""
在模拟结果中找到收益最高的仓位
:param position_stats: 仓位统计信息列表
:return: 最优仓位的统计信息
"""
if not position_stats:
return None
# 按收益率排序
optimal_stat = max(position_stats, key=lambda x: x['returns'])
return optimal_stat
def plot_position_analysis(win_probability, odds, num_trades=1000, initial_capital=10000, random_seed=42, fee_rate=0.001):
"""
绘制不同仓位比例下的收益分析图
"""
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 生成要测试的仓位比例
position_sizes = np.linspace(0, 1, 100)
# 计算凯利公式最优仓位
kelly_position = kelly_position_size(win_probability, odds)
# 将最优仓位添加到测试仓位列表中
if kelly_position not in position_sizes:
position_sizes = np.append(position_sizes, kelly_position)
position_sizes.sort()
# 使用相同的随机种子进行模拟
final_capitals, position_stats = simulate_returns(win_probability, odds, position_sizes, num_trades, initial_capital, random_seed, fee_rate)
# 计算收益率
returns = [(cap - initial_capital) / initial_capital * 100 for cap in final_capitals]
# 找到收益最高的仓位
optimal_stat = find_optimal_position(position_stats)
# 绘制图表
plt.figure(figsize=(10, 6))
plt.plot(position_sizes * 100, returns, 'b-', label='收益率')
# 标记凯利公式最优仓位
kelly_index = np.where(position_sizes == kelly_position)[0][0]
kelly_return = returns[kelly_index]
plt.plot(kelly_position * 100, kelly_return, 'ro', label='凯利公式最优仓位')
# 标记收益最高的仓位
if optimal_stat:
optimal_position = optimal_stat['position']
optimal_return = optimal_stat['returns']
plt.plot(optimal_position * 100, optimal_return, 'go', label='实际最优仓位')
plt.title(f'不同仓位比例下的收益率分析\n(胜率={win_probability:.2f}, 赔率={odds:.2f})')
plt.xlabel('仓位比例 (%)')
plt.ylabel('收益率 (%)')
plt.grid(True)
plt.legend()
plt.show()
# 输出最优仓位信息
if optimal_stat:
print(f"\n实际最优仓位比例: {optimal_stat['position'] * 100:.2f}%")
print(f"最终资金: {optimal_stat['final_capital']:,.2f}")
print(f"收益率: {optimal_stat['returns']:.2f}%")
print(f"平均每笔交易收益率: {optimal_stat['avg_return']:.2f}%")
print(f"最大回撤: {optimal_stat['max_drawdown']:.2f}%")
def run_kelly_analysis(win_probability, odds, num_trades=1000, initial_capital=10000, random_seed=42, fee_rate=0.001, base_positions=None):
"""
运行凯利公式分析并输出结果
"""
if base_positions is None:
base_positions = [0.1, 0.2, 0.3, 0.4, 0.5]
# 计算凯利公式最优仓位
optimal_position = kelly_position_size(win_probability, odds)
print(f"初始资金: {initial_capital:,.2f}")
print(f"凯利公式最优仓位比例: {optimal_position * 100:.2f}% (胜率={win_probability:.2f}, 赔率={odds:.2f})")
# 构建仓位列表,避免重复
if optimal_position not in base_positions:
base_positions.append(optimal_position)
base_positions.sort() # 保持仓位列表有序
# 使用相同的随机种子进行模拟
final_capitals, position_stats = simulate_returns(win_probability, odds, base_positions, num_trades, initial_capital, random_seed, fee_rate)
# 打印结果
print(f"\n模拟参数: 交易次数={num_trades}, 随机种子={random_seed}, 手续费率={fee_rate:.2%}")
print("\n不同仓位比例下的最终资金:")
for pos, cap in zip(base_positions, final_capitals):
return_rate = (cap - initial_capital) / initial_capital * 100
print(f"仓位比例 {pos*100:.1f}%: 最终资金 {cap:,.2f} (收益率 {return_rate:.2f}%)")
# 绘制分析图表
plot_position_analysis(win_probability, odds, num_trades, initial_capital, random_seed, fee_rate)
# 示例使用
if __name__ == "__main__":
# 设置参数
win_prob = 0.6
odds_value = 2
initial_capital = 10000
num_trades = 100 # 使用100次交易进行分析
random_seed = 42 # 设置固定的随机种子
fee_rate = 0.001 # 手续费率
# 调用函数进行分析
run_kelly_analysis(win_prob, odds_value, num_trades, initial_capital, random_seed, fee_rate)
输出结果:
初始资金: 10,000.00
凯利公式最优仓位比例: 40.00% (胜率=0.60, 赔率=2.00)
模拟参数: 交易次数=100, 随机种子=42, 手续费率=0.10%
不同仓位比例下的最终资金:
仓位比例 10.0%: 最终资金 74,466.89 (收益率 644.67%)
仓位比例 20.0%: 最终资金 229,002.05 (收益率 2190.02%)
仓位比例 30.0%: 最终资金 252,948.45 (收益率 2429.48%)
仓位比例 40.0%: 最终资金 89,394.01 (收益率 793.94%)
仓位比例 40.0%: 最终资金 89,394.01 (收益率 793.94%)
仓位比例 50.0%: 最终资金 8,039.39 (收益率 -19.61%)
警告:仓位 100.0% 在第 2 笔交易后资金归零
实际最优仓位比例: 26.26%
- 总结
凯利公式计算的最优仓位与实际模拟中的最优仓位不同,可能是由于交易次数不足、资金归零风险、模型参数不准确或未考虑交易成本等原因导致的。
通过改进模型(如增加交易次数、加入交易成本等),可以减少这种差异。
凯利公式在理论上是最优的,但在实际应用中需要满足其假设条件。如果实际条件与假设条件不符,可能需要重新评估模型参数或考虑其他因素。
疑问2:
如上所述,凯利公式计算的最优仓位40%与实际模拟中的最优仓位20%-30%不同,带给交易者什么样的启示?在实际交易中应如何应用?请举例说明具体的方法
凯利公式计算的最优仓位(如40%)与实际模拟中的最优仓位(如20%-30%)不同,这为交易者提供了重要的启示。以下是具体的分析和实际应用建议:
- 凯利公式的启示
1.1 理论最优与实际最优的差异
理论最优:凯利公式基于无限次重复和固定胜率、赔率的假设,计算出理论上的最优仓位(如40%)。
实际最优:在实际交易中,由于交易次数有限、资金归零风险、交易成本等因素,实际最优仓位可能低于理论最优仓位(如20%-30%)。
1.2 风险与收益的平衡
高风险:凯利公式的最优仓位可能过高,导致资金归零风险增加。
稳健性:实际最优仓位较低,能够在保证收益的同时降低风险。
- 实际应用建议
在实际交易中,交易者可以结合凯利公式的理论最优仓位和实际模拟结果,采取以下方法:
2.1 使用凯利公式的“部分仓位”
方法:将凯利公式计算的最优仓位(如40%)乘以一个“风险系数”(如0.5),得到实际仓位(如20%)。
优点:降低资金归零风险,同时保持较高的收益。
示例:
凯利公式最优仓位:40%。
风险系数:0.5。
实际仓位:40% * 0.5 = 20%。
2.2 动态调整仓位
方法:根据市场条件和账户资金动态调整仓位。
当账户资金增加时,适当提高仓位。
当账户资金减少时,适当降低仓位。
优点:避免过度冒险,保持稳健性。
示例:
初始仓位:20%。
账户资金增长10%后,仓位调整为22%。
账户资金减少10%后,仓位调整为18%。
2.3 结合模拟结果优化仓位
方法:通过实际模拟找到最优仓位范围(如20%-30%),并在此范围内选择具体仓位。
优点:基于实际数据优化仓位,降低风险。
示例:
模拟结果显示最优仓位范围为20%-30%。
选择具体仓位:25%。
2.4 设置止损和止盈
方法:为每笔交易设置止损和止盈,控制单笔交易的风险。
优点:避免单笔交易对账户资金造成过大影响。
示例:
止损:2%。
止盈:5%。
- 具体应用示例
假设交易者使用凯利公式和实际模拟结果进行交易,具体步骤如下:
3.1 计算凯利公式最优仓位
胜率(p):60%。
赔率(b):2。
凯利公式最优仓位:
python
复制
f* = (bp - q) / b = (2 * 0.6 - 0.4) / 2 = 0.4 (40%)
3.2 使用“部分仓位”
风险系数:0.5。
实际仓位:40% * 0.5 = 20%。
3.3 动态调整仓位
初始仓位:20%。
账户资金增长10%后,仓位调整为22%。
账户资金减少10%后,仓位调整为18%。
3.4 设置止损和止盈
止损:2%。
止盈:5%。
3.5 实际交易
每笔交易使用20%的仓位。
如果账户资金增长10%,将仓位提高到22%。
如果账户资金减少10%,将仓位降低到18%。
每笔交易设置2%的止损和5%的止盈。
- 总结
启示:凯利公式的最优仓位可能过高,实际交易中应结合模拟结果和风险控制,选择更稳健的仓位。
应用方法:
使用凯利公式的“部分仓位”(如40% * 0.5 = 20%)。
动态调整仓位,根据账户资金变化灵活调整。
结合模拟结果优化仓位,选择最优范围(如20%-30%)。
设置止损和止盈,控制单笔交易的风险。
通过以上方法,交易者可以在保证收益的同时降低风险,实现稳健的交易策略。
以上内容仅供研究使用,不作为投资建议




 浙公网安备 33010602011771号
浙公网安备 33010602011771号