Z检验和t检验的运用--趣味例子--打麻将概率分析
主要内容:Z检验和t检验的PYTHON实现和分析,比如我们随便伪造一份数据,打麻将的日期以及输赢,数据长这样子。
play为1则是打了麻将,并记录输赢;
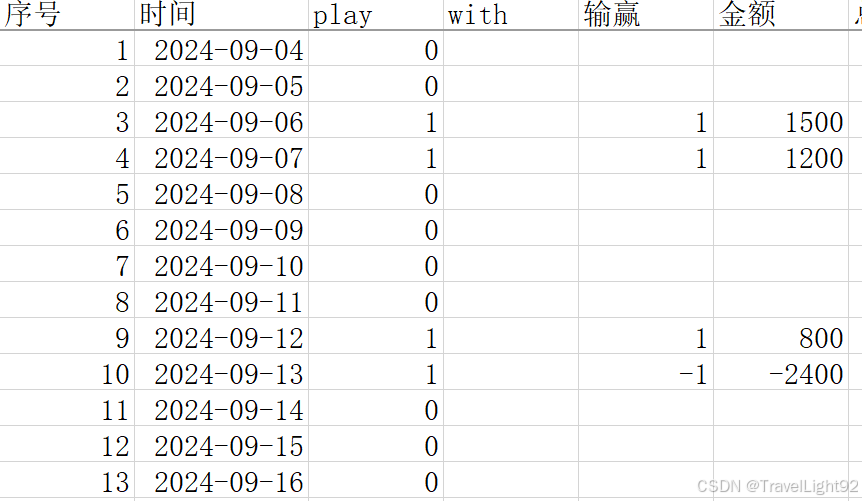
假设一个人,自称只是周末打打麻将,那么一年下来,打麻将的概率约为28.8%;
但经过一段时间的观察和记录,发现打麻将的概率明显不止这些,那么我们如何确定,他/她是否在说谎;
1.创建数据:
首先我们把2023年的周一到周五设为0,周六周日设为1,作为对照组;
import numpy as np
import pandas as pd
import datetime
temp_dates = pd.date_range("2023-01-01","2023-12-31",freq='D')
# temp_dates
def get_it(da):
return 1 if da.weekday() == 5 or da.weekday() == 6 else 0
temp_df = pd.DataFrame({'date':temp_dates})
# dodo是随便起的列名周末为1,其余时间为0
temp_df['dodo'] = list(map(get_it,temp_dates))
temp_df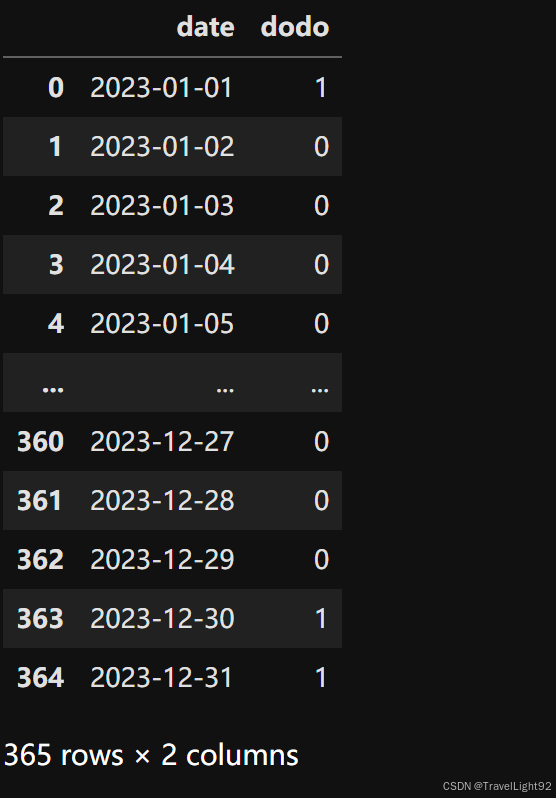
如下,这样算下来,概率就是28.8%这样子;
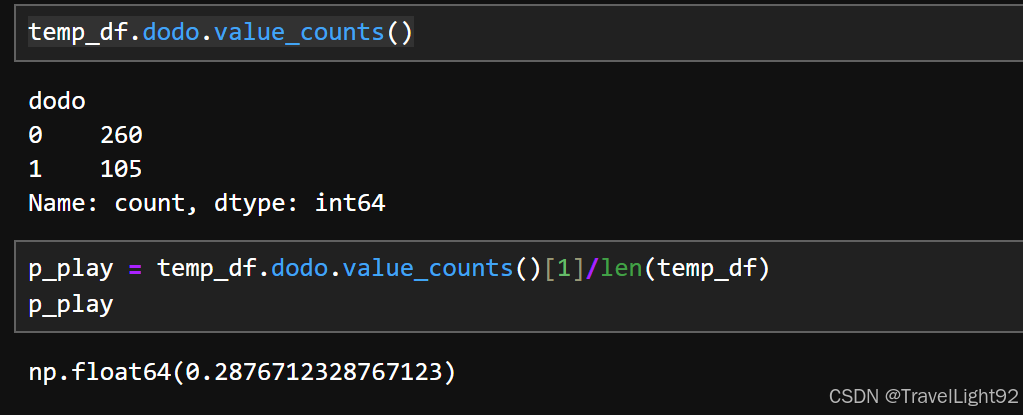
由于很多实现假设检验的库,需要一个列表或者数组,我们就弄出来;
# 2023年伪造的数据
raw_data = temp_df.dodo.values
# 近期观察记录的数据
new_data=df.values.ravel()
new_data 也就是42天打了17次麻将,概率为41.4%;
也就是42天打了17次麻将,概率为41.4%;
2.计算均值标准差
# 只是周末打牌的
mean_raw = np.mean(raw_data)
std_raw = np.std(raw_data)
print('源数据均值:',mean_raw,'源数据标准误差:',std_raw)
# 近期观察的
mean_new = np.mean(new_data)
std_new= np.std(new_data)
print('近期数据均值:',mean_new,'近期数据标准误差:',std_new)
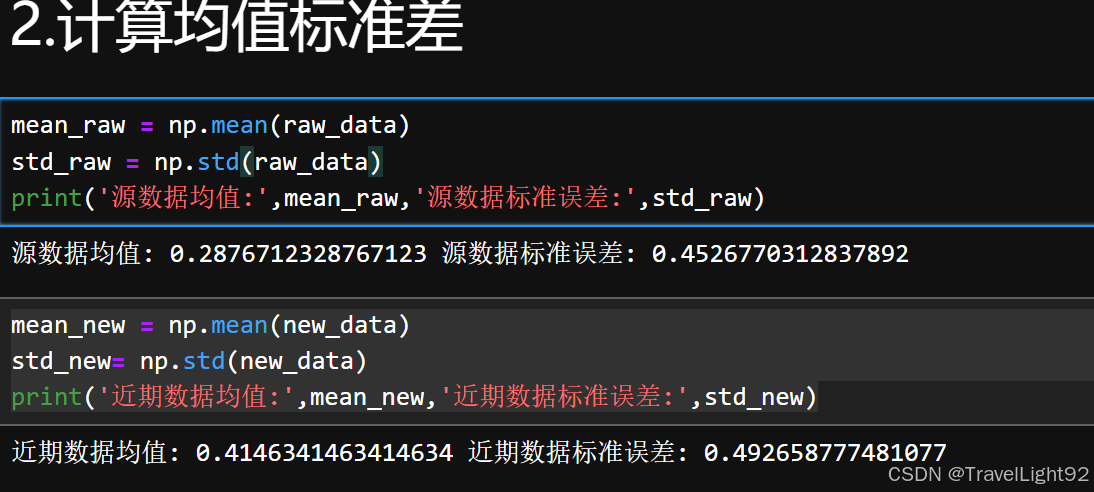
注意numpy计算的时候,ddof自由度为0,即除以n而不是n-1;
3.尝试Z检验
假如,我们要确认,打牌概率是否从周末打(28.8%)上升到近期观察的(41.4%),需要一定的样本量,我们看看42天的观察记录是否达到要求,若是样本量过少,则容易犯取伪错误;
3.1样本量的要求
而样本量的选择,依赖几个参数;
# 如果用Z检验,最小样本量
# 取alpha或0.05;beta为20%;
z_alpha = norm.ppf(0.95)
z_beta = norm.ppf(0.8)
# z_beta,z_alpha
d = mean_new-2/7 # 均值之差
n_least_z = ((z_alpha+z_beta)*std_raw/d)**2
n_least_z
# np.float64(76.22639987239985)shit!居然还不够数,就像摇骰子,每个骰子的概率为1/6,但还是可以摇到五个一,有可能只是近期发生得过于频繁而已;但是弃真错误,不依赖样本量,依然可以强搞!
3.2 双尾检验,均值是否有差异
# 双边检验--双样本方差相同
# 看近期数据,是否和2/7的概率有明显差异
import statsmodels.stats.weightstats as sw
z,p = sw.ztest(raw_data,new_data,alternative='two-sided',usevar='pooled')
print(z)
print(p)
-1.682999425881847
0.09237520256460527淦,9.2%,很难完全拒绝原假设,无法从统计学上定死,概率变化了;
双尾检验要求比较严格嘛,我们可以用单尾;
3.3 单尾检验
原假设:七分之二的概率大于等于近期打牌概率
备择假设:近期打牌概率大于2/7(这是我们希望通过反证法验证的结果)
import statsmodels.stats.weightstats as sw
z,p = sw.ztest(raw_data,new_data,alternative='smaller')
print(z)
print(p)
-1.682999425881847
0.046187601282302634这下好了,低于5%,可以拒绝原假设,认为raw_data 是小于new_data的均值的,即确认,经过一段时间的观察,打牌的概率根本不止2/7,要高一些的;不过,我们样本量不够,容易犯取伪错误;
3.4 找上下限
虽然近期打牌的概率为41.4%,但我可以自称只是近期比较频繁,平时是坚决不打麻将的;亦或者在麻将圈中,别人说你怎么最近没怎么打麻将,我可以自称近期比较忙,我平时绝对不会只打这么少次数的,即确定上下限,我们循环查找;
找下限:
result_df = pd.DataFrame()
index=1
pd.set_option('display.max_rows',None)
for i in np.arange(0.1,1,0.01):
z,p = sw.ztest(new_data,value=i,alternative='larger')
result_df.loc[index,'打牌概率'] = i
result_df.loc[index,'Z值'] = z
result_df.loc[index,'p值'] = p
index+=1
# 看起来聪明一点的办法找到临界值
rate_down = result_df[result_df['p值']>=0.05].head(1)['打牌概率'].values
rate_down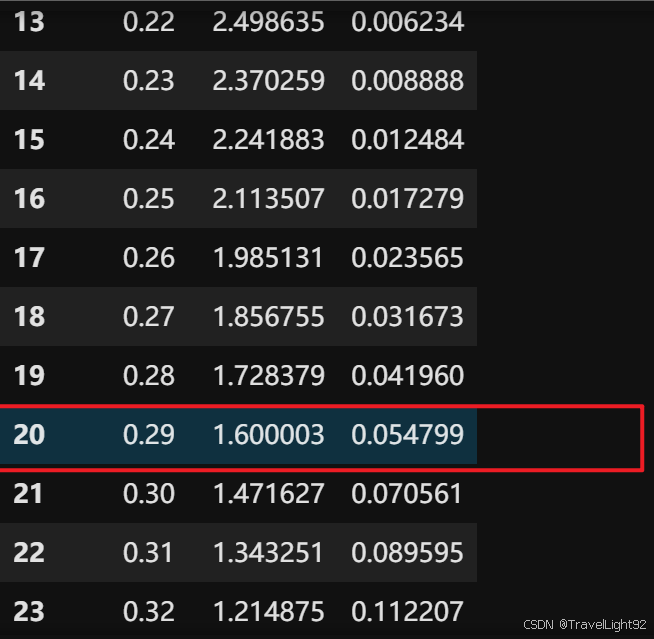
同理找到上限:
pd.set_option('display.float_format', lambda x: '%.4f' % x) # 4位小数
result_df2 = pd.DataFrame()
index=1
pd.set_option('display.max_rows',None)
for i in np.arange(0.1,1,0.01):
z,p = sw.ztest(new_data,value=i,alternative='smaller')
result_df2.loc[index,'打牌概率'] = i
result_df2.loc[index,'Z值'] = z
result_df2.loc[index,'p值'] = p
index+=1
result_df2rate_ceil = result_df2[result_df2['p值']>=0.05].tail(1).打牌概率.values
rate_ceil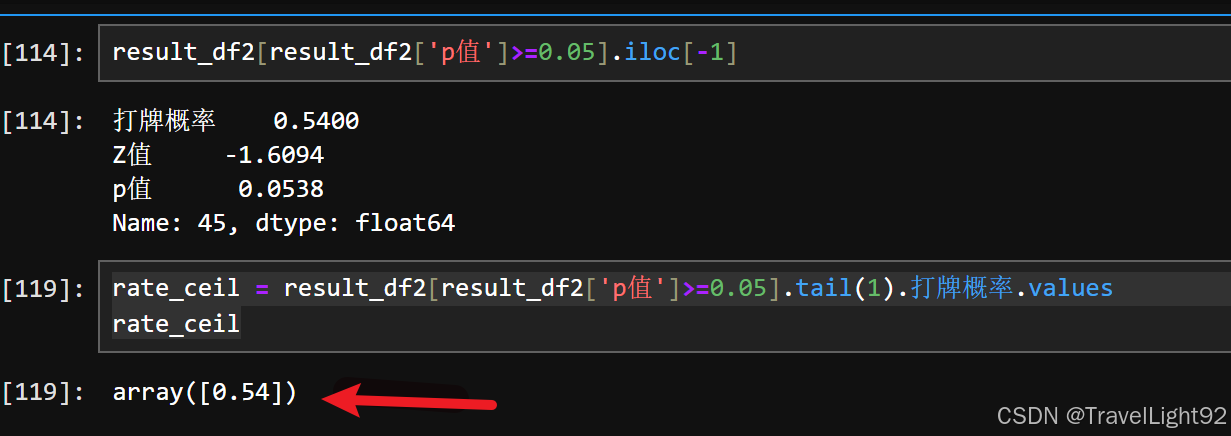
4.t检验
一般地认为,Z检验要求总体正态分布,并且样本量大于30,但这基本是个经验之谈,很多软件或者代码的内部实现,依然是T检验;
4.1 样本量要求
T检验的样本量,跟alpha,beta和均值之差除以样本标准差有关,此处可计算
delta = np.abs(mean_new-mean_raw)/std_raw
delta # np.float64(0.28047129562700596)查表可知,约需要71个,还是不符合要求,不过观察太麻烦,就这样了;
下面的流程同Z检验,不过调用的库不同;
4.2 均值是否有差异
tstat, pval = stats.ttest_ind(a=raw_data, b=new_data, alternative="two-sided")
print("t-stat: {:.2f} pval: {:.4f}".format(tstat, pval))
# 双边检验证明差异性
t-stat: -1.68 pval: 0.0931还是要接受原假设;
tstat, pval = stats.ttest_ind(a=raw_data, b=new_data, alternative="less")
print("t-stat: {:.2f} pval: {:.4f}".format(tstat, pval))
# 拒绝原假设,认为近期数据大于2/7
t-stat: -1.68 pval: 0.04664.3 找下限
result_df3 = pd.DataFrame()
index=1
for rate in np.arange(0.1,0.8,0.01):
t_stat, t_pval = stats.ttest_1samp(a=new_data, popmean=rate, alternative='greater')
result_df3.loc[index,'rate']=rate
result_df3.loc[index,'t_stat']=t_stat
result_df3.loc[index,'pval']=t_pval
index+=1
rate_down_t = result_df3[result_df3['pval']>=0.05].iloc[0]['rate']
rate_down_t结果同Z,29%,因为我这分的比较粗旷,Z和T计算公式不同,小数点再精确一位,估计就能看出差异了;
4.4 找上限
result_df4 = pd.DataFrame()
index=1
for rate in np.arange(0.1,0.8,0.01):
t_stat, t_pval = stats.ttest_1samp(a=new_data, popmean=rate, alternative='less')
result_df4.loc[index,'rate']=rate
result_df4.loc[index,'t_stat']=t_stat
result_df4.loc[index,'pval']=t_pval
index+=1
rate_ceil_t = result_df4[result_df4['pval']>=0.05].iloc[-1]['rate']
rate_ceil_t结果同Z,54%;
5.我们将代码封装一下,同时添加一些图表功能
数据较之前增加了一些,因为这个类是我后来修改文章补充的内容;
import numpy as np
import pandas as pd
import datetime
from scipy.stats import norm
import matplotlib.pyplot as plt
import statsmodels.stats.weightstats as sw
import math
from scipy import stats
# 创建一年中周六周日为1的数据
class DaMajiang(object):
def __init__(self, path="D:\打麻将记录.xlsx", raw_data=None, use_z=True, use_t=True, if_draw=True, alpha=0.05,
beta=0.2):
self.path = path
self.alpha = alpha
self.beta = beta
self.use_z = use_z
self.use_t = use_t
self.if_draw = if_draw
if not raw_data:
"生成2023年周六周日为1其余为0的打麻将数据"
temp_dates = pd.date_range("2023-01-01", "2023-12-31", freq='D')
def get_it(da):
return 1 if da.weekday() == 5 or da.weekday() == 6 else 0
temp_df = pd.DataFrame({'date': temp_dates})
# dodo是随便起的列名周末为1,其余时间为0
temp_df['dodo'] = list(map(get_it, temp_dates))
self.raw_rate = temp_df.dodo.value_counts()[1] / len(temp_df)
self.raw_data = temp_df.dodo.values
temp = pd.read_excel(self.path, sheet_name="Sheet1", dtype={'play': int}, usecols='C')
self.new_data = temp.values.ravel()
if raw_data:
self.raw_data = raw_data
self.raw_rate = np.mean(self.raw_data)
def calculate_info(self):
self.mean_raw = np.mean(self.raw_data) # 假设历史数据均值
self.std_raw = np.std(self.raw_data) # 假设历史数据标准差
self.mean_new = np.mean(self.new_data) # 近期数据均值
self.std_new = np.std(self.new_data) # 近期数据标准差
def try_z(self):
delta = np.abs(self.mean_new - self.mean_raw)
z_alpha = norm.ppf(1 - self.alpha)
z_beta = norm.ppf(1 - self.beta)
n_least_z = ((z_alpha + z_beta) * self.std_raw / delta) ** 2
print("不犯取伪错误的情况下,样本量至少要", math.ceil(n_least_z), "个")
print("目前采集的样本数", len(self.new_data))
# 双样本同方差,双边检验
print('----运用Z检验进行验证----')
print("----开始验证近期打牌概率,与之前是否相同----")
z, p = sw.ztest(self.raw_data, self.new_data, alternative='two-sided', usevar='pooled')
print("z-test:", z, "p-value:", p)
print(f"原本假设周六周日打牌,根据近期观察的情况判断,在假设历史打牌概率为{round(self.raw_rate, 2)}的情况下")
print('经过观察记录近期打牌的次数,这一系列事件的发生概率为', round(p, 4))
if p < self.alpha:
print("结论----拒绝原假设,近期数据的均值与假设历史数据的均值不同----")
else:
print("结论----接受原假设,近期数据的均值与假设历史数据的均值相同----")
# 单边检验找下限
result_df = pd.DataFrame()
index = 1
for i in np.arange(0.1, 1, 0.01):
z, p = sw.ztest(self.new_data, value=i, alternative='larger')
result_df.loc[index, '打牌概率'] = i
result_df.loc[index, 'Z值'] = z
result_df.loc[index, 'p值'] = p
index += 1
rate_down = result_df[result_df['p值'] >= 0.05].head(1)['打牌概率'].values
print("打牌概率下限:", round(rate_down[0], 2))
# 单边检验找上限
result_df2 = pd.DataFrame()
index_2 = 1
pd.set_option('display.max_rows', 20)
for i in np.arange(0.1, 1, 0.01):
z, p = sw.ztest(self.new_data, value=i, alternative='smaller')
result_df2.loc[index_2, '打牌概率'] = i
result_df2.loc[index_2, 'Z值'] = z
result_df2.loc[index_2, 'p值'] = p
index_2 += 1
rate_ceil = result_df2[result_df2['p值'] >= 0.05].tail(1).打牌概率.values
print("打牌概率上限:", round(rate_ceil[0], 2))
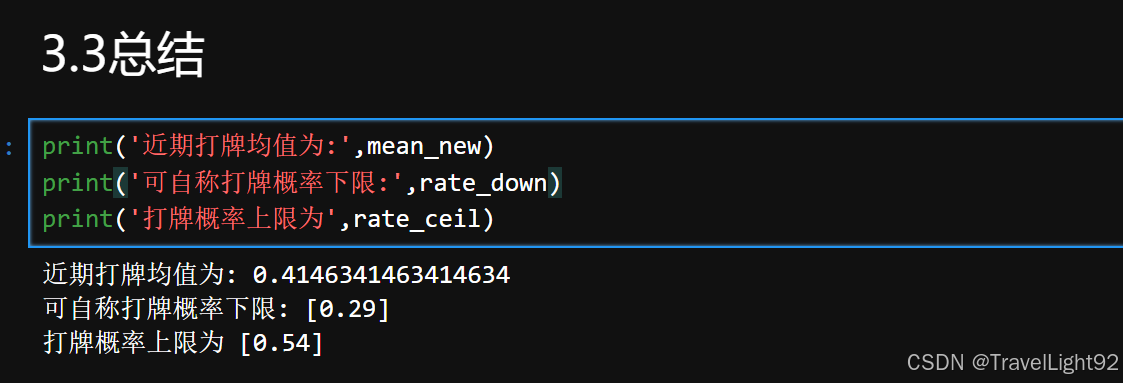
print('近期打牌均值为:', self.mean_new)
# print('可自称打牌概率下限:', round(rate_down[0],2))
# print('可自称打牌概率上限为', round(rate_ceil[0],2))
def try_t(self):
# 双样本独立,双侧检验
print('-' * 50)
print('----运用T检验进行验证----')
print('验证近期数据是否与往期数据发生改变')
tstat, pval = stats.ttest_ind(a=self.raw_data, b=self.new_data, alternative="two-sided")
print("t-test:", tstat, "p-value:", pval)
print(f"原本假设周六周日打牌,根据近期观察的情况判断,在假设历史打牌概率为{round(self.raw_rate, 2)}的情况下")
print('经过观察记录近期打牌的次数,这一系列事件的发生概率为', round(pval, 4))
if pval < self.alpha:
print("结论----拒绝原假设,近期数据的均值与假设历史数据的均值不同----")
else:
print("结论----接受原假设,近期数据的均值与假设历史数据的均值相同----")
# 单边检验找下限
result_df3 = pd.DataFrame()
index = 1
for rate in np.arange(0.1, 1, 0.01):
t_stat, t_pval = stats.ttest_1samp(a=self.new_data, popmean=rate, alternative='greater')
result_df3.loc[index, 'rate'] = rate
result_df3.loc[index, 't_stat'] = t_stat
result_df3.loc[index, 'pval'] = t_pval
index += 1
rate_down_t = result_df3[result_df3['pval'] >= 0.05].iloc[0]['rate']
print("T检验打牌概率下限:", round(rate_down_t, 2))
# 单边检验找上限
result_df4 = pd.DataFrame()
index_2 = 1
for rate in np.arange(0.1, 1, 0.01):
t_stat, t_pval = stats.ttest_1samp(a=self.new_data, popmean=rate, alternative='less')
result_df4.loc[index_2, 'rate'] = rate
result_df4.loc[index_2, 't_stat'] = t_stat
result_df4.loc[index_2, 'pval'] = t_pval
index_2 += 1
rate_ceil_t = result_df4[result_df4['pval'] >= 0.05].iloc[-1]['rate']
print("T检验打牌概率上限:", round(rate_ceil_t, 2))
print('近期打牌均值为:', self.mean_new)
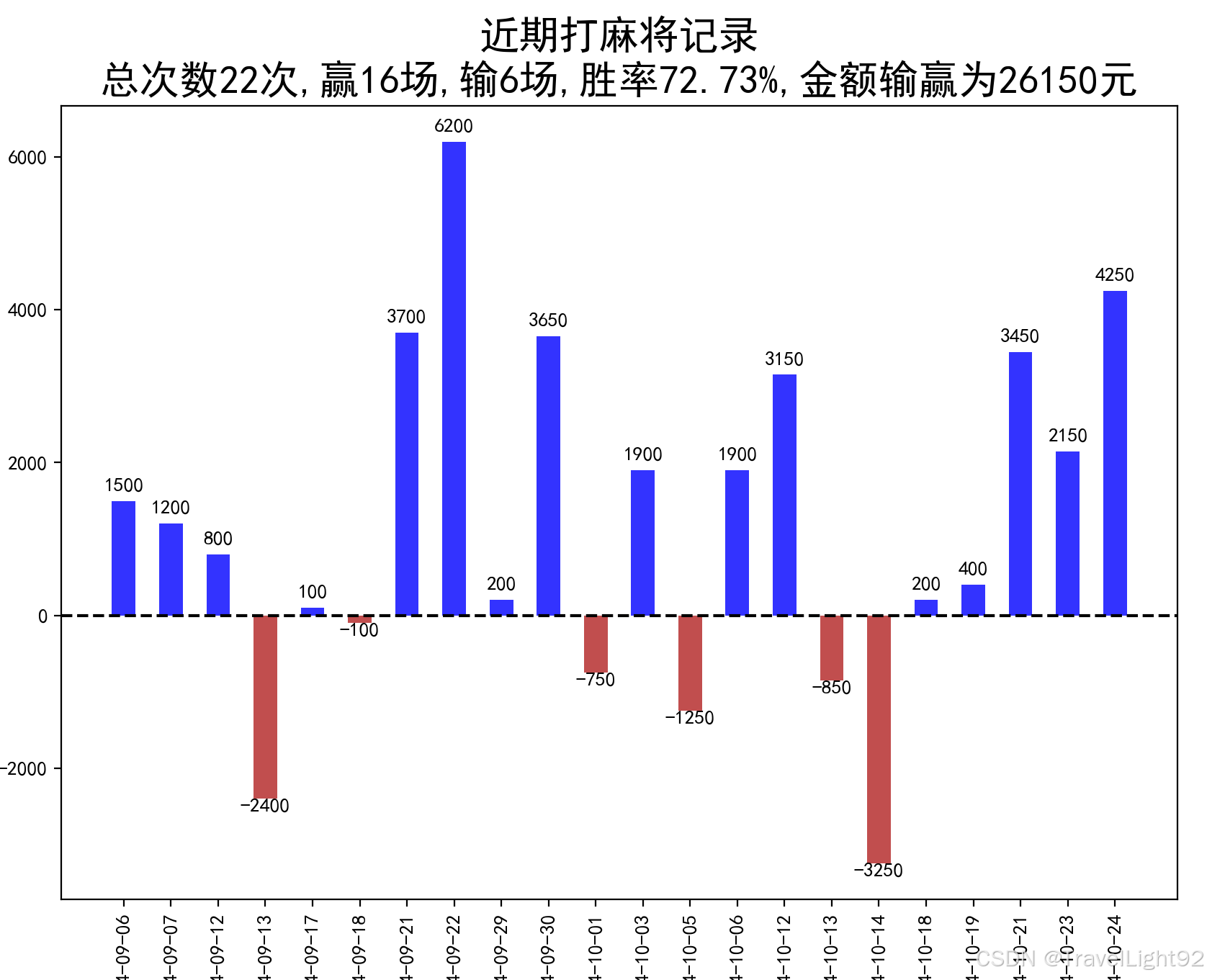
def draw_bar(self):
draw_data = pd.read_excel(io=self.path)
need_data = draw_data[draw_data['play'] == 1][["时间", "play", "输赢", "金额"]]
# 检查数据录入是否有错误
for index in need_data.index:
temp = need_data.loc[index, "输赢"] * need_data.loc[index, "金额"]
if temp < 0:
print('数据录入错误的时间为')
print(need_data.loc[index, "时间"])
raise ValueError("数据录入错误")
my_xlabels = [i.strftime("%Y-%m-%d") for i in need_data["时间"]]
play_numbers = len(need_data)
win_times = len(need_data[need_data["输赢"] == 1])
loose_times = len(need_data[need_data["输赢"] == -1])
win_rate = str(round((win_times / play_numbers) * 100, 2)) + '%'
total_money = round(need_data["金额"].sum())
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 显示负号
plt.figure(figsize=(10, 8))
plt.bar(my_xlabels, need_data['金额'], color=np.where(need_data['金额'] > 0, 'blue', 'firebrick'), alpha=0.8,
width=0.5)
plt.xticks(rotation=90)
plt.axhline(y=0, color='black', linestyle='--')
plt.title("近期打麻将记录\n" + f"总次数{play_numbers}次,赢{win_times}场,输{loose_times}场,胜率{win_rate},金额输赢为{total_money}元",
fontsize=20)
# 数据标注
for a, b in zip(my_xlabels, need_data['金额']):
plt.text(a, np.where(b > 0, b + 100, b - 200), '%d' % b, ha='center', va='bottom', fontsize=10)
plt.show()
def get_result(self):
self.calculate_info()
if self.use_z:
self.try_z()
if self.use_t:
self.try_t()
if self.if_draw:
self.draw_bar()
if __name__ == '__main__':
# make_data = [1 if i %7==1 else 0 for i in range(365)]
# dm = DaMajiang(use_z=True,if_draw=False,raw_data=make_data)
dm = DaMajiang(use_z=True)
dm.get_result()
# 输出内容
不犯取伪错误的情况下,样本量至少要 62 个
目前采集的样本数 51
----运用Z检验进行验证----
----开始验证近期打牌概率,与之前是否相同----
z-test: -2.0932827432500782 p-value: 0.036323922190464236
原本假设周六周日打牌,根据近期观察的情况判断,在假设历史打牌概率为0.29的情况下
经过观察记录近期打牌的次数,这一系列事件的发生概率为 0.0363
结论----拒绝原假设,近期数据的均值与假设历史数据的均值不同----
打牌概率下限: 0.32
打牌概率上限: 0.54
近期打牌均值为: 0.43137254901960786
--------------------------------------------------
----运用T检验进行验证----
验证近期数据是否与往期数据发生改变
t-test: -2.0932827432500782 p-value: 0.03693189558919915
原本假设周六周日打牌,根据近期观察的情况判断,在假设历史打牌概率为0.29的情况下
经过观察记录近期打牌的次数,这一系列事件的发生概率为 0.0369
结论----拒绝原假设,近期数据的均值与假设历史数据的均值不同----
T检验打牌概率下限: 0.32
T检验打牌概率上限: 0.54
近期打牌均值为: 0.43137254901960786


 浙公网安备 33010602011771号
浙公网安备 33010602011771号