《线性代数》5. 线性系统与矩阵的逆

什么是线性系统

系统这个概念有点抽象，之前学的矩阵就可以看作是一个系统，线性系统和初中学的线性方程组是比较类似的。比如：

\(\begin{cases}x + 2y = 5\\3x+4y = 6\end{cases}\)

但这里的重点是线性，所谓线性就是，未知数只能是一次方项。像 \(x^{2} - 1 = 0\)、\(\sqrt{z} - 4 = 0\) 以及 \(sin(x) = π\) 就是非线性方程组，因为它们的未知数不是一次方项。

所谓线性系统就是若干个线性方程组织在了一起，我们研究线性系统的一个最重要的原因就是我们要解这个线性方程组。可能有人觉得解线性方程组还不简单，虽然这只是个计算问题，但随着学习的深入，会发现这是非常有意义的。我们不仅可以把生活中的问题建模成线性系统（比如经济、电路、化学，都可以建模成线性系统），而且通过解决线性系统，我们还能解决线性代数内部的一些问题。

关于如何解析线性方程组，我们目前最先想到的应该就是消元法，比如有 \(n\) 个未知数，先消去一个，会剩下 \(n - 1\) 个未知数。不断重复这一过程，最终只剩下 \(1\) 个未知数，然后求值。求完值之后，将该值带入，继续求下一个未知数。我们举个例子来感受一下：

\(\begin{cases}x + 2y + 4z = 7\\3x + 7y + 2z = -11\\2x + 3y + 3z = 1\end{cases}\)

将第一个方程左右两边乘以 6、第二个方程左右两边乘以 2、第三个方程左右两边乘以 3。

\(\begin{cases}6x + 12y + 24z = 42\\6x + 14y + 4z = -22\\6x + 9y + 9z = 3\end{cases}\)

方程一减去方程二，方程一减去方程三，可得出：

\(\begin{cases}-2y + 20z = 64\\3y + 15z = 39\end{cases}\)

此时我们就消去了一个未知数，然后重复这一过程，继续消下一个。将方程一乘以 3，方程二乘以 2。

\(\begin{cases}-6y + 60z = 192\\6y + 30z = 78\end{cases}\)

将两个式子相加，可得 \(90z = 270\)，解得 \(z = 3\)。将 \(z\) 带入可得 \(y = -2\)，将 \(y\) 和 \(z\) 带入可得 \(x = -1\)。

以上就是消元法，在这个过程中我们涉及了两个操作：

• 一个方程的左右两边同时乘以一个常数。
• 一个方程加（减）另一个方程。
• 当然两个方程还可以交换位置。

高斯消元法

上面在解方程的时候，并没有涉及到矩阵，但我们也可以直接基于矩阵来解决这个线性系统问题。

\(\begin{cases}x + 2y + 4z = 7\\3x + 7y + 2z = -11\\2x + 3y + 3z = 1\end{cases}\)

首先这个方程组，我们可以拆分成一个矩阵和两个列向量。

\(\begin{Bmatrix}1 & 2 & 4\\3 & 7 & 2\\2 & 3 & 3\end{Bmatrix} · \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}7\\-11\\1\end{pmatrix}\)

或者更进一步，我们还可以将未知数给扔掉（因为未知数只是一个名字而已），并将结果合并到系数矩阵中，合并之后的结果我们称为增广矩阵。

\(\begin{Bmatrix}1 & 2 & 4 & 7\\3 & 7 & 2 & -11\\2 & 3 & 3& 1\end{Bmatrix}\)

很明显，增广矩阵的每一行代表了方程组中的每一个方程，之前在方程组中的所有操作，都可以在矩阵中完成。比如方程一、二、三分别乘上 6、2、3：

\(\begin{Bmatrix}6 & 12 & 24 & 42\\6 & 14 & 4 & -22\\6 & 9 & 9 & 3\end{Bmatrix}\)

第二行、第三行分别减去第一行：

\(\begin{Bmatrix}6 & 12 & 24 & 42\\0 & 2 & -20 & -64\\0 & -3 & -15 & -39\end{Bmatrix}\)

第一行再除以 6，话说之前第一行没有必要乘以 6 的，不过为了清晰，我们乘上去，然后再除回来。

\(\begin{Bmatrix}1 & 2 & 4 & 7\\0 & 2 & -20 & -64\\0 & -3 & -15 & -39\end{Bmatrix}\)

让第一行减去第二行：

\(\begin{Bmatrix}1 & 0 & 24 & 71\\0 & 2 & -20 & -64\\0 & -3 & -15 & -39\end{Bmatrix}\)

让第二行乘以 3，第三行乘以 2：

\(\begin{Bmatrix}1 & 0 & 24 & 71\\0 & 6 & -60 & -192\\0 & -6 & -30 & -78\end{Bmatrix}\)

让第三行加上第二行：

\(\begin{Bmatrix}1 & 0 & 24 & 71\\0 & 6 & -60 & -192\\0 & 0 & -90 & -270\end{Bmatrix}\)

让第三行除以 -90：

\(\begin{Bmatrix}1 & 0 & 24 & 71\\0 & 6 & -60 & -192\\0 & 0 & 1 & 3\end{Bmatrix}\)

让第二行加上 "第三行乘以 60"

\(\begin{Bmatrix}1 & 0 & 24 & 71\\0 & 6 & 0 & -12\\0 & 0 & 1 & 3\end{Bmatrix}\)

让第二行再除以 2：

\(\begin{Bmatrix}1 & 0 & 24 & 71\\0 & 1 & 0 & -2\\0 & 0 & 1 & 3\end{Bmatrix}\)

让第一行减去 "第三行乘以 24"：

\(\begin{Bmatrix}1 & 0 & 0 & -1\\0 & 1 & 0 & -2\\0 & 0 & 1 & 3\end{Bmatrix}\)

以上就是我们得到的最终结果，三个未知数的值分别是 -1、-2、3，并且在方程组中的操作对应到矩阵中就是：

• 矩阵的某一行可以乘以一个常数
• 矩阵的某一行可以加减另一行，比如第二行加减第一行。当然加减之前也可以先乘积，比如第二行乘以 \(m\) 的结果和第一行乘以 \(n\) 的结果相加减，也是可以的，因为矩阵的某一行可以乘以任意的常数。所以我们上面的推导过程是有些啰嗦的，因为很多步骤完全可以合成一步，不过学习的过程中展示的详细一些也是好的。
• 矩阵的两行可以任意交换位置。

以上就是高斯消元法，可以自己没事从网上找几道题测试一下，不过对于程序员来说，我们有 Numpy。

import numpy as np

x = np.array(
    [
        [1, 2, 4],  # x + 2y + 4z
        [3, 7, 2],  # 3x + 7y + 2z
        [2, 3, 3],  # 2x + 3y + 3z
    ]
)
result = np.array([7, -11, 1])

print(np.linalg.solve(x, result))  # [-1. -2.  3.]

很简单，直接就计算出来了。但需要注意：Numpy 解出来的结果是浮点数，比如未知数 \(x\) 的值为 \(\frac{\sqrt{3}}{2}\)，那么 Numpy 给出来的结果就是 0.86602···。在程序开发中这没有问题，因为结果本来就是浮点数，但如果你要是作为一名学生准备交作业就尴尬了，你必须猜出来 0.86602··· 怎么来的。因为你直接写 0.86602···，那么老师一看就知道你这是机器算的。

线性方程组解的结构

我们上面的方程组都是有唯一解的，也就是 \(n\) 个未知数，\(n\) 个方程。但很多线性系统可能有无数解，或者压根没有解，那么这些情况要怎么处理呢？我们举个例子：

\(\begin{cases} x + y + 2z = 3\\-x + 3y - 5z = 7\\2x - 2y + 7z = 1\end{cases}\)，对应的增广矩阵是：\(\begin{Bmatrix}1 & 1 & 2 &3\\-1 & 3 & -5 & 7\\2 & -2 & 7 & 1\end{Bmatrix}\)

我们让第二行加上第一行，第三行减去"第一行乘以 2"：

\(\begin{Bmatrix}1 & 1 & 2 &3\\0 & 4 & -3 & 10\\0 & -4 & 3 & -5\end{Bmatrix}\)

先把第二行和第三行的第一个元素变为 0，然后再把第三行的第二个元素变为 0，然后第三个未知数就解出来了。再将第二行的第三个未知数变为 0，这样第二个未知数就解出来了，最后再调整第一行求出第一个未知数。如果未知数超过 3 个，也是同样的道理。

目前第二行和第三行的第一个元素已经变成 0 了，接下来我们把第三行的第二个元素变成 0，只需要让第三行加上第二行即可。

\(\begin{Bmatrix}1 & 1 & 2 &3\\0 & 4 & -3 & 10\\0 & 0 & 0 & 5\end{Bmatrix}\)

但是尴尬的一幕出现了，此时第三行的第三个元素也变成 0 了，这就意味着 \(0·x + 0·y + 0·z = 5\)，显然这是不可能的，因此意味着该方程没有解。

再来看个例子：\(\begin{cases} -x + 2y + 3z = 0\\x - 4y - 13z = 0\\-3x + 5y + 4z = 0\end{cases}\)，对应的增广矩阵是：\(\begin{Bmatrix}-1 & 2 & 3 &0\\1 & -4 & -13 & 0\\-3 & 5 & 4 & 0\end{Bmatrix}\)

第一行乘上 -1，第二行加上第一行，第三行加上第一行乘以 -3：

\(\begin{Bmatrix}1 & -2 & -3 &0\\0 & -2 & -10 & 0\\0 & -1 & -5 & 0\end{Bmatrix}\)

第三行乘以 -2 再加上第二行：

\(\begin{Bmatrix}1 & -2 & -3 &0\\0 & -2 & -10 & 0\\0 & 0 & 0 & 0\end{Bmatrix}\)

因为最后一项是永远满足的，所以此时相当于三个未知数，但只有两个方程。相信你已经知道结果了，我们继续往下推。我们让第一行减去第二行，第二行除以 -2：

\(\begin{Bmatrix}1 & 0 & 7 &0\\0 & 1 & 5 & 0\\0 & 0 & 0 & 0\end{Bmatrix}\)

结果为：\(x = -7z, y = -5z\)，显然这个方程是有无数解的。\(z\) 取任意一个值，都能得到一组 \(x, y,z\)，满足方程组。

我们用 Numpy 来算一下，看看会有什么结果。

import numpy as np

x = np.array(
    [
        [1, 1, 2],
        [-1, 3, -5],
        [2, -2, 7],
    ]
)
result = np.array([3, 7, 1])
# 该方程无解
try:
    print(np.linalg.solve(x, result))
except np.linalg.LinAlgError as e:
    print(e)  # Singular matrix
# 我们看到报错了，报错的结果是奇异矩阵

x = np.array(
    [
        [-1, 2, 3],
        [1, -4, -13],
        [-3, 5, 4],
    ]
)
result = np.array([0, 0, 0])
# 该方程有无数组解，会从满足条件的解中给出一个，显然 -0、-0、-0 是满足的
print(np.linalg.solve(x, result))  # [-0. -0. -0.]

总结一下：

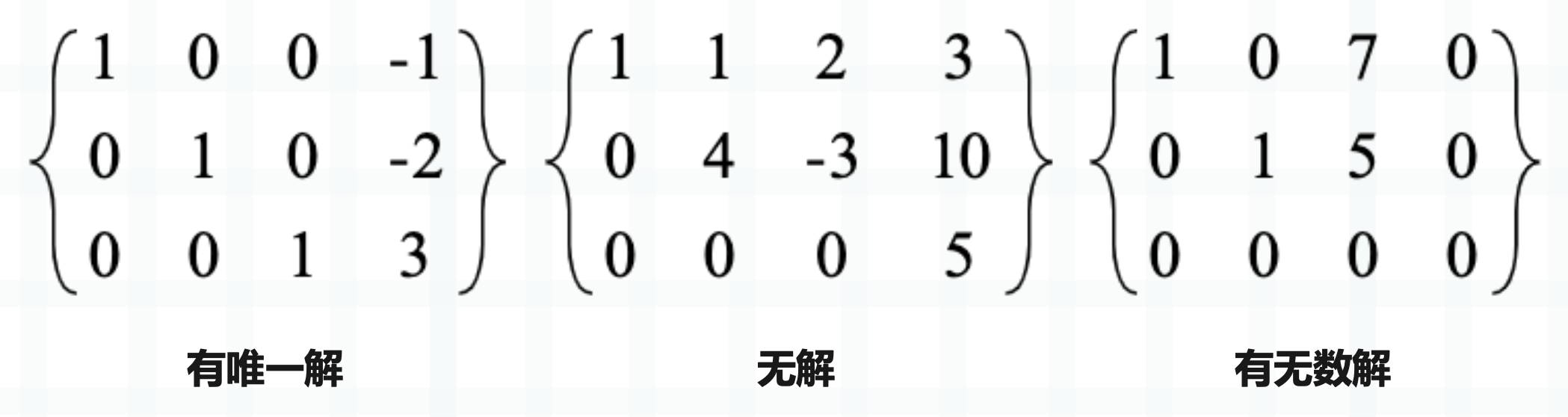
这是我们上面的几个矩阵化简之后的结果，从形式上来看，相信很容易得出哪些矩阵是有解，哪些是无解的。

这里我们给出一个结论：

1）方程个数小于未知数个数，那么方程无解或有无数解。

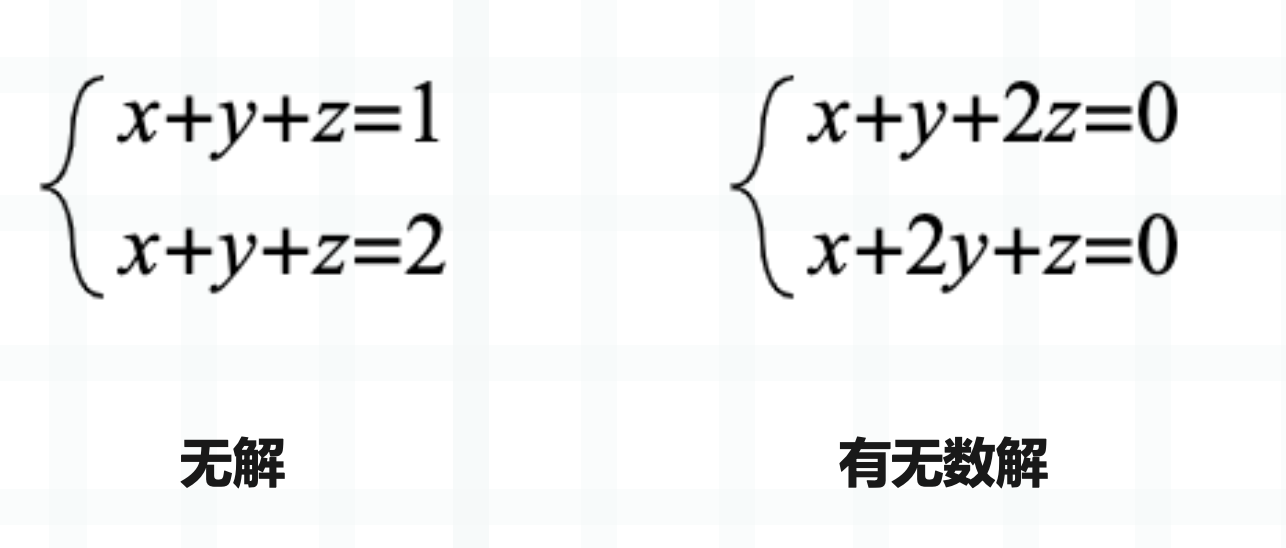
2）方程个数等于未知数个数，那么方程无解或有无数解或有唯一解。

3）方程个数大于未知数个数，那么方程无解或有无数解或有唯一解。

最后再来补充一下齐次线性方程组，等号右边都是 0 的线性方程组就是齐次线性方程组。从性质上来说，齐次线性方程组和线性方程组是一样的，但齐次线性方程组最大的特点是它至少有一个解，这个解就是零解。

线性系统与矩阵的逆

之前我们介绍了矩阵的逆，但是却没有说如何去求，那么下面就来看看更多和矩阵的逆有关的的东西。先来回顾一下，如果 \(AB = BA = I\)，则称 \(B\) 是 \(A\) 逆矩阵，记作：\(B = A^{-1}\)，显然只有方阵才有逆矩阵。

那么假设矩阵 \(A\) 有逆矩阵，那么如何求解呢？比如矩阵 \(A\) 如下：

\(A = \begin{Bmatrix}1 & 2\\3 & 4\end{Bmatrix}\)

显然 \(A\) 的逆矩阵和 \(A\) 具有相同的形状，假设 \(A^{-1} = \begin{Bmatrix}x_{11} & x_{12}\\x_{21} & x_{22}\end{Bmatrix}\)，那么有 \(\begin{Bmatrix}1 & 2\\3 & 4\end{Bmatrix} · \begin{Bmatrix}x_{11} & x_{12}\\x_{21} & x_{22}\end{Bmatrix} = \begin{Bmatrix}1 & 0\\0 & 1\end{Bmatrix}\)。而矩阵和矩阵相乘，可以拆分成矩阵和多个向量相乘，然后再相加。

\(\begin{Bmatrix}1 & 2\\3 & 4\end{Bmatrix} · \begin{pmatrix}x_{11}\\x_{21}\end{pmatrix} = \begin{pmatrix}1\\0\end{pmatrix}\)

\(\begin{Bmatrix}1 & 2\\3 & 4\end{Bmatrix} · \begin{pmatrix}x_{12}\\x_{22}\end{pmatrix} = \begin{pmatrix}0\\1\end{pmatrix}\)

当然我们也可以直接计算，没有必要拆开，只是我们知道可以这么做即可。

\(\begin{cases}x_{11} + 2·x_{21} = 1\\3·x_{11} + 4·x_{21} = 0\\x_{12} + 2·x_{22} = 0\\3·x_{12} + 4·x_{22}=1\end{cases}\)

四个未知数，四个方程，所以求矩阵的逆本质上是一个求解线性系统的问题。而且上面虽然是 4 个方程，但我们可以拆成两个线性系统，每个线性系统有两个方程。

\(\begin{Bmatrix}1 & 2 & 1\\3 & 4 & 0\end{Bmatrix}\)

\(\begin{Bmatrix}1 & 2 & 0\\3 & 4 & 1\end{Bmatrix}\)

然后我们使用高斯消元求解：

\(\begin{Bmatrix}1 & 2 & 1\\3 & 4 & 0\end{Bmatrix} = \begin{Bmatrix}1 & 2 & 1\\0 & -2 & -3\end{Bmatrix} = \begin{Bmatrix}1 & 2 & 1\\0 & 1 & \frac{3}{2}\end{Bmatrix} = \begin{Bmatrix}1 & 0 & -2\\0 & 1 & \frac{3}{2}\end{Bmatrix}\)

\(\begin{Bmatrix}1 & 2 & 0\\3 & 4 & 1\end{Bmatrix} = \begin{Bmatrix}1 & 2 & 0\\0 & -2 & 1\end{Bmatrix} = \begin{Bmatrix}1 & 2 & 0\\0 & 1 & -\frac{1}{2}\end{Bmatrix} = \begin{Bmatrix}1 & 0 & 1\\0 & 1 & -\frac{1}{2}\end{Bmatrix}\)

最终解得：\(A^{-1} = \begin{Bmatrix}-2 & 1\\\frac{3}{2} & -\frac{1}{2}\end{Bmatrix}\)。

可以看到，我们将求矩阵的逆转换成了一个线性系统问题。

• 如果无解，说明是奇异矩阵（不可逆）；
• 如果有唯一解，说明是非奇异矩阵（可逆）；
• 至于无数解，答案是不可能有无数解。

那么为什么不可能有无数解呢？原因很简单，在高斯消元的时候，只有出现全部为 0 的自由列，方程组才可能出现无数解。但对于乘积是单位矩阵来说，这是不可能出现的。

另外矩阵的逆有一个很重要的计算功能，对于线性系统 \(Ax = b\)，通过矩阵的逆，可以很轻松的求出未知数。

\(Ax = b\)

\(A^{-1}·A·x = A^{-1}·b\)

\(x = A^{-1}·b\)

我们只需要让 \(A\) 的逆和 \(b\) 相乘即可，当然这和直接求解所需的计算量相差不大。但有时候系数矩阵是不变的，如果 \(A\) 不变、\(b\) 会动态变化，那么就会大大加快计算速度，因为 \(A^{-1}\) 只需要计算一次。