[CEOI2014] The Wall【最短路】

洛谷P6545 [CEOI2014] The Wall

Description

在一张 \(n\times m\) 的网格图上有若干关键格子，且格子 \((1,1)\) 必定是关键格子。你需要建造一座城墙使得它包括所有关键格子，具体的，城墙是沿着网格线上的一条连续闭曲线，每经过一段网格线一次，就会产生对应的代价。请你最小化这一代价。

\(n,m\le 400\)，对所有花费 \(v\) 有 \(1\le v\le 10^9\)。

Solutions

首先给出引理：

最终的城墙一定会包含左上角的点到每个关键格子左上角的点的最短路。

证明：考虑一个合法的建造城墙方案，如果它不含某条最短路，那么这条最短路会被城墙分为若干部分，在墙内的与在墙外的交替出现，此时如果将城墙扩展使得在墙外的部分都进入墙中，那么答案一定不劣：

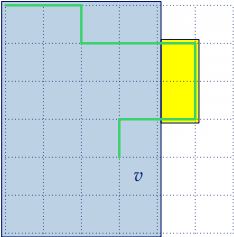
例如图中绿色为一条最短路，\(v\) 为一个关键格子，蓝色为城墙，那么此时将城墙扩张到包含黄色区域，那么根据最短路的定义，新包括进来的这一段绿色城墙作为最短路，一定比原来那部分的城墙花费代价更少。同时，扩张城墙只扩大了区域，不会影响已经包含进去的格子。因此这样扩展城墙答案一定不劣。

于是我们先跑一遍最短路，找到左上角点到每个关键格子左上角点的最短路，那么问题转化为了找一条从 \(1\) 号格子出发的包括所有关键点且不穿过最短路树上的边时的最小权闭合回路。

可以考虑将每个格点拆成 \(4\) 个小点，从左上开始顺时针依次编号为 \((0,1,2,3)\)，它们互相连边权为 \(0\) 的边组成一个 \(4\) 个点的环表示切换方向。如果一个格子必须被包含，那么就强制让组成它的四个端点不被经过，那么由于必须包含最短路，最终闭合回路会到达该格子的左上角点，并在要求不能经过其端点的情况下绕它一圈。

如果一条边在最短路上，被强制要求经过，如果这条边是竖直的，就让上端点的 \((2, 3)\) 边不连，下端点的 \((0,1)\) 不连；如果这条边是水平的，就让左端点的 \((1,2)\) 不连，右端点的 \((0,3)\) 不连。

对于原图上的一条正常边，就让其两端点相对的两个分点对应连比权为该边权值的边即可。最终问题是求从 \((1,1)\) 格子的 \(0\) 号点出发的最小闭合回路，可以改为将 \(0\) 号点删去，求从 \(1\) 号点到 \(3\) 号点的最短路，就相当于求出了最小闭合回路。

最终复杂度 \(\mathcal O(nm\log nm)\)。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=410,M=N*N*4;
int n,m,r[N][N],c[N][N],p[N][N],first[M],cnt,tp,f[M];
struct node{
	int v,nxt;ll w;
}e[M<<2];
inline int id(int tp,int x,int y){return tp*(n+1)*(m+1)+(x-1)*(m+1)+y;} 
inline void add(int u,int v,ll w){e[++cnt].v=v;e[cnt].w=w;e[cnt].nxt=first[u];first[u]=cnt;}
inline void Add(int u,int v,ll w){
//	if(tp) cout<<u<<" "<<v<<" "<<f[u]<<" "<<f[v]<<endl;
	if(tp&&(f[u]||f[v])) return;
	add(u,v,w);add(v,u,w);
}
ll dis[M];bool vis[M];
int tot,last[M];
int pd[N][N][2];
inline ll dijkstra(int s,int t){
	priority_queue<pair<ll,int> > q;
	memset(dis+1,0x3f,sizeof(ll)*(tot));
	memset(vis+1,0,sizeof(bool)*(tot));
	memset(last+1,0,sizeof(int)*(tot));
	dis[s]=0;q.push(make_pair(0,s));
	while(!q.empty()){
		int u=q.top().second;q.pop();
		if(vis[u]) continue;vis[u]=1;
		for(int i=first[u];i;i=e[i].nxt){
			int v=e[i].v;
			if(dis[u]+e[i].w<dis[v]){
				dis[v]=dis[u]+e[i].w;last[v]=u;
				q.push(make_pair(-dis[v],v));
			}
		}
	}
	return dis[t];
}
inline void limit(int u,int v){
	int x1=(u-1)/(m+1)+1,y1=(u-1)%(m+1)+1,x2=(v-1)/(m+1)+1,y2=(v-1)%(m+1)+1;
  	if(x1==x2) pd[x1][min(y1,y2)][0]=1;
	else pd[min(x1,x2)][y1][1]=1;
}
int main(){
	scanf("%d%d",&n,&m);
	f[1]=1;
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j){
			scanf("%d",&p[i][j]);
			if(p[i][j])
				f[id(2,i,j)]=f[id(3,i,j+1)]=f[id(1,i+1,j)]=f[id(0,i+1,j+1)]=1;
		}
	tot=id(3,n+1,m+1);
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m+1;++j)
			scanf("%d",&r[i][j]);
	for(int i=1;i<=n+1;++i)
		for(int j=1;j<=m;++j)
			scanf("%d",&c[i][j]);
	for(int i=1;i<=n+1;++i)
		for(int j=1;j<=m+1;++j){
			if(i<n+1) Add(id(0,i,j),id(0,i+1,j),r[i][j]);
			if(j<m+1) Add(id(0,i,j),id(0,i,j+1),c[i][j]);
		}
	dijkstra(id(0,1,1),id(0,n+1,m+1));
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j)
			if(p[i][j]){
				int now=id(0,i,j);
				while(now!=id(0,1,1)){
					limit(last[now],now);
					now=last[now];
				}
			}
	cnt=0;
	memset(first+1,0,sizeof(int)*(tot));tp=1;
	for(int i=1;i<=n+1;++i)
		for(int j=1;j<=m+1;++j){
			if(!pd[i-1][j][1]) Add(id(0,i,j),id(1,i,j),0);
			if(!pd[i][j][0]) Add(id(1,i,j),id(2,i,j),0);
			if(!pd[i][j][1]) Add(id(2,i,j),id(3,i,j),0);
			if(!pd[i][j-1][0]) Add(id(3,i,j),id(0,i,j),0);
		}
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m+1;++j)
			Add(id(3,i,j),id(0,i+1,j),r[i][j]),Add(id(2,i,j),id(1,i+1,j),r[i][j]);
	for(int i=1;i<=n+1;++i)
		for(int j=1;j<=m;++j)
			Add(id(1,i,j),id(0,i,j+1),c[i][j]),Add(id(2,i,j),id(3,i,j+1),c[i][j]);
	printf("%lld\n",dijkstra(id(1,1,1),id(3,1,1)));
	return 0;
}