【NOI2016】 优秀的拆分【后缀数组】

传送门

容易想到的是枚举 \(AA\) 的末尾位置 \(i\)，那么 \(ans=\sum_{i}f_ig_{i+1}\)。

其中 \(f_i\) 表示以第 \(i\) 位作为结尾的形如 \(AA\) 的串的数量，\(g_i\) 表示以第 \(i\) 位作为开头的形如 \(AA\) 的串的数量。

对于 \(f,g\) 的求解，直接 \(\mathcal O(n^2)\) 枚举加哈希判断就可以拿到 \(95\) 分，但显然，并不在考场上的我们不希望放弃剩下 \(5\) 分，因此接下来我们将介绍一个此类题目的经典套路。

考虑枚举 \(A\) 的长度 \(len\)，然后将原串中第 \(len,2len,3len,\dots\) 位作为关键点。那么所有的 \(AA\) 串都必定恰好经过两个关键点，不妨设其为 \(l,r\)，显然 \(r=l+len\)。

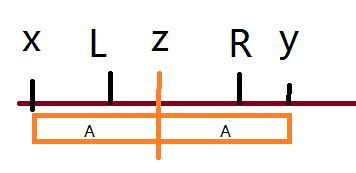
如图所示，\(x\sim L\)段与\(z\sim R\)段相同，\(L+1-Z\)段与\(R+1-y\)段相同。其中前者是 \(pre[L]\) 与 \(pre[R]\) 的公共后缀，后者是 \(suf[L+1]\) 与 \(suf[R+1]\) 的公共前缀。

因此，我们先求出 \(lcs\) 为 \(pre[L]\) 与 \(pre[R]\) 的最长公共后缀，\(lcp\) 为 \(suf[L+1]\) 与 \(suf[R+1]\) 的最长公共前缀。那么只要 \(lcs+lcp>len\)，我们就能找到前后各一段合法 的开始位置与结束位置，差分统计即可。

view code>

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int T,n,f[N],g[N];
char s[N],t[N];
inline void mem(){
	scanf("%s",s+1);n=strlen(s+1);
	for(int i=1;i<=n;++i) t[i]=s[n+1-i];
	memset(f+1,0,sizeof(int)*(n+1));
	memset(g+1,0,sizeof(int)*(n+1));
}

struct SA{
	int height[N],sa[N],c[N],y[N],rk[N],st[N][20];
	char ch[N];
	inline void init(int n){
		memset(rk+1,0,sizeof(int)*(n));
		memset(c+1,0,sizeof(int)*(n));
		memset(y+1,0,sizeof(int)*(n));
	}
	inline void getsa(int n,int m,char *s){
		for(int i=1;i<=m;++i) c[i]=0;
		for(int i=1;i<=n;++i) rk[i]=s[i]-'a'+1,c[rk[i]]++;
		for(int i=2;i<=m;++i) c[i]+=c[i-1];
		for(int i=1;i<=n;++i) sa[c[rk[i]]--]=i;
		for(int k=1;;k<<=1){
			int num=0;
			for(int i=n-k+1;i<=n;++i) y[++num]=i;
			for(int i=1;i<=n;++i) if(sa[i]>k) y[++num]=sa[i]-k;
			for(int i=1;i<=m;++i) c[i]=0;
			for(int i=1;i<=n;++i) c[rk[i]]++;
			for(int i=2;i<=m;++i) c[i]+=c[i-1];
			for(int i=n;i>=1;--i) sa[c[rk[y[i]]]--]=y[i],y[i]=rk[i];
			num=0;
			for(int i=1;i<=n;++i){
				if(i!=1&&y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]) rk[sa[i]]=num;
				else rk[sa[i]]=++num;
			}
			if(num==n) break;
			m=num;
		}
	}
	inline void getheight(int n,char *s){
		int k=0;
		for(int i=1;i<=n;++i){
			if(rk[i]==1){k=0;height[1]=0;continue;}
			if(k>0) k--;
			int x=i,y=sa[rk[i]-1];
			while(x+k<=n&&y+k<=n&&s[x+k]==s[y+k]) ++k;
			height[rk[i]]=k;
		}
		for(int i=1;i<=n;++i) st[i][0]=height[i];
		for(int i=1;i<17;++i)
			for(int j=1;j+(1<<i)-1<=n;++j) st[j][i]=min(st[j][i-1],st[j+(1<<i-1)][i-1]);
	}
	inline int lcp(int x,int y){
		x=rk[x];y=rk[y];
		if(x>y) swap(x,y);
		++x;
		int len=log2(y-x+1);
		return min(st[x][len],st[y-(1<<len)+1][len]);
	}
}A,B;

inline void solve(){
	A.init(n+1);B.init(n+1);
	A.getsa(n,26,s);A.getheight(n,s);
	B.getsa(n,26,t);B.getheight(n,t);
	for(int len=1;(len<<1)<=n;++len){
		int tot=n/len;
		for(int i=1;i<tot;++i){
			int lcp=min(len-1,B.lcp(n-i*len+2,n-(i+1)*len+2));
			int lcs=min(len,A.lcp(i*len,(i+1)*len));
			if(lcs+lcp<len) continue;
			int tmp=lcs+lcp-len+1;
			f[i*len-lcp]++;f[i*len+tmp-lcp]--;
			g[(i+1)*len+lcs-tmp]++;g[(i+1)*len+lcs]--;
		}
	}
	for(int i=1;i<=n;++i) f[i]+=f[i-1],g[i]+=g[i-1];
	long long ans=0;
	for(int i=1;i<n;++i)
		ans+=1ll*g[i]*f[i+1];
	printf("%lld\n",ans);
}
int main(){
	scanf("%d",&T);
	while(T--){
		mem();
		solve();
	}
	return 0;
}