算法第三章上机实践报告

算法第三章上机实践报告

实践报告

问题描述

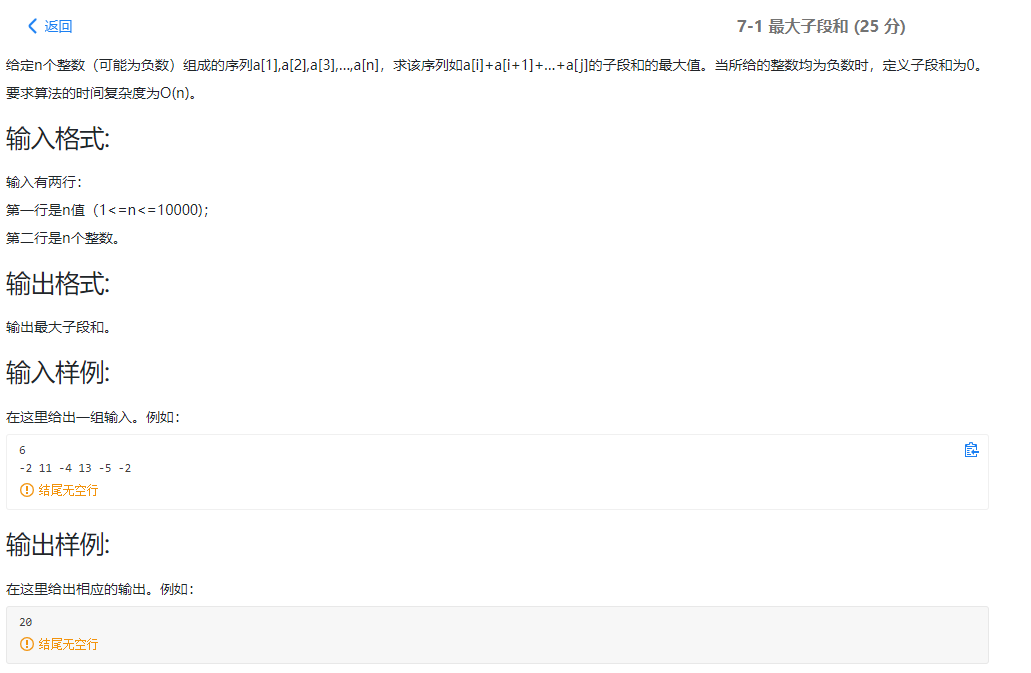
算法描述

用数组num存储输入数据，m数组存储最大子段和，其中m[i] (1≤ i ≤n) 表示以i位置为开头的序列的字段和的最大值。

设置max记录m数组中的最大值，negative记录输入数据负数的个数，初始化为0，若negative==n，则直接输出0。否则，初始化m数组的n号元素和max为num数组的n号元素，执行for循环，由n-1循环至1，当m[k+1]>0时，m[k] = num[k] + m[k+1]，否则，m[k] = num[k]，然后判断m[k]是否大于max，若大于，则max=m[k]，最后输出max。

问题求解

根据最优子结构性质，列出递归方程式

当k等于n时，m[k] = num[n]

当m[k+1]>0时，m[k] = num[k] + m[k+1]

当m[k+1]≤0时，m[k] = num[k]

给出填表法中表的维度、填表范围和填表顺序

表的维度：一维

填表范围：1 ~ n-1

填表顺序：从右往左

代码

#include <iostream>
using namespace std;

int num[10001];
int m[10001];

int maxsum(int n){
	int max=m[n];
	for(int k=n-1;k>0;k--){
		if(m[k+1]>0)
			m[k] = num[k] + m[k+1];
		else
			m[k] = num[k];
		if(m[k]>max)
			max = m[k];
	}
	return max;
}

int main(){
	int n,negative=0;
	cin >> n;
	for(int i=1;i<=n;i++){
		cin >> num[i];
		if(num[i]<0)
			negative++; 
	}
	if(negative==n){
		cout << 0;
		return 0;
	}
	m[n]=num[n];
	cout << maxsum(n);
	return 0;
} 

分析该算法的时间和空间复杂度

• 时间复杂度：算法为与n相关的for循环，时间复杂度为O(n)

• 空间复杂度：用了大小为n的数组存储由对应下标开始的最大子段和，所以空间复杂度为O(n)

心得体会（对本次实践收获及疑惑进行总结）

• 边界条件是最小子问题的最优解，多为初始化条件，不一定是递推结束的条件
• 边界条件（初始化条件）常为数组开头或结尾元素，要根据题目分析
• 最重要的是找到子问题和状态转移方程

对动态规划算法的理解和体会

动态规划问题的特点

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

（2）重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。

解题的一般思路

1. 划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

2. 确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。状态的选择要满足无后效性。

3. 确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策， 状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

4. 寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。