回溯法之批处理作业调度

回溯法之批处理作业调度

---

1. 问题描述

​ n个作业集合{1, 2, ..., n}。每个作业先由机器1处理，再由机器2处理。作业i需要机器j处理的时间为M_ij 。

Mij	机器1	机器2
作业1	2	1
作业2	3	1
作业3	2	3

​ 对于一个确定的作业调度，设F_ij 是作业i在机器j上完成的具体时间。所有作业在机器2上完成的具体时间(时刻)之和f称为该作业调度的完成时间和。
​ 要求：对于给定的n个作业，制定最佳作业调度方案(一个排列)，使其完成时间和达到最小

2. 问题分析

​ 3个作业的6种可能的调度方案是1-2-3；1-3-2；2-1-3；2-3-1；3-1-2；3-2-1；它们所相应的完成时间和分别是19,18，20,21,19,19。易见，最佳调度方案是1-3-2，其完成时间和为18。
​ F_i1、F_i2表示事件i分别在机器1和机器2上完成的时间。

作业顺序	Fi1	Fi2	f
begin	0	0	0
①	2	3	3
③	4	7	10
②	7	8	18

​ 假设此时1-2-3的作业调度已经完成计算，遍历到了1-3-2的序列。
​ 首先是①，将调用f1 += M[x[j]][1];表示作业1在机器1需要2时间才能完成，接下来使用f2[i] = ((f2[i - 1] > f1) ? f2[i - 1] : f1) + M[x[j]][2];比较F₀₂ 和 F₁₁ 的大小，即需要等待前一个作业在机器2完成计算才能在机器2开始本次作业，再使用F₀₂ 和 F₁₁的较大值F₁₁+作业2在机器2的工作时间1得到F₁₂为3，在使用f += f2[i]，将3赋值给f。
​ 到③，调用f1 += M[x[j]][1];，F₂₁变为2+2=4，再比较F₁₂和F₂₁，将较大的F₂₁+3=7赋值给F₂₂。f变为10。
​ 到②，F₃₁变为7，比较F₂₂和F₃₁，将7+1=8复制给F₃₂，最终将f变为18，得到最终结果。

3. 代码求解

​ 该问题的解空间：排列树：
​
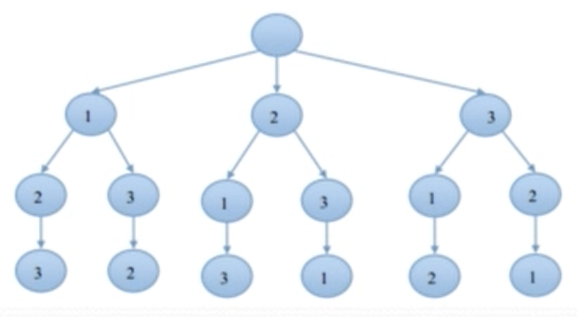
​ 使用到的全局变量：

M        各作业所需的处理时间
x        当前作业调度
bestx    当前最优作业调度
f2       机器2完成的处理时间
f1       机器1完成的处理时间
f        完成时间和
bestf    当前最优值
n        作业数

​ 核心求解代码：

void BackTrack(int i) {
    // i > n表示已经访问到叶子结点，即一个作业调度遍历完成
    // 将此时的最优解暂时保存到bestx中
    if (i > n) {
        for (int j = 1; j <= n; j++) {
            bestx[j] = x[j];
            bestf = f;
        }
    } else {
        // 若没找到此时的最优解，则对当前的求解树的子节点遍历求解
        for (int j = i; j <= n; j++) {
            // 上述的问题求解过程
            f1 += M[x[j]][1];
            f2[i] = ((f2[i - 1] > f1) ? f2[i - 1] : f1) + M[x[j]][2];
            f += f2[i];
            // 如果f小于当前的最小值，代表这个分支可以继续运算，否则直接裁去该分支，达到优化算法的目的
            if (f < bestf) {
                swap(i, j);
                // 递归求解
                BackTrack(i + 1);
                // 递归运算后，需要回退到上一层排列树
                swap(i, j);
            }
            // 本条路径求解结束后回退到原本的状态
            f1 -= M[x[j]][1];
            f -= f2[i];
        }
    }
}

4. 完整代码

/**
 * 回溯法求解批处理作业调度问题
 * 
 * 主要由BackTrack函数递归调用求解问题
 * 使用bsetf保存最优解，bestx保存最优的作业调度序列
 **/
#include <stdio.h>
#include <stdlib.h>

#define MAXROW 4
#define MAXCOL 3

/**
 * M        各作业所需的处理时间
 * x        当前作业调度
 * bestx    当前最优作业调度
 * f2       机器2完成的处理时间
 * f1       机器1完成的处理时间
 * f        完成时间和
 * bestf    当前最优值
 * n        作业数
 **/
int M[MAXROW][MAXCOL], x[MAXROW], bestx[MAXROW], f2[MAXROW], f1, f, bestf, n;

// 值交换函数
void swap(int i, int j) {
    int tmp = x[i];
    x[i] = x[j];
    x[j] = tmp;
}

void BackTrack(int i) {
    // i > n表示已经访问到叶子结点，即一个作业调度遍历完成
    // 将此时的最优解暂时保存到bestx中
    if (i > n) {
        for (int j = 1; j <= n; j++) {
            bestx[j] = x[j];
            bestf = f;
        }
    } else {
        // 若没找到此时的最优解，则对当前的求解树的子节点遍历求解
        for (int j = i; j <= n; j++) {
            f1 += M[x[j]][1];
            f2[i] = ((f2[i - 1] > f1) ? f2[i - 1] : f1) + M[x[j]][2];
            f += f2[i];
            if (f < bestf) {
                swap(i, j);
                BackTrack(i + 1);
                swap(i, j);
            }
            f1 -= M[x[j]][1];
            f -= f2[i];
        }
    }
}

void main() {
    n = 3;
    bestf = INT_MAX;
    M[1][1] = 2;M[1][2] = 1;
    M[2][1] = 3;M[2][2] = 1;
    M[3][1] = 2;M[3][2] = 3;

    for (int i = 0; i <= n; i++) {
        f2[i] = 0;
        x[i] = i;
    }

    BackTrack(1);
    printf("%d\n", bestf);
    for (int i = 1; i <= n; i++) {
        printf("%d ", bestx[i]);
        if (i != n)
            printf("-> ");
    }
    printf("\n");

    system("pause");
}