TypeDB Forces 2023 (Div. 1 + Div. 2, Rated, Prizes!) D E

D. Game on Axis

tag： 思维 图论

题目链接

题意：

给你一个n个点的图，每个点i都有一个值a[i]，走到点 i 之后就会接着走到点 i+a[i]
若 i+a[i] 不在 1到n 的范围内，则停止走动
初始时你位于点1，你可以任意修改a[i] = y，修改范围 −n≤y≤n
现在问你有多少种修改方法，使得你最终能够停下

做法：

这题妙就妙在一个反向建图
我们对所有的点进行反向建边，同时将点0和所有能够停下的点进行连边
再从点0开始dfs，依次访问这颗树的各个节点
只要点在这颗树中，那么显然这个点能够一路走到0，它是能走完的点，而那些不在树中的点就属于停不下来那种
分类一下点1在树中和不在树中的情况

• 停的下来
  算不合法情况，对于包括1之后通过的所有节点，他们不能连自己的后继（即子树中成员），和那些停不下来的点。
• 停不下来
  算合法情况，对于包括1之后通过的所有节点，他们可以连树上的任意一个点，注意到0的方法有n+1种

代码：

#define fst std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout << std::fixed << std::setprecision(20)
#define le "\n"
#define ll long long 
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+50;
const int mod=998244353;
int a[N],sz[N],fa[N];
vector<int> g[N];

void solve(){
    ll n; cin>>n;
    for(int i=0;i<=n;i++) sz[i] = 0, g[i].clear();

    int x,nxt;
    for(int i=1;i<=n;i++){
        cin>>x;
        nxt = i+x;
        if(nxt>n||nxt<1) nxt = 0;
        g[nxt].push_back(i); //只存指向nxt的边，能指到0就说明可以走完
        a[i] = nxt; 
    }
    function<void(int)> dfs = [&](int u){
        sz[u] = 1;
        for(auto v: g[u]){
            dfs(v);
            sz[u] += sz[v];
        }
    };
    dfs(0);
    
    if(sz[1]){
        ll ans = n*(2*n+1);
        int u = 1;
        while(u){
            ans -= sz[u]+(n-(sz[0]-1)); //连后面的点是违法的，连到环里也是违法的
            u = a[u];
        }
        cout<<ans<<le;
    }
    else{
        vector<bool> vis(n+1);
        int u = 1;
        ll ans = 0;
        while(!vis[u]){
            vis[u] = 1;
            ans += sz[0]-1+n+1;//连到走的完的树里是合法的,走到不存在的点是合法的
            u = a[u];
        }
        cout<<ans<<le;
    }
}

int main() {
    int t; cin>>t;
    while(t--){
        solve();
    }            
    return 0;
}  

E. The Harmonization of XOR

tag：构造

题目链接

题意：

给你 n,k,x 三个数
你需要使用 1~n 每个数一次，构造k个段，使得每段的异或和为x

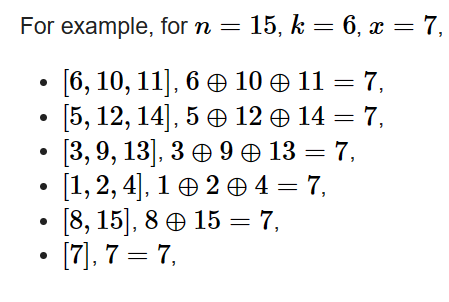
如果构造不出来输出 NO, 否咋输出 YES 和构造

做法：

从构造结果反推，我们有k段 异或和为x 的段
将所有段异或起来得到sum1,k为偶数时 sum1 = 0, k为奇数时 sum1 = x
sum1应等于 1~n 的异或和， 若不等则显然无法构造
接下来的构造只需寻找二元组[x,y]即可
构造k-1对，剩下的所有数再组成一队，因为sum已经确定，所以剩下那队也一定合法。

代码：

#define fst std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout << std::fixed << std::setprecision(20)
#define le "\n"
#define ll long long 
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+50;
const int mod=998244353;

void solve(){
    int n,k,x; cin>>n>>k>>x;
    int sum = 0;
    for(int i=1;i<=n;i++) sum^=i;
    int tmp = (k%2==0? 0 : x); //sum = x^x^...^x 连续k个x的异或
    if(sum!=tmp){
        cout<<"NO"<<le;
        return;
    }
    vector<vector<int>> ans;
    vector<int> vis(n+1);
    vector<int> res;
    for(int i=1;i<=n;i++){
        if(vis[i]) continue;
        else{
            if((i^x)>i &&(i^x)<=n && ans.size()!=k-1){
                ans.push_back({i,i^x});
                vis[i] = vis[i^x] = 1;
            }
            else{
                res.push_back(i);
                vis[i] = 1;
            }
        }
    }
    if(ans.size()!=k-1) cout<<"NO"<<le;
    else{
        cout<<"YES"<<le;
        for(auto i: ans){
            cout<<2<<" "; 
            for(auto j: i){
                cout<<j<<" ";
            }
            cout<<le;
        }
        cout<<res.size()<<" ";
        for(auto i: res) cout<<i<<" ";
        cout<<le;
    }
}

int main() {
    int t; cin>>t;
    while(t--){
        solve();
    }   
    return 0;
}