G. New Year and Original Order（cf908G）

G. New Year and Original Order（cf908G）

tag：数位dp

题目链接

题意：

有函数S(x),将x中的每一位数升序排序，排序得到的数即为数的贡献。
如S(1) = 1, S(5) = 5, S(50394) = 3459, S(353535) = 333555。
我们需要求 ：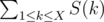

做法：

首先一眼数位dp，我们需要思考的是如何设计一个状态能将数抽象成需要的状态
先思考每一个数的贡献如何计算，下面用114514举例

// 114514 -> 111445
// 111000 + 440 + 5
// 既然大于等于1的数有6个 那么我把后面的贡献算到前面去
// 则1的贡献变成111111 4的贡献变成330 5的贡献变成4
// 大于等于2的数有3个 虽然2原本没贡献，但我们和上面一样做一遍
// 2的贡献变为111 4的贡献变为220 5的贡献变为3
// 3的贡献变为111 4的贡献变为110 5的贡献变为2
// 4的贡献变为111 5的贡献变为1
// 111111 + 111 + 111 + 111 + 1 + 0 + 0 + 0 + 0 + 0 = 111445

因此我们只需要枚举1~9，而数字'i'的贡献即为 11...1 (原数有几个大于等于i的数就有几个1）,累加就是答案了。
同时我们也知道 114514 和 111445 都是等价的，所以可以设计 dp[1005][1005][10][2]计入方案数 //前i位有j个大于等于数字k的方案 01表示是否受到限制
这题求方案数啥的都是很传统的方法，难想到的还是上面的贡献计算
数位dp复建，分别写了直接推和记忆化搜索两版

代码：

#define fst std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout << std::fixed << std::setprecision(20)
#define le "\n"
#define ll long long 
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+50;
const int mod=1e9+7;
void add(ll &x, ll y){
    x += y;
    if(x>=mod) x-=mod;
}
ll dp[1005][1005][10][2]; //前i位有j个大于等于数字k的方案 01表示是否受到限制

int main() {
    string s; cin>>s;
    int n = s.size();
    s = " "+s;
    for(int i=1;i<=9;i++) dp[0][0][i][1] = 1;
    
    for(int i=1;i<=n;i++){
        for(int j=0;j<=n;j++){
            for(int k=0;k<10;k++){
                for(int limit=0;limit<=1;limit++){
                    for(int p=0;p<=(limit ? (s[i]-'0'):9);p++){
                        add(dp[i][j+(k<=p)][k][limit&&p==s[i]-'0'],dp[i-1][j][k][limit]);
                    }
                }
            }
        }
    }    
    
    ll ans = 0;
    for(int k=1;k<=9;k++){
        ll base = 1;
        for(int j=1;j<=n;j++){
            add(ans,(base*dp[n][j][k][0])%mod);
            add(ans,(base*dp[n][j][k][1])%mod);
            base = (base*10+1)%mod;
        }
    }
    cout<<ans<<le;
    return 0;
}

#define fst std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout << std::fixed << std::setprecision(20)
#define le "\n"
#define ll long long 
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+50;
const int mod=1e9+7;
void add(ll &x, ll y){
    x += y;
    if(x>=mod) x-=mod;
}
int A[N];
ll w[N],dp[1005][1005][10][2]; 

ll dfs(int pos,int cnt,int num,bool limit){
    if(!pos) return w[cnt];
    if(dp[pos][cnt][num][limit]!=-1) return dp[pos][cnt][num][limit];
    ll ans = 0;
    for(int i=0;i<=(limit ? A[pos]: 9);i++){
        add(ans,dfs(pos-1,cnt+(i>=num),num,limit&&i==A[pos])); 
    }
    dp[pos][cnt][num][limit] = ans;
    return ans;
}

void f(string s){
    memset(A,0,sizeof(A));
    memset(dp,-1,sizeof(dp));
    int n = 0;
    reverse(s.begin(),s.end());
    for(auto c: s) A[++n] = c-'0';

    w[1] = 1;
    for(int i=2;i<=n;i++) w[i]=(w[i-1]*10+1)%mod;

    ll res = 0;
    for(int i=1;i<=9;i++){
        add(res,dfs(n,0,i,1));
    }
    cout<<res<<le;
}

int main() {
    string s; cin>>s;
    f(s);
    return 0;
}