Loading

机器学习实战——支持向量机：软间隔分类、多项式内核、相似特征

目录

支持向量机（Support Vector Machine，SVM）是一个功能强大并且全面的机器学习模型，它能够执行线性或非线性分类、回归，以及异常值检测任务。SVM特别适用于中小型复杂数据集的分类。

线性SVM分类

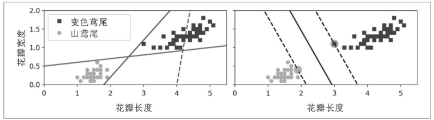
image
左图显示了三条可能得线性分类器的决策边界。其中虚线非常不匹配，剩下两条实线有些过拟合，
右图的实线代表SVM分类器的决策边界，这条线分离了两个类，而且尽可能远离了最近的训练实例（也就是虚线部分）

SVM对特征的缩放非常敏感.
image

软间隔分类

传统的硬间隔分类有两个问题：

  1. 只有数据线性可分离才有效
  2. 对异常值非常敏感
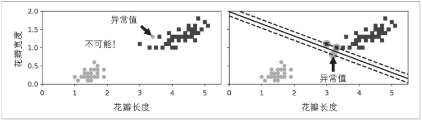
    image
    图中可以看出硬间隔分类对异常值特别敏感。
    要避免硬间隔带来的问题，就需要用软间隔分类，这样就能视目标尽可能保持在两侧。
    使用Scikit-Learn创建SVM模型时，我们可以指定许多超参数。C是这些超参数之一。
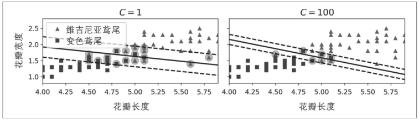
    image
  • 左图中C设置为较低的值
  • 右图中C设置为较高的值
    右图的间隔冲突很多，所以如果你的SVM模型过拟合，可以尝试降低C来进行正则化。

以下Scikit-Learn代码可加载鸢尾花数据集，缩放特征，然后训练线性SVM模型（使用C=1的LinearSVC类和稍后描述的hinge损失函数）来检测维吉尼亚鸢尾花：

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # 花瓣长度，花瓣宽度
y = (iris["target"] == 2).astype(np.float64)  # 判断是否是 Iris virginica

svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("linear_svc", LinearSVC(C=1, loss="hinge")),
    ])

svm_clf.fit(X, y)

svm_clf = Pipeline([("scaler", StandardScaler()), ("linear_svc", LinearSVC(C=1, loss="hinge"))])：这行代码创建了一个Pipeline，它包含了两个步骤：特征缩放和线性SVM分类。

  • scaler", StandardScaler()：这一步是特征缩放，使用StandardScaler来标准化特征，即将特征值减去均值后除以标准差，使得每个特征的平均值为0，标准差为1。这是SVM等基于距离的算法常见的预处理步骤。
  • linear_svc", LinearSVC(C=1, loss="hinge")：这一步是线性SVM分类。LinearSVC是scikit-learn中实现线性SVM的类。C=1是正则化强度的倒数，用于控制正则化的强度，防止过拟合。loss="hinge"指定了损失函数为hinge loss，这是SVM常用的损失函数。

预测的结果如下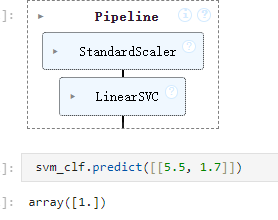：image
花瓣长度是5.5 宽度是1.7的是Virginica花（因为array是1）

非线性SVM分类

有很多数据集远不是线性可分离的。处理非线性数据集的方法之一是添加更多特征，比如多项式特征。
为了使用Scikit-Learn来实现这个想法，创建一个包含PolynomialFeatures转换器）的Pipeline，然后是StandardScaler和LinearSVC。
在卫星数据集上进行测试：一个用于二元分类的小数据集，数据点的形状是两个交织的半圆。
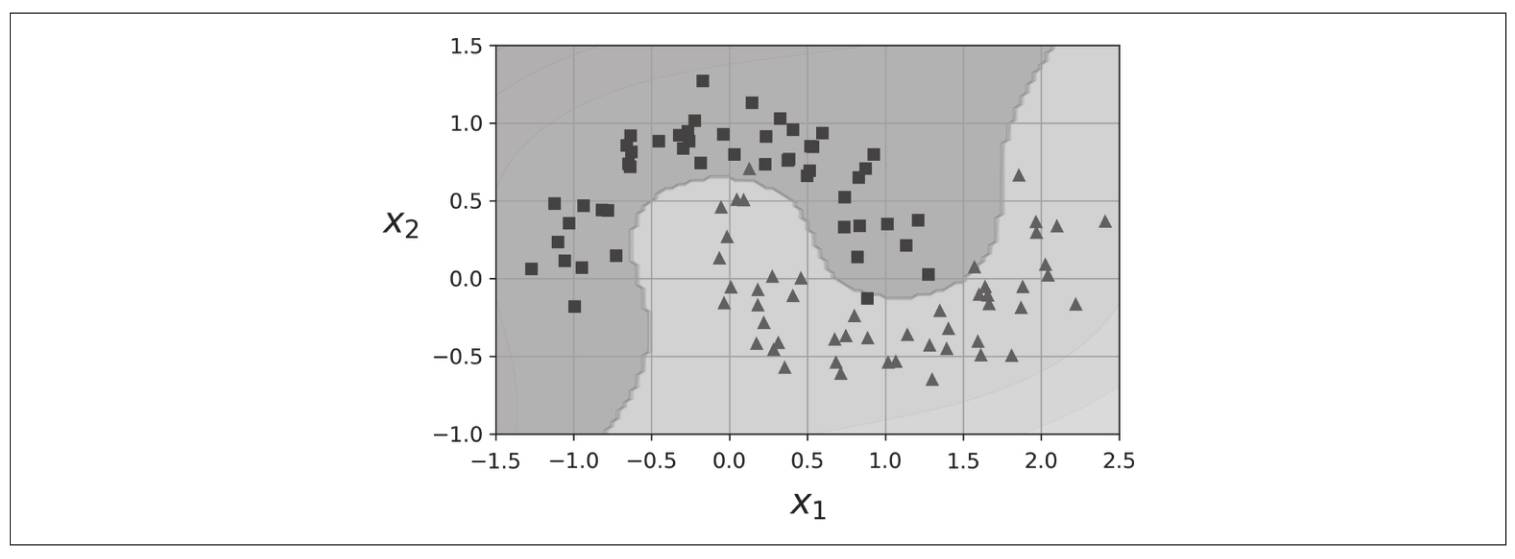
image
使用多项式特征分类的线性SVM分类器：

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

X, y = make_moons(n_samples=100, noise=0.15)
polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge"))
    ])
polynomial_svm_clf.fit(X, y)

  • from sklearn.datasets import make_moons：从sklearn.datasets模块导入make_moons函数，该函数用于生成二维的、非线性的、可分离的数据集，通常用于测试分类算法在非线性决策边界上的性能。

  • X, y = make_moons(n_samples=100, noise=0.15)：使用make_moons函数生成一个包含100个样本的数据集，并添加一定的噪声（噪声参数为0.15）。X是包含样本特征的二维数组，y是包含样本标签的一维数组。

  • 创建一个Pipeline，其中包含三个步骤：多项式特征生成PolynomialFeatures、特征缩放StandardScaler、以及线性支持向量机分类器LinearSVC

    • 多项式特征生成：PolynomialFeatures(degree=3)将生成原始特征的所有多项式组合，直到3次幂。这有助于将非线性问题转换为线性问题，因为支持向量机（SVM）本质上是线性分类器。
    • 特征缩放：StandardScaler()用于对多项式特征进行标准化处理，使得每个特征的平均值为0，标准差为1。这是必要的，因为多项式特征可能会导致特征值的范围非常大，从而影响SVM的性能。
    • 线性支持向量机分类器：LinearSVC(C=10, loss="hinge")是一个线性支持向量机分类器，其中C=10是正则化强度的倒数（一个较大的C值表示更强的正则化），loss="hinge"指定了使用hinge loss作为损失函数。

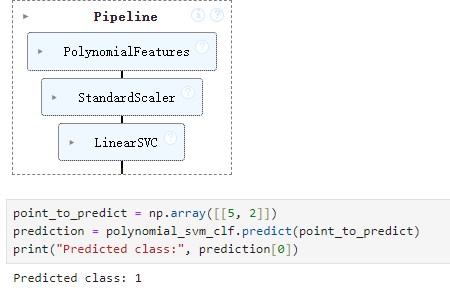
预测结果：image
此时输入5，2,得到的分类是1

多项式内核

如果多项式太低阶，则处理不了非常复杂的数据集。而高阶则会创造出大量的特征，导致模型变得太慢。
但SVM有一个核技巧，产生的结果就跟添加了许多多项式特征一样，但实际上并不需要真的添加。
代码如下：

from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ])
poly_kernel_svm_clf.fit(X, y)

解释：

  • 导入必要的类和函数

    • from sklearn.svm import SVC：从sklearn.svm模块导入SVC类，这是实现支持向量机算法的类。
    • from sklearn.preprocessing import StandardScaler（尽管在您的代码片段中没有直接导入，但根据上下文，我假设您已经做了这一步或者是在其他地方已经导入了StandardScaler）。
    • from sklearn.pipeline import Pipeline（同样，没有直接导入，但根据上下文假设已导入）。

  • Pipeline中的步骤

    • ("scaler", StandardScaler())：第一个步骤是StandardScaler，用于对输入特征进行标准化处理，即减去均值并除以标准差，使得每个特征的平均值为0，标准差为1。这是重要的预处理步骤，因为SVM对特征的尺度非常敏感。
    • ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))：第二个步骤是SVC分类器，配置为使用多项式核 kernel="poly"。多项式核允许SVM在原始特征的非线性组合上工作，从而可能更好地拟合非线性数据。
      • degree=3：指定多项式的度数为3，即考虑原始特征的所有多项式组合，直到3次幂。
      • coef0=1：多项式核中的独立项（也称为偏移量或截距）的系数。在多项式核中，特征映射可能包括常数项、线性项、二次项等，coef0用于调整常数项的权重。
      • C=5：正则化参数C的倒数，用于控制正则化的强度。较小的C值指定了更强的正则化，可能导致模型在训练集上表现更差，但可能具有更好的泛化能力。

结果如图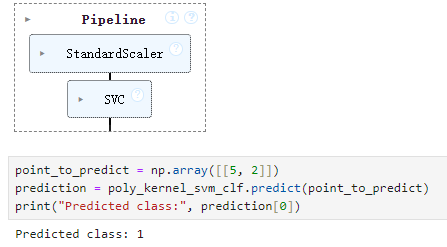：image

相似特征

解决非线性问题的另一种技术是添加相似特征，这些特征经过相似函数计算得出，相似函数可以测量每个实例与一个特定地标之间的相似度。
采用高斯RBF公式作为相似函数：
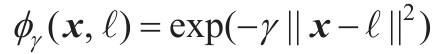
image

  • X：输入样本
  • ℓ：核函数中心点
  • \(\gamma\)：是核函数的一个超参数，控制了高斯核函数的宽度
  • \(||X-ℓ||\)：表示欧几里得距离

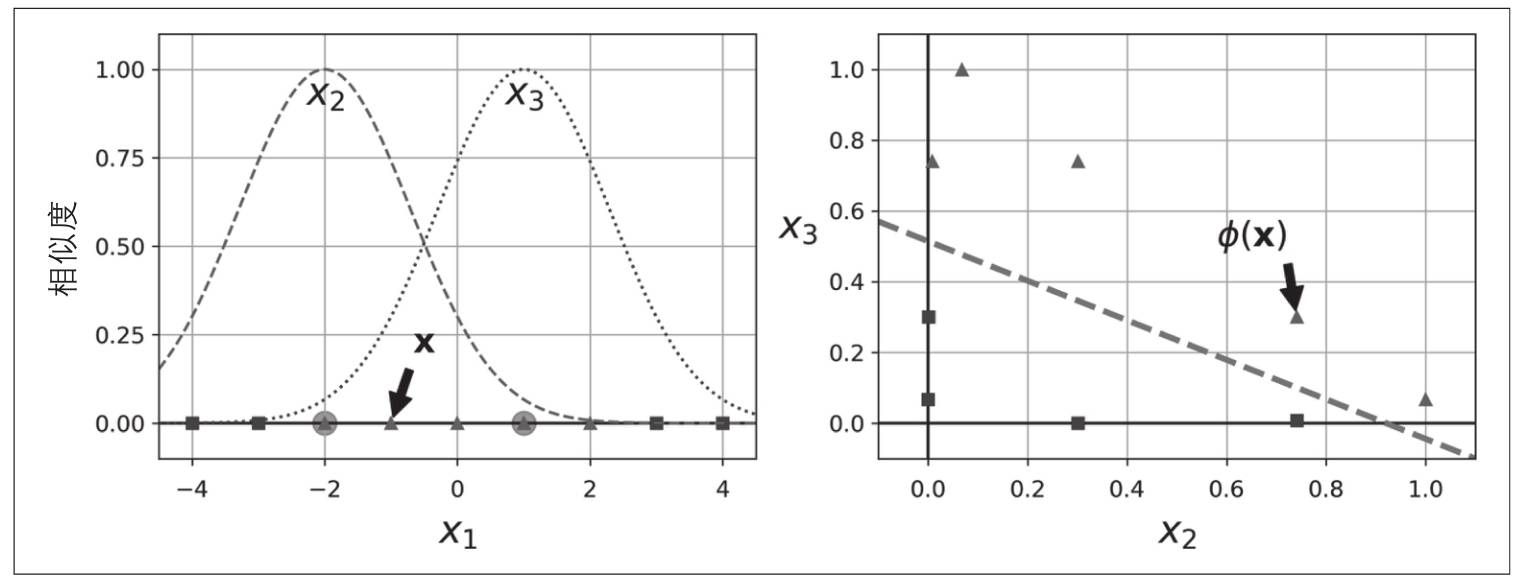
image
如图：
在左图的X1=-2和X1=1添加两个地标，然后用RBF作为相似函数，\(\gamma\)=0.3计算实例X1=-1：

  • -1与第一个地标X1=-2的距离为1
  • -1于第二个地标X2=1的距离为2
    因此新特征为：
  • x2=eps（-0.3×12）≈0.74，
  • x3=eps（-0.3×22）≈0.30
    如上图右边所示，此时数据完成线性分离。

高斯RBF内核

与多项式特征方法一样，相似特征法也可以用任意机器学习算法，但算出所有的附加特征计算代价很昂贵。
使用SVM的核技巧可以达到这样的效果：

rbf_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
    ])
rbf_kernel_svm_clf.fit(X, y)

Pipeline中的步骤：

  • ("scaler", StandardScaler())：这是Pipeline的第一个步骤，用于对输入特征进行标准化处理。标准化是数据预处理中常见的一步，它有助于改善许多机器学习算法的性能，特别是那些对特征尺度敏感的算法，如SVM。
  • ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))：这是Pipeline的第二个步骤，它配置了一个SVC分类器，该分类器使用RBF核。
    • kernel="rbf"：指定使用RBF核。RBF核是一种非线性核，它允许SVM在原始特征的高维空间中学习复杂的决策边界。
    • gamma=5：gamma参数定义了单个训练样本的影响达到最大的距离，或者说是“到达率”的倒数。gamma值越大，单个样本的影响范围越小，这可能导致决策边界更加复杂，但也可能导致过拟合。在RBF核中，gamma是一个重要的超参数，需要根据具体的数据集进行调整。
    • C=0.001：正则化参数C的倒数，用于控制正则化的强度。较小的C值指定了更强的正则化，这可能导致模型在训练集上的表现更差，但有助于防止过拟合，提高模型的泛化能力。

结果：image

使用不同C和\(\gamma\)分类的模型效果不同，增加\(\gamma\)值会使钟形曲线变得更窄，每个实例的影响范围变小，决策边界不规则；
减小\(\gamma\)使钟形曲线变得更宽，每个实例的影响增大，决策边界变得平坦。

模型过拟合就降低\(\gamma\)值，欠拟合就增加\(\gamma\)值

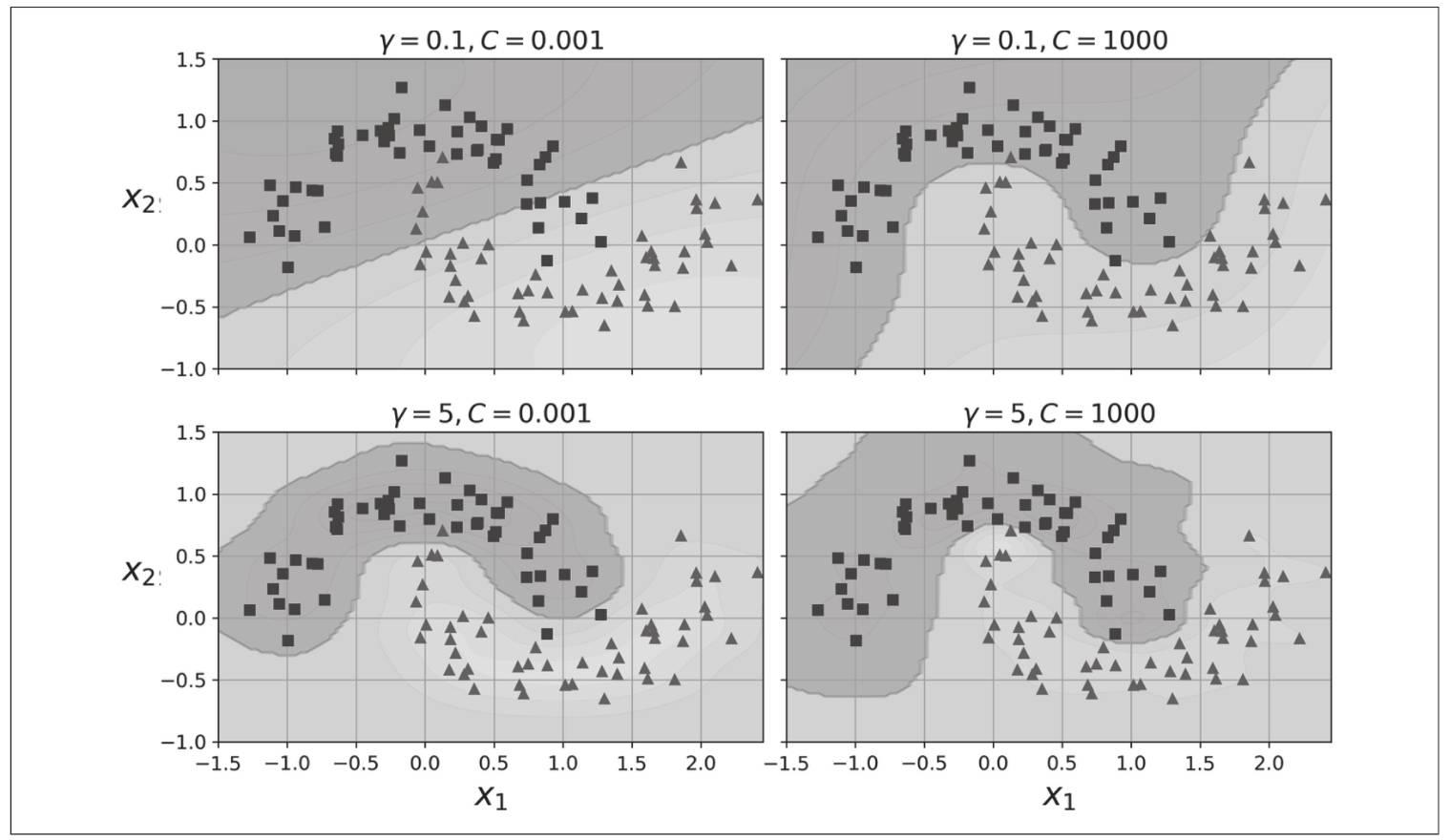
image
如上图针对不同C和\(\gamma\)的SVM分类器

核函数选择

永远先从线性核函数开始尝试（要记住，LinearSVC比SVC（kernel="linear"）快得多），特别是训练集非常大或特征非常多的时候。如果训练集不太大，你可以试试高斯RBF核，大多数情况下它都非常好用。如果你还有多余的时间和计算能力，可以使用交叉验证和网格搜索来尝试一些其他的核函数，特别是那些专门针对你的数据集数据结构的核函数。
image

  • LinearSVC：线性支持向量机
  • SGDClassifier：随机梯度下降
  • SVC：支持向量机（分类）

SVM回归

SVM回归：让尽可能多的实例位于街道上，同事限制不在街道上的实例。街道的宽度由$ \varepsilon$控制。
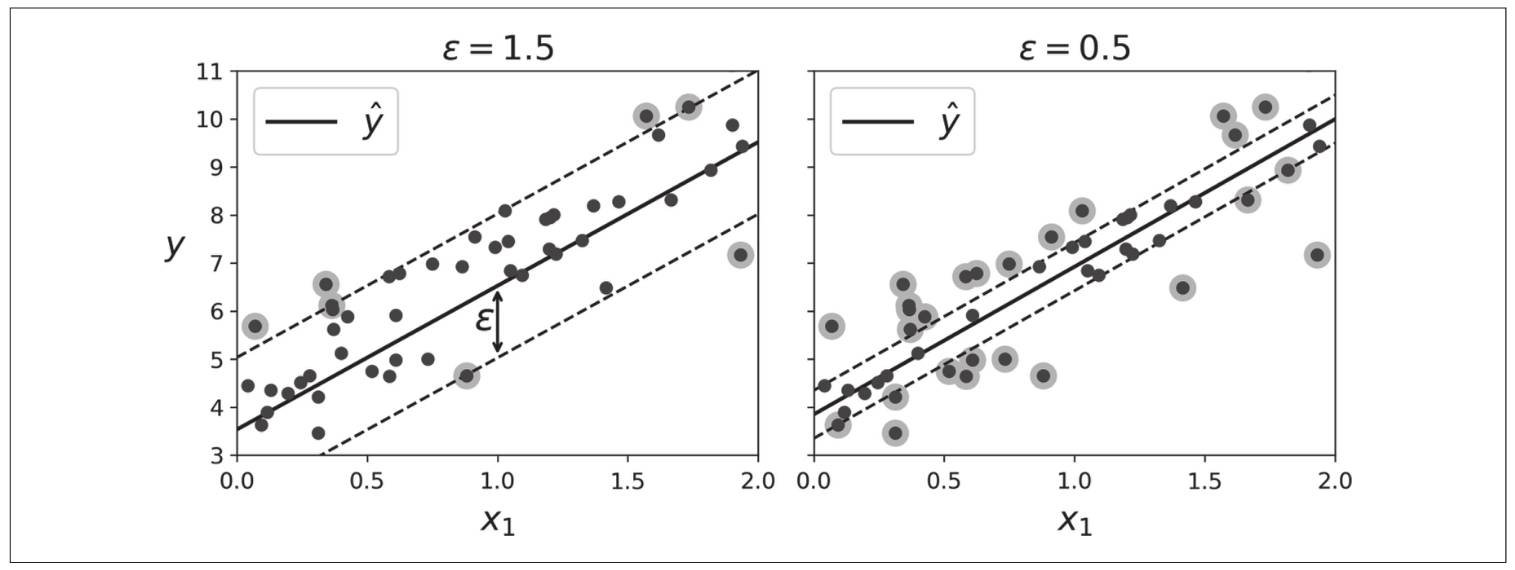
image
左图 \(\varepsilon\)=1.5，右图 \(\varepsilon\)=0.5

在间隔内添加更多的实例不会影响模型的预测。

使用Scikit-Learn的Linear-SVR类来执行线性SVM回归：

from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)

使用Scikit-Learn的SVR类（支持核技巧）:

from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)

模型如下图的左边：
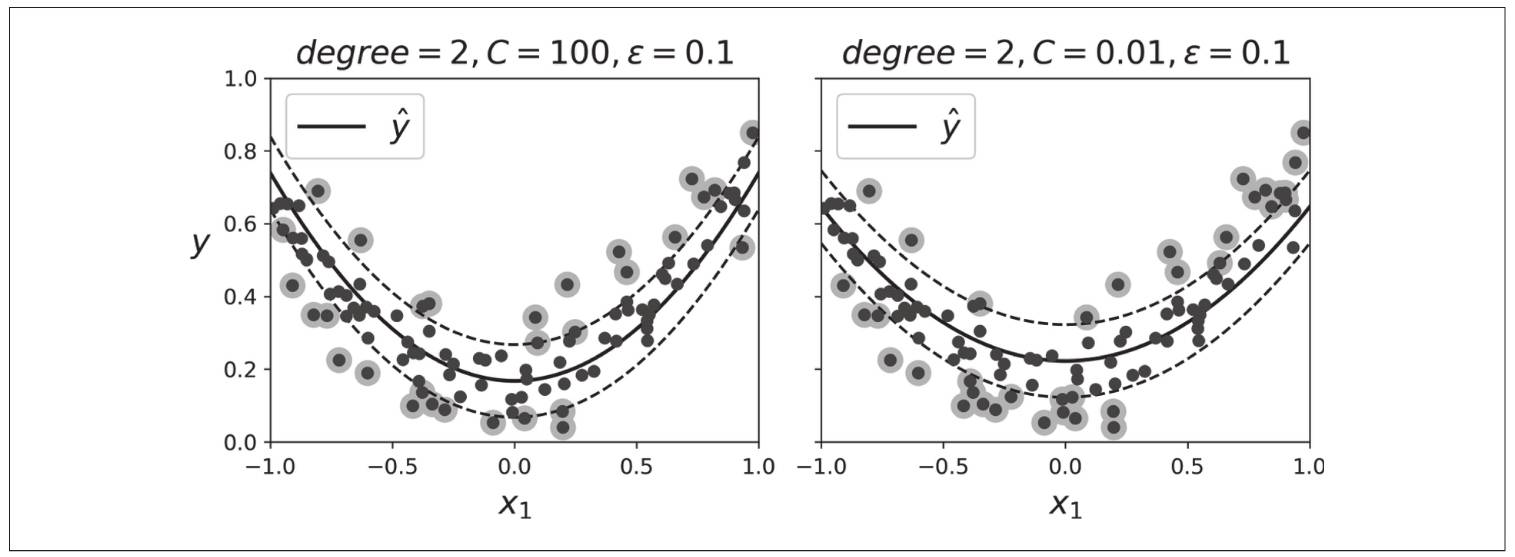
image

左图C很大几乎没有正则化，右图C很小过度正则化

SVR类是SVC类的回归等价物，LinearSVR类也是LinearSVC类的回归等价物。LinearSVR与训练集的大小线性相关（与LinearSVC一样），而SVR则在训练集变大时，变得很慢（SVC也一样）。

5.4工作原理部分跳过

题目

  1. 支持向量机的基本思想是什么？
  2. 什么是支持向量？
  3. 使用SVM时，对输入值进行缩放为什么重要？
  4. SVM分类器在对实例进行分类时，会输出信心分数吗？概率呢？
  5. 如果训练集有成百万个实例和几百个特征，你应该使用SVM原始问题还是对偶问题来训练模型？
  6. 假设你用RBF核训练了一个SVM分类器，看起来似乎对训练集欠拟合，你应该提升还是降低γ（gamma）？C呢？
  7. 如果使用现成二次规划求解器，你应该如何设置QP参数（H、f、A和b）来解决软间隔线性SVM分类器问题？
  8. 在一个线性可分离数据集上训练LinearSVC。然后在同一数据集上训练SVC和SGDClassifier。看看你是否可以用它们产生大致相同的模型。
  9. 在MNIST数据集上训练SVM分类器。由于SVM分类器是个二元分类器，所以你需要使用一对多来为10个数字进行分类。你可能还需要使用小型验证集来调整超参数以加快进度。最后看看达到的准确率是多少？
  10. 在加州住房数据集上训练一个SVM回归模型。

答案：

  1. 支持向量机的基本思想是拟合类别之间可能的、最宽的“街道”。换言之，它的目的是使决策边界之间的间隔最大化，该决策边界分隔两个类别和训练实例。SVM执行软间隔分类时，实际上是在完美分隔两个类和拥有尽可能最宽的街道之间寻找折中方法（也就是允许少数实例最终还是落在街道上）。还有一个关键点是在训练非线性数据集时，记得使用核函数。
  2. 支持向量机的训练完成后，位于“街道”（参考上一个答案）之上的实例被称为支持向量，这也包括处于边界上的实例。决策边界完全由支持向量决定。非支持向量的实例（也就是街道之外的实例）完全没有任何影响。你可以选择删除它们然后添加更多的实例，或者将它们移开，只要一直在街道之外，它们就不会对决策边界产生任何影响。计算预测结果只会涉及支持向量，而不涉及整个训练集。
  3. 支持向量机拟合类别之间可能的、最宽的“街道”（参考第1题答案），所以如果训练集不经缩放，SVM将趋于忽略值较小的特征
  4. 支持向量机分类器能够输出测试实例与决策边界之间的距离，你可以将其用作信心分数。但是这个分数不能直接转化成类别概率的估算。如果创建SVM时，在Scikit-Learn中设置probability=True，那么训练完成后，算法将使用逻辑回归对SVM分数进行校准（对训练数据额外进行5-折交叉验证的训练），从而得到概率值。这会给SVM添加predict_proba（）和predict_log_proba（）两种方法。5.这个问题仅适用于线性支持向量机，因为核SVM只能使用对偶问题。对于SVM问题来说，原始形式的计算复杂度与训练实例m的数量成正比，而其对偶形式的计算复杂度与某个介于m2和m3之间的数量成正比。所以如果实例的数量以百万计，一定要使用原始问题，因为对偶问题会非常慢。
  5. 这个问题仅适用于线性支持向量机，因为核SVM只能使用对偶问题。对于SVM问题来说，原始形式的计算复杂度与训练实例m的数量成正比，而其对偶形式的计算复杂度与某个介于m2和m3之间的数量成正比。所以如果实例的数量以百万计，一定要使用原始问题，因为对偶问题会非常慢。
  6. 如果一个使用RBF核训练的支持向量机对欠拟合训练集，可能是由于过度正则化导致的。你需要提升gamma或C（或同时提升二者）来降低正则化。
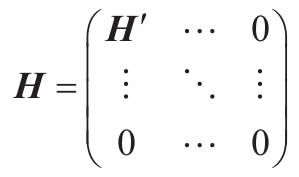
  7. 我们把硬间隔问题的QP参数定义为H'、f'、A'及b'（见5.4.3节）。软间隔问题的QP参数还包括m个额外参数（np=n+1+m）及m个额外约束（nc=2m）。它们可以这样定义：H等于在H'右侧和底部分别加上m列和m行个0：image
    f等于有m个附加元素的f'，全部等于超参数C的值。b等于有m个附加元素的b'，全部等于0。A等于在A'的右侧添加一个m×m的单位矩阵Im，在这个单位矩阵的正下方再添加单位矩阵-Im，剩余部分为0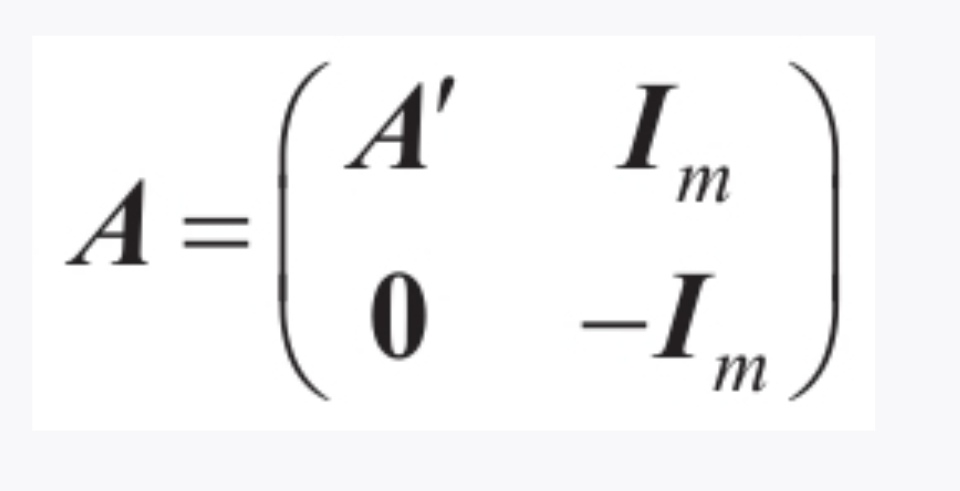：image

对于练习8～10的解答，请参见Jupyter notebooks：https://github.com/ageron/handsonml2的Jupyter notbook。

（我只是大致学一下，内容有不对的也有不详细的，希望多多包涵一下，未来学成归来会重新写一篇文章的！）

posted @ 2024-08-01 16:54  江侠  阅读(122)  评论(0)    收藏  举报