Deep learning:四十五(maxout简单理解)
maxout出现在ICML2013上,作者Goodfellow将maxout和dropout结合后,号称在MNIST, CIFAR-10, CIFAR-100, SVHN这4个数据上都取得了start-of-art的识别率。
从论文中可以看出,maxout其实一种激发函数形式。通常情况下,如果激发函数采用sigmoid函数的话,在前向传播过程中,隐含层节点的输出表达式为:
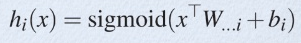
其中W一般是2维的,这里表示取出的是第i列,下标i前的省略号表示对应第i列中的所有行。但如果是maxout激发函数,则其隐含层节点的输出表达式为:
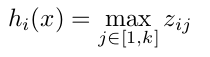
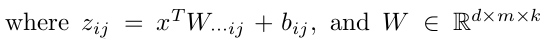
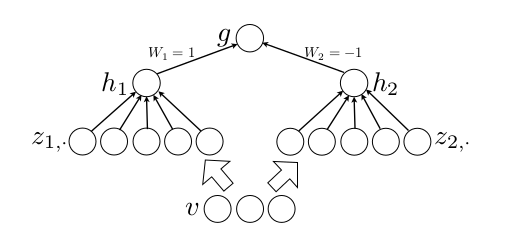
这里的W是3维的,尺寸为d*m*k,其中d表示输入层节点的个数,m表示隐含层节点的个数,k表示每个隐含层节点对应了k个”隐隐含层”节点,这k个”隐隐含层”节点都是线性输出的,而maxout的每个节点就是取这k个”隐隐含层”节点输出值中最大的那个值。因为激发函数中有了max操作,所以整个maxout网络也是一种非线性的变换。因此当我们看到常规结构的神经网络时,如果它使用了maxout激发,则我们头脑中应该自动将这个”隐隐含层”节点加入。参考一个日文的maxout ppt 中的一页ppt如下:
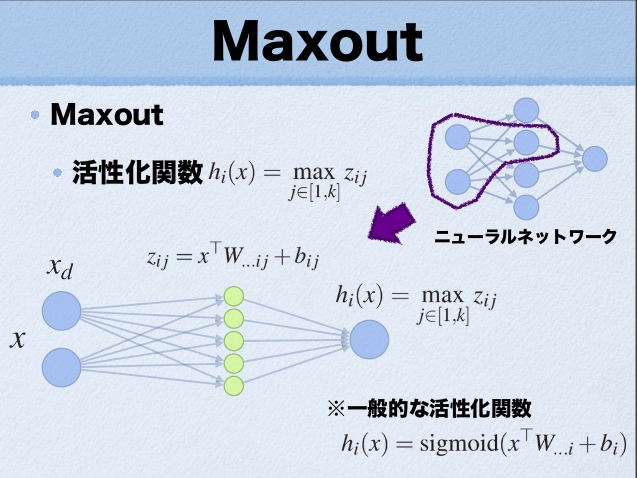
ppt中箭头前后示意图大家应该可以明白什么是maxout激发函数了。
maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。最直观的解释就是任意的凸函数都可以由分段线性函数以任意精度拟合(学过高等数学应该能明白),而maxout又是取k个隐隐含层节点的最大值,这些”隐隐含层"节点也是线性的,所以在不同的取值范围下,最大值也可以看做是分段线性的(分段的个数与k值有关)。论文中的图1如下(它表达的意思就是可以拟合任意凸函数,当然也包括了ReLU了):
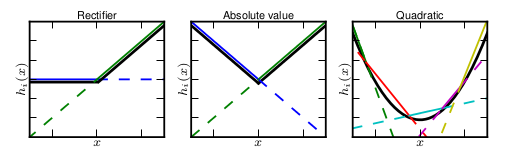
作者从数学的角度上也证明了这个结论,即只需2个maxout节点就可以拟合任意的凸函数了(相减),前提是”隐隐含层”节点的个数可以任意多,如下图所示:
下面来看下maxout源码,看其激发函数表达式是否符合我们的理解。找到库目录下的pylearn2/models/maxout.py文件,选择不带卷积的Maxout类,主要是其前向传播函数fprop():
def fprop(self, state_below): #前向传播,对linear分组进行max-pooling操作 self.input_space.validate(state_below) if self.requires_reformat: if not isinstance(state_below, tuple): for sb in get_debug_values(state_below): if sb.shape[0] != self.dbm.batch_size: raise ValueError("self.dbm.batch_size is %d but got shape of %d" % (self.dbm.batch_size, sb.shape[0])) assert reduce(lambda x,y: x * y, sb.shape[1:]) == self.input_dim state_below = self.input_space.format_as(state_below, self.desired_space) #统一好输入数据的格式 z = self.transformer.lmul(state_below) + self.b # lmul()函数返回的是 return T.dot(x, self._W) if not hasattr(self, 'randomize_pools'): self.randomize_pools = False if not hasattr(self, 'pool_stride'): self.pool_stride = self.pool_size #默认情况下是没有重叠的pooling if self.randomize_pools: z = T.dot(z, self.permute) if not hasattr(self, 'min_zero'): self.min_zero = False if self.min_zero: p = T.zeros_like(z) #返回一个和z同样大小的矩阵,元素值为0,元素值类型和z的类型一样 else: p = None last_start = self.detector_layer_dim - self.pool_size for i in xrange(self.pool_size): #xrange和reange的功能类似 cur = z[:,i:last_start+i+1:self.pool_stride] # L[start:end:step]是用来切片的,从[start,end)之间,每隔step取一次 if p is None: p = cur else: p = T.maximum(cur, p) #将p进行迭代比较,因为每次取的是每个group里的元素,所以进行pool_size次后就可以获得每个group的最大值 p.name = self.layer_name + '_p_' return p
仔细阅读上面的源码,发现和文章中描述基本是一致的,只是多了很多细节。
由于没有GPU,所以只用CPU 跑了个mnist的简单实验,参考:maxout下的readme文件。(需先下载mnist dataset到PYLEARN2_DATA_PATA目录下)。
执行../../train.py minist_pi.yaml
此时的.yaml配置文件内容如下:
!obj:pylearn2.train.Train { dataset: &train !obj:pylearn2.datasets.mnist.MNIST { which_set: 'train', one_hot: 1, start: 0, stop: 50000 }, model: !obj:pylearn2.models.mlp.MLP { layers: [ !obj:pylearn2.models.maxout.Maxout { layer_name: 'h0', num_units: 240, num_pieces: 5, irange: .005, max_col_norm: 1.9365, }, !obj:pylearn2.models.maxout.Maxout { layer_name: 'h1', num_units: 240, num_pieces: 5, irange: .005, max_col_norm: 1.9365, }, !obj:pylearn2.models.mlp.Softmax { max_col_norm: 1.9365, layer_name: 'y', n_classes: 10, irange: .005 } ], nvis: 784, }, algorithm: !obj:pylearn2.training_algorithms.sgd.SGD { batch_size: 100, learning_rate: .1, learning_rule: !obj:pylearn2.training_algorithms.learning_rule.Momentum { init_momentum: .5, }, monitoring_dataset: { 'train' : *train, 'valid' : !obj:pylearn2.datasets.mnist.MNIST { which_set: 'train', one_hot: 1, start: 50000, stop: 60000 }, 'test' : !obj:pylearn2.datasets.mnist.MNIST { which_set: 'test', one_hot: 1, } }, cost: !obj:pylearn2.costs.mlp.dropout.Dropout { input_include_probs: { 'h0' : .8 }, input_scales: { 'h0': 1. } }, termination_criterion: !obj:pylearn2.termination_criteria.MonitorBased { channel_name: "valid_y_misclass", prop_decrease: 0., N: 100 }, update_callbacks: !obj:pylearn2.training_algorithms.sgd.ExponentialDecay { decay_factor: 1.000004, min_lr: .000001 } }, extensions: [ !obj:pylearn2.train_extensions.best_params.MonitorBasedSaveBest { channel_name: 'valid_y_misclass', save_path: "${PYLEARN2_TRAIN_FILE_FULL_STEM}_best.pkl" }, !obj:pylearn2.training_algorithms.learning_rule.MomentumAdjustor { start: 1, saturate: 250, final_momentum: .7 } ], save_path: "${PYLEARN2_TRAIN_FILE_FULL_STEM}.pkl", save_freq: 1 }
跑了一个晚上才迭代了210次,被我kill掉了(笔记本还得拿到别的地方干活),这时的误差率为1.22%。估计继续跑几个小时应该会降到作者的0.94%误差率。
其monitor监控输出结果如下:
Monitoring step: Epochs seen: 210 Batches seen: 105000 Examples seen: 10500000 learning_rate: 0.0657047371741 momentum: 0.667871485944 monitor_seconds_per_epoch: 121.0 test_h0_col_norms_max: 1.9364999 test_h0_col_norms_mean: 1.09864382902 test_h0_col_norms_min: 0.0935518826938 test_h0_p_max_x.max_u: 3.97355476543 test_h0_p_max_x.mean_u: 2.14463905251 test_h0_p_max_x.min_u: 0.961549570265 test_h0_p_mean_x.max_u: 0.878285389379 test_h0_p_mean_x.mean_u: 0.131020009421 test_h0_p_mean_x.min_u: -0.373017504665 test_h0_p_min_x.max_u: -0.202480633479 test_h0_p_min_x.mean_u: -1.31821964107 test_h0_p_min_x.min_u: -2.52428183099 test_h0_p_range_x.max_u: 5.56309069078 test_h0_p_range_x.mean_u: 3.46285869357 test_h0_p_range_x.min_u: 2.01775637301 test_h0_row_norms_max: 2.67556467 test_h0_row_norms_mean: 1.15743973628 test_h0_row_norms_min: 0.0951322935423 test_h1_col_norms_max: 1.12119975186 test_h1_col_norms_mean: 0.595629304226 test_h1_col_norms_min: 0.183531862659 test_h1_p_max_x.max_u: 6.42944749321 test_h1_p_max_x.mean_u: 3.74599401756 test_h1_p_max_x.min_u: 2.03028191814 test_h1_p_mean_x.max_u: 1.38424650414 test_h1_p_mean_x.mean_u: 0.583690886644 test_h1_p_mean_x.min_u: 0.0253866100292 test_h1_p_min_x.max_u: -0.830110300894 test_h1_p_min_x.mean_u: -1.73539242398 test_h1_p_min_x.min_u: -3.03677525979 test_h1_p_range_x.max_u: 8.63650239768 test_h1_p_range_x.mean_u: 5.48138644154 test_h1_p_range_x.min_u: 3.36428499068 test_h1_row_norms_max: 1.95904749183 test_h1_row_norms_mean: 1.40561339238 test_h1_row_norms_min: 1.16953677471 test_objective: 0.0959691806325 test_y_col_norms_max: 1.93642459019 test_y_col_norms_mean: 1.90996961714 test_y_col_norms_min: 1.88659811751 test_y_max_max_class: 1.0 test_y_mean_max_class: 0.996910632311 test_y_min_max_class: 0.824416386342 test_y_misclass: 0.0114 test_y_nll: 0.0609837733094 test_y_row_norms_max: 0.536167736581 test_y_row_norms_mean: 0.386866656967 test_y_row_norms_min: 0.266996530755 train_h0_col_norms_max: 1.9364999 train_h0_col_norms_mean: 1.09864382902 train_h0_col_norms_min: 0.0935518826938 train_h0_p_max_x.max_u: 3.98463017313 train_h0_p_max_x.mean_u: 2.16546276053 train_h0_p_max_x.min_u: 0.986865505974 train_h0_p_mean_x.max_u: 0.850944629066 train_h0_p_mean_x.mean_u: 0.135825383808 train_h0_p_mean_x.min_u: -0.354841456 train_h0_p_min_x.max_u: -0.20750516843 train_h0_p_min_x.mean_u: -1.32748375925 train_h0_p_min_x.min_u: -2.49716541111 train_h0_p_range_x.max_u: 5.61263186775 train_h0_p_range_x.mean_u: 3.49294651978 train_h0_p_range_x.min_u: 2.07324073262 train_h0_row_norms_max: 2.67556467 train_h0_row_norms_mean: 1.15743973628 train_h0_row_norms_min: 0.0951322935423 train_h1_col_norms_max: 1.12119975186 train_h1_col_norms_mean: 0.595629304226 train_h1_col_norms_min: 0.183531862659 train_h1_p_max_x.max_u: 6.49689754011 train_h1_p_max_x.mean_u: 3.77637040198 train_h1_p_max_x.min_u: 2.03274038543 train_h1_p_mean_x.max_u: 1.34966894021 train_h1_p_mean_x.mean_u: 0.57555584546 train_h1_p_mean_x.min_u: 0.0176827309146 train_h1_p_min_x.max_u: -0.845786992369 train_h1_p_min_x.mean_u: -1.74696425227 train_h1_p_min_x.min_u: -3.05703072635 train_h1_p_range_x.max_u: 8.73556577905 train_h1_p_range_x.mean_u: 5.52333465425 train_h1_p_range_x.min_u: 3.379501944 train_h1_row_norms_max: 1.95904749183 train_h1_row_norms_mean: 1.40561339238 train_h1_row_norms_min: 1.16953677471 train_objective: 0.0119584870103 train_y_col_norms_max: 1.93642459019 train_y_col_norms_mean: 1.90996961714 train_y_col_norms_min: 1.88659811751 train_y_max_max_class: 1.0 train_y_mean_max_class: 0.999958965285 train_y_min_max_class: 0.996295480193 train_y_misclass: 0.0 train_y_nll: 4.22109408992e-05 train_y_row_norms_max: 0.536167736581 train_y_row_norms_mean: 0.386866656967 train_y_row_norms_min: 0.266996530755 valid_h0_col_norms_max: 1.9364999 valid_h0_col_norms_mean: 1.09864382902 valid_h0_col_norms_min: 0.0935518826938 valid_h0_p_max_x.max_u: 3.970333514 valid_h0_p_max_x.mean_u: 2.15548653063 valid_h0_p_max_x.min_u: 0.99228626325 valid_h0_p_mean_x.max_u: 0.84583547397 valid_h0_p_mean_x.mean_u: 0.143554208322 valid_h0_p_mean_x.min_u: -0.349097300524 valid_h0_p_min_x.max_u: -0.218285757389 valid_h0_p_min_x.mean_u: -1.28008164111 valid_h0_p_min_x.min_u: -2.41494612443 valid_h0_p_range_x.max_u: 5.54136030367 valid_h0_p_range_x.mean_u: 3.43556817173 valid_h0_p_range_x.min_u: 2.03580165751 valid_h0_row_norms_max: 2.67556467 valid_h0_row_norms_mean: 1.15743973628 valid_h0_row_norms_min: 0.0951322935423 valid_h1_col_norms_max: 1.12119975186 valid_h1_col_norms_mean: 0.595629304226 valid_h1_col_norms_min: 0.183531862659 valid_h1_p_max_x.max_u: 6.4820340666 valid_h1_p_max_x.mean_u: 3.75160795812 valid_h1_p_max_x.min_u: 2.00587987424 valid_h1_p_mean_x.max_u: 1.38777592924 valid_h1_p_mean_x.mean_u: 0.578550013139 valid_h1_p_mean_x.min_u: 0.0232071426066 valid_h1_p_min_x.max_u: -0.84151110053 valid_h1_p_min_x.mean_u: -1.73734213646 valid_h1_p_min_x.min_u: -3.09680505839 valid_h1_p_range_x.max_u: 8.72732563235 valid_h1_p_range_x.mean_u: 5.48895009458 valid_h1_p_range_x.min_u: 3.32030803638 valid_h1_row_norms_max: 1.95904749183 valid_h1_row_norms_mean: 1.40561339238 valid_h1_row_norms_min: 1.16953677471 valid_objective: 0.104670540623 valid_y_col_norms_max: 1.93642459019 valid_y_col_norms_mean: 1.90996961714 valid_y_col_norms_min: 1.88659811751 valid_y_max_max_class: 1.0 valid_y_mean_max_class: 0.99627268242 valid_y_min_max_class: 0.767024730168 valid_y_misclass: 0.0122 valid_y_nll: 0.0682986195071 valid_y_row_norms_max: 0.536167736581 valid_y_row_norms_mean: 0.38686665696 valid_y_row_norms_min: 0.266996530755 Saving to mnist_pi.pkl... Saving to mnist_pi.pkl done. Time elapsed: 3.000000 seconds Time this epoch: 0:02:08.747395
参考资料:
Maxout Networks. Ian J. Goodfellow, David Warde-Farley, Mehdi Mirza, Aaron Courville, Yoshua Bengio



