神经网络优化-动量梯度下降法(牛顿法)
背景
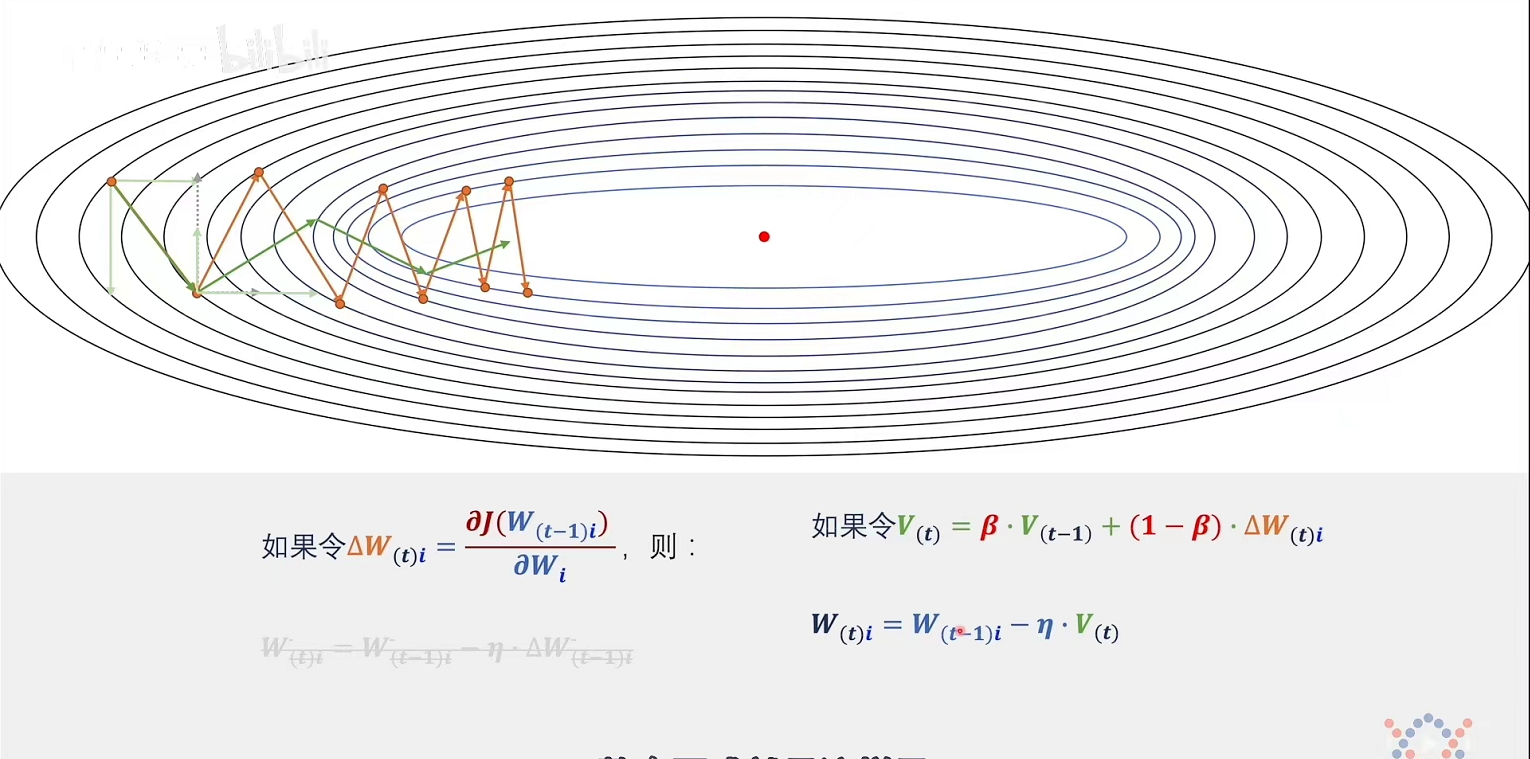
对于标准梯度下降过程，wt的更新是wt=wt-1+△w，而wt=wt-1-△w仅仅是对于当前点wt的△w，没有对于历史数据的考量（通俗点说叫经验教训）
结果就是下降（优化）过程前进方向速度缓慢，同时产生振荡（如图红线）
据此引入冲量v，令vt=vt-1-△w，由迭代思想知冲量v代表着从初始到当前△w的累积（即过程中对于各个纬度进行经验累积，具有经验教训的△w），并更新wt=wt-1-vt，则对于梯度下降有根据纬度的修正（前进方向促进，无效振荡方向削弱）
再进一步，由于当步数逐渐多了之后，前面的梯度和当前的梯度已有所区别，所以以往的梯度对当下的影响应该削弱，所以对v的构成进行加权，如图公式vt = βvt-1+(1-β)△w
另一个角度(正交分量--吴恩达)
由指数加权均值计算原理(https://www.cnblogs.com/toriyung/p/16535030.html)可知，梯度更新过程是对进行指数加权均值计算得出的dω进行更新。
在振荡方向，越靠近0梯度时(或者说时间越久)均值趋近0，即动量趋近0，则梯度更新量趋近于0；
前进方向一致，且均值保持不变或增大，梯度加速下降。
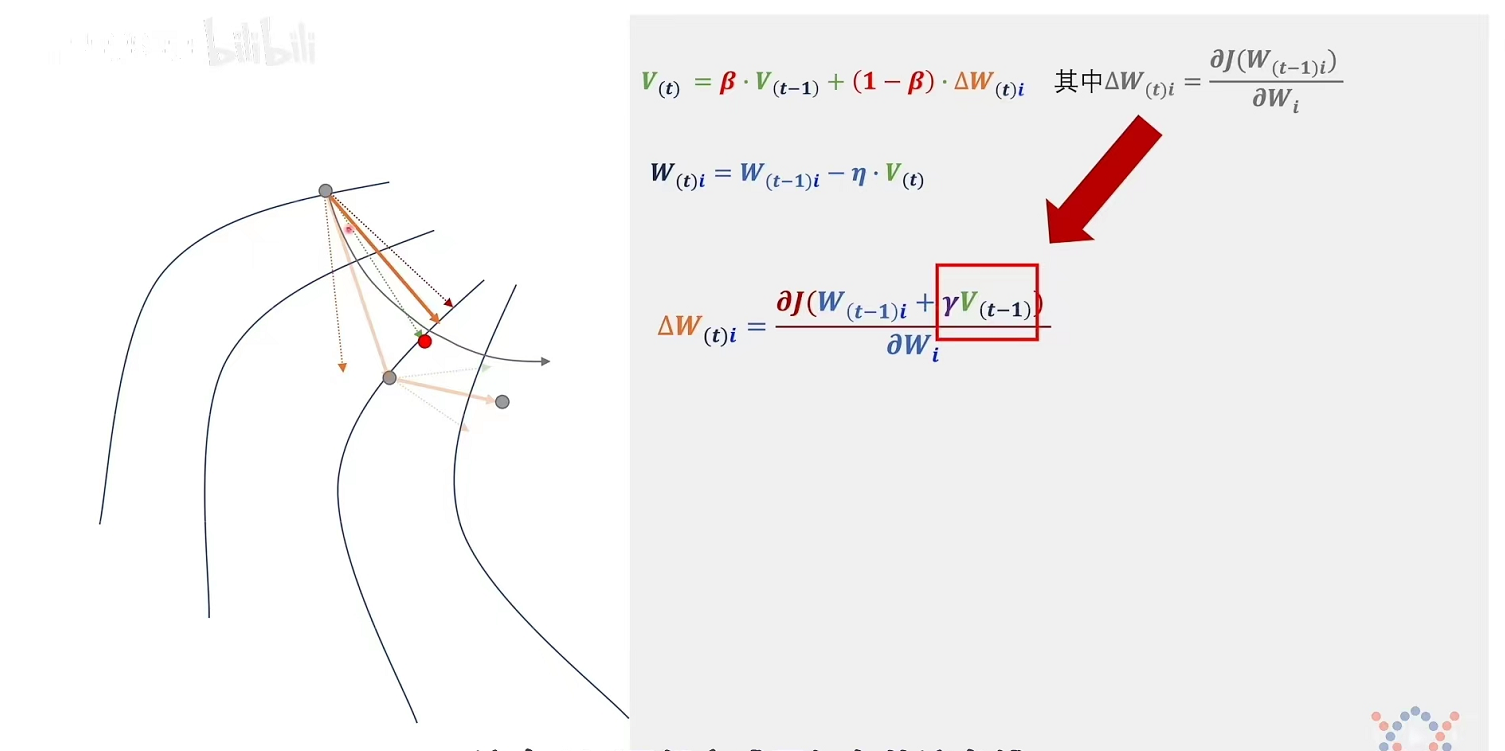
本来应对点w进行求导，但加入了代表惯性的冲量v进行求导，实现了超前的效果
