P2181 对角线

题面：

思考：
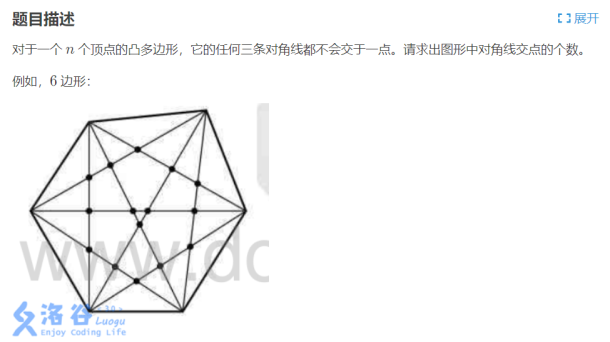
最初看到的时候就想到用组合数算对角线的公式，\(n\)边形有\(n\)个顶点，每两个顶点之间有一条对角线，六边形应该是\(C_6^2=\frac{6!}{2!4!}\)，然后数了数，发现自己想简单了，最起码也要减去边数，这么一推公式应该是\(\frac{n!}{2!(n-2)!}-n=\frac{n(n-1)}{2}-n=\frac{n(n-3)}{2}\)。接着考虑交点，最初的想法是任意三条对角线不相交与一点，也就是有三个交点，后来想到还存在交点是顶点的情况，这么一想还挺麻烦。看了题解有老哥说，从多边形顶点的角度来考虑，三条线相交有三个顶点的情况下一定有6个不同的顶点，再进一步观察就可以发现，一个对角线交点对应着两条没有重合顶点的对角线，也就是4个不同的顶点。所以，最终只需要计算\(C_n^4\)就可以了。然后考虑一下极端的情况，最少需要一个凸4变形，所以\(n\leqslant 3\)的时候是不行的。
代码：
数据还蛮大的，需要long long类型
用了long long还是爆了，又看了看题解说运算会爆，所以还得拆开来算，具体要这样n(n-1)/2(n-2)/3*(n-3)/4，nb的也可以上高精度

#include <stdio.h>

int main ()
{
    unsigned long long n;
    scanf("%lld",&n);
    if (n<4) {
        printf("0");
    } else {
        printf("%lld", n*(n-1)/2*(n-2)/3*(n-3)/4);
    }
    return 0;
}

第一次做这种题目，数学的部分远多于程序的部分，还挺有感触。