Chapter 1

复指数的性质

\(e^{j\theta}=cos\theta+jsin\theta\)

由此推出 \(cos\theta\) 是复数的实部，\(sin\theta\) 是指数的虚部，且对于任何模数为 \(1\) 的复数，

\[Re\{e^{j\theta}\}=cos\theta=\frac{e^{j\theta}+e^{-j\theta}}{2}\\ Im\{e^{j\theta}\}=sin\theta=\frac{e^{j\theta}-e^{-j\theta}}{2} \]

函数的拆分

任何函数都可以被唯一的拆分成一个奇函数和一个偶函数，即

\[x(t)=x_e(t)+x_o(t)\\ x_e(t)=\frac{1}{2}(x(t)+x(-t))\\ x_o(t)=\frac{1}{2}(x(t)-x(-t)) \]

假设有多种被拆分的形式，即 \(x(t)=f_1+g_1=f_2+g_2\) （其中 \(f\) 为奇函数， \(g\) 为偶函数），

那么 \(f_1-f_2=g_2-g_1\)

由于 奇函数 - 奇函数 = 奇函数，等式两边奇偶性相同，则 \(f_1-f_2=g_2-g_1=0\)

含有复数的指数、三角函数

指数函数

即 \(x(t)=e^{j\omega_0 t}\)

周期性：

\[x(t+T)=e^{j\omega_0 t}e^{j\omega_0T}=e^{j\omega_0 t}\\ e^{j\omega_0 T}=1\\ \omega_0T=2k\pi (k=\pm 1, \pm 2,\cdots) \\ T_0=\frac{2\pi}{|\omega_0|} \]

三角函数

由于 \(Ae^{j(\omega_0 t+\phi)}=Acos(\omega_0t+\phi)+Ajsin(\omega_0t+\phi)\) ，

\(Acos(\omega_0t+\phi)=\frac{A}{2}e^{j\phi}e^{j\omega_0t}+e^{-j\phi}e^{-j\omega_0t}\)

二者的周期是同步的

两种函数的能量

注意 \(e^{j\omega_0t}\) 是模长为 \(1\) 的复数，所以对于 \(e^{j\omega_0t}\) ，\(E_{period}=\int_0^{T_0}e^{j\omega_0t}dt=\int_0^{T_0}1dt=T_0\)

对于 \(Acos(\omega_0t+\phi)\) ，\(E_{period}=\int_0^{T_0}A^2cos^2(\omega_0t+\phi)dt\)

考虑 和差化积，\(cos^2\alpha=\frac{cos2\alpha + 1}{2}\)

\(E_{period}=\frac{A^2}{2}\int_0^{T_0}(1+cos(2\omega_0t+2\phi))dt=\frac{A^2}{2}T_0\)

指数函数产生的“谐波”

基波频率 \(\omega_0\) ，谐波频率是基波频率的 \(k\) 倍

震荡频率

对于指数函数和三角函数，当频率 \(\omega_0\) 从 \(0\) 到 \(\pi\) 震荡频率增大，从 \(\pi\) 到 \(2\pi\) 震荡频率减小

\(e.g. ~cos(\pi t)\) 的震荡频率大于 \(cos(\frac{3}{2}\pi t)\)

离散信号的周期性

对于连续信号来说，函数 \(e^{j\omega_0 t}\) 或 \(cos(\omega_0t+\phi)\) 的周期就是 \(\frac{2\pi}{\omega_0}\) ，而对于离散信号来说不一定是这样，举个例子：

\[x[n]=cos(\frac{4\pi n}{3}) \]

对于连续信号 \(x(t)=cos(\frac{4\pi t}{3})\) 来说，它的周期是 \(\frac{3}{2}\) ，

而对于离散信号来说， \(\frac{3}{2}\) 并不是信号上的点， \(x[n]\) 的周期是 \(N=m\frac{2\pi}{4\pi/3}的最小整数=3\)

离散信号的周期必须是整数，因此需要满足

\[\omega_0 N=2\pi m(m\in \mathbb Z)\\ N=\frac{2\pi m}{\omega_0},~s.t. N \in \mathbb Z^+ \]

脉冲信号与阶跃信号

离散信号

单位脉冲信号 \(\delta[n]=\left\{ \begin{matrix} 0,n\ne 0 \\ 1,n=0 \end{matrix} \right.\) ，单位阶跃信号 \(u[n]=\left\{ \begin{matrix} 0,n< 0 \\ 1,n\geq 0 \end{matrix} \right.\)

有如下性质：

\[\begin{align} \delta[n]&=u[n]-u[n-1]\\ u[n]&=\sum\limits_{k=\infty}^{0} \delta[n-k]\\ &=\sum\limits_{m=-\infty}^{n} \delta[m] \end{align} \]

对于任意离散信号 \(x[n]\) ，有：

\[x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0] \]

连续信号

单位阶跃信号 \(u(t)=\left\{ \begin{matrix} 0,t< 0 \\ 1,t> 0 \end{matrix} \right.\)

\[\begin{align} u(t)&=\lim_{\Delta \rightarrow 0}u_{\Delta}(t)\\ \delta_{\Delta}(t)&=\frac{d u_{\Delta}(t)}{dt} \\ \delta(t)&=\lim_{\Delta \rightarrow 0}(t)\\ u(t)&=\int_{-\infty}^{t} \delta(\tau)d\tau=\int_0^\infty \delta(t-\sigma)d\sigma\\ x(t)\delta(t-t_0)&=x(t_0)\delta(t-t_0) \end{align} \]

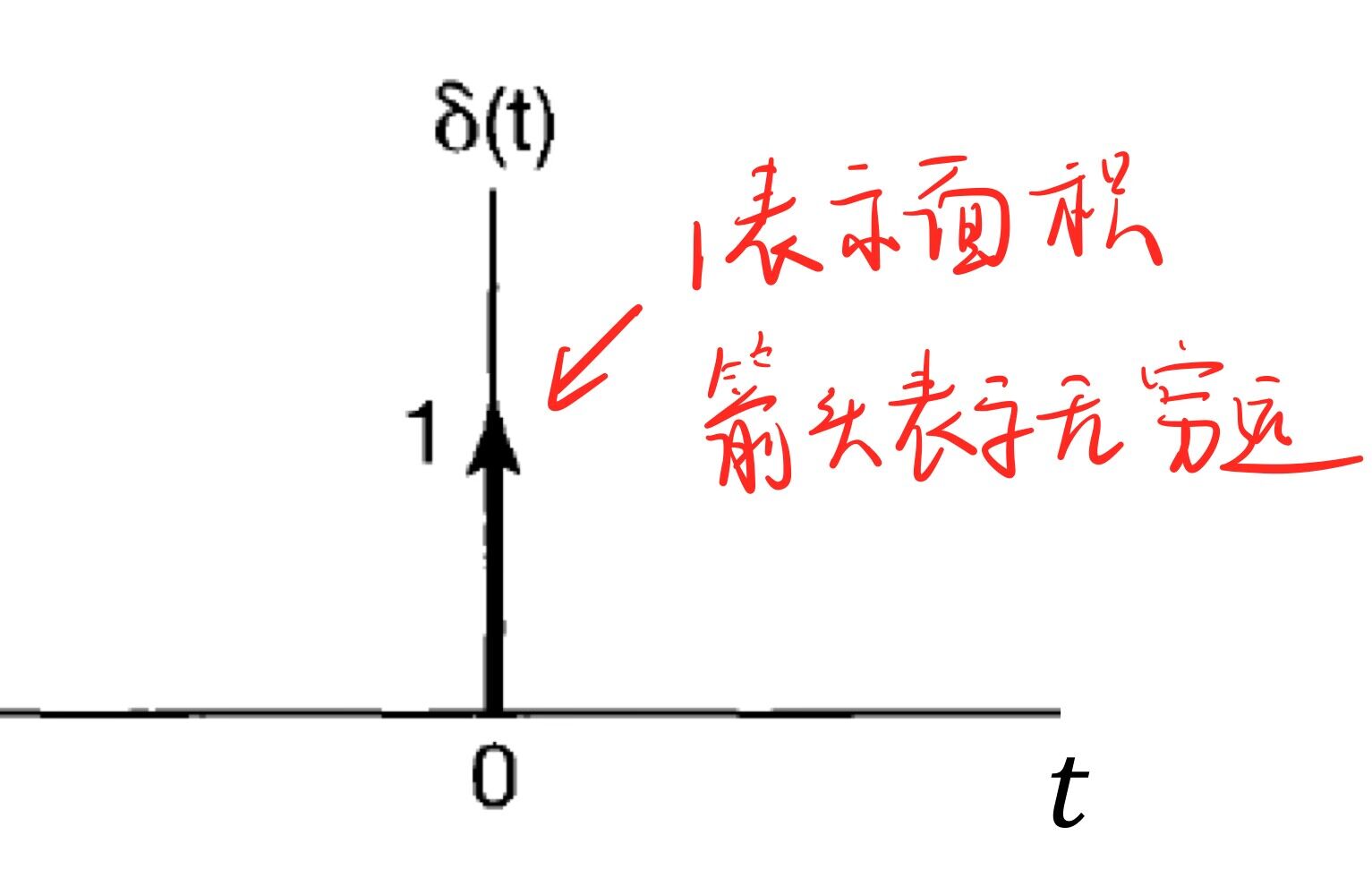
注意箭头表示无穷远，箭头的面积是 \(1\)

用脉冲信号和阶跃信号表示任意离散信号

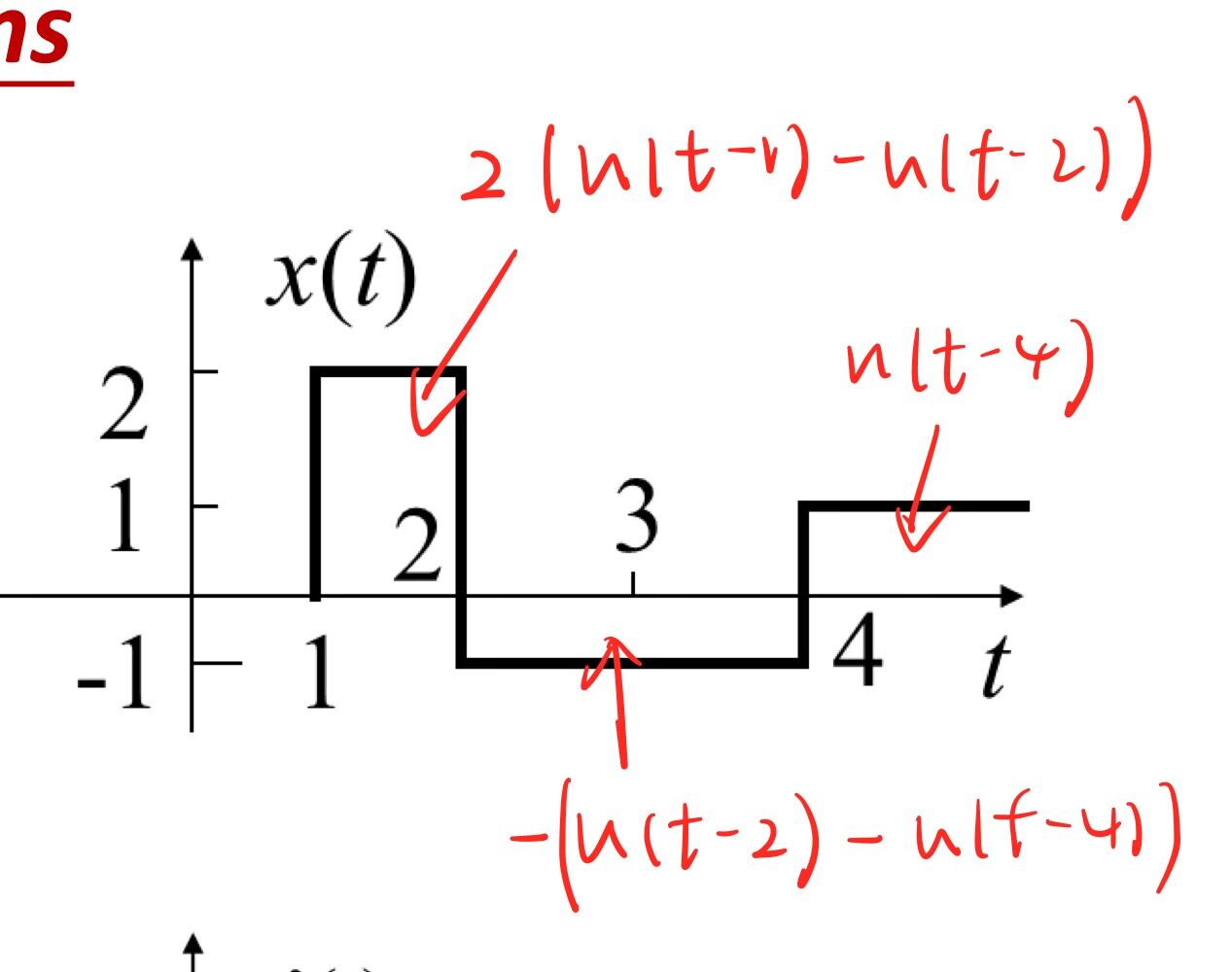
如图，\(x(t)=2u(t-1)-3u(t-2)+2u(t-4)\)
\(x'(t)=2\delta(t-1)-3\delta(t-2)+2\delta(t-4)\)

系统的基本性质

需要/不需要存储 (with/without memory)

只与当前时间有关，则不需要存储；否则需要存储

可逆性 (invertibility)

系统的 \(input\) 对 \(output\) 构成一个单射

因果性 (causality)

系统的 \(output\) 只与之前的时间值有关：

\(e.g.~y[n]=\sum\limits_{k=-\infty}^{n} x[k]\)

我的理解：如果出现该时间后的值，如 \(y[n]=x[n]-x[n+1]\) 。那么考虑如果 \(x[n]=y[n-1]\) ，那就寄了

相应的，如果是 \(y(t)=x(t)cos(t+1)\) 这种系统，就不会出现我理解的那种情况，那么是稳定的，也就属于因果系统了

稳定性 (stability)

有限的输入值得到有限的输出值

\(\underset{n\rightarrow \infty}{lim} x[n] \stackrel{LTI}{\rightarrow} y[n]\) ，则 \(y[n]\) 是有界的

时不变性 (time invariance)

如果系统 \(x[n] \stackrel{LTI}{\rightarrow} y[n]\) 满足时不变性，那么 \(x[n-n_0] \stackrel{LTI}{\rightarrow} y[n-n_0]\)

如果有和时间相关的系数，如 \(y[n]=(n-1)x[n]\) 那么时间轴发生变换肯定就不行了；

对于时间上的变化，时不变系统必须要求时间的线性性，不能存在翻转、放缩等等情况；

也就是说若 \(y[n]=kx[ax+b]\) ，那么 \(k\) 必须为常数，\(a\) 必须等于 \(1\)

线性性 (linearity)

如果系统1 \(x[n] \stackrel{LTI}{\rightarrow} y[n]\) 符合线性性，那么 \(ax_1[n] + bx_2[n] \stackrel{LTI}{\rightarrow} ay_1[n] + by_2[n]\)

用线性代数的思维想，符合线性变换（具有转换矩阵 \(\mathbb T\) ）的信号就具有线性性，如果出现常数项或大于一次的项，那么自然是不符合线性性的。

总结

性质	描述	符合的例子	不符合的例子
存储性 (memoryless)	是否只与当前时刻有关	\(y[n]=nx[n]\)	\(y[n]=x[n]+x[n-1]\)
可逆性 (invertibility)	是否能通过某种系统使得 \(y[n]\) 变回 \(x[n]\)	\(y[n]=\sum\limits_{k=-\infty}^{n} x[n]\)	\(y(t)=x^2(t)\) 或 \(y(t)=2x(t)+3\)
因果性 (causality)	任意时间点的 \(y[n]\) 只与之前的时间值有关	\(y[n]=\sum\limits_{k=-\infty}^{n} x[n]\)	\(y[n]=x[n]-x[n+1]\)
稳定性 (stability)	有限的输入得到有限的输出	\(y(t)=x^2(t)\)	\(y[n]=\sum\limits_{k=-\infty}^{n} u[n]\)
时不变性 (time invariance)	时间轴移动后输出不变	\(y[n]=sin(x[n])\)	\(y[n]=nx[n]\) 或 \(y[n]=x[-n]\)
线性性 (linearity)	符合线性变换的系统	\(y[n]=\sum\limits_{k=-\infty}^{n} x[n]\)	\(y[n]=sin(x[n])\)