2026.2.2校队集训笔记
参考文献:图论
定义
- 基本定义:图、阶、有向图、无向图、重边、自环。
- 相邻:相邻、邻域、邻边、出入边、度数,出入度
- 路径:途径、迹、回路、路径、环
- 联通:联通、强弱联通、强弱连通图、点双,边x双
- 特殊图:简单图、基图、有向无环图、完全图、树、稀疏稠密图
- 子图:子图、生成子图、导出子图,极大子图
DAG
topo sort
比较简单,每次删去一个没有入度的点,同时删去和这个点联通的边,然后再观察图中有没有没有入度的点就好了。
能被 \(topo \ sort\) 的图,被叫为 \(DAG\)。但有的时候一张图的 \(topo\) 序不止一个,叫做偏序。
欧拉路径/欧拉回路
判定
判定欧拉回路:有向图的话入度都要等于出度,无向图的话是度数要是偶数。
判定欧拉路径:有向图的话除了起始点入度比出度少一,终点的入度比出度多一,无向图是只有起始点和终点的度数是奇数,剩下的是偶数。
所有前提条件都是要图联通!!
求解
直接 \(dfs\) :对于有向图,对于一个点,如果这个点有出度,随便找到一个出边,先走过去,然后删掉这条边。对于无向图而言,直接随机选择一条边,走过去删掉即可。
两个的 \(dfs\) 都可以用类网络流的当前弧优化!!
特殊题型
混合图的欧拉路径
可以先给无向边定向,然后再跑欧拉路径,但是这样枚举的时间复杂太大了,不能手动给每一条边定向。
观察本质,对吼定向完之后应该是每一个点的出度要等于入度,只有起点和终点一个少了一个入度,一个多了一个入度,如果把度比作流把入度比作流入,把出度比作流出,这就是经典的最大流,直接跑就好了。
最短路
Bellman-Ford
松弛 \(n\) 轮,每轮把 \(m\) 条边松弛一边,可以证明,这样子松弛完之后就是最短路,时间复杂度 \(O(nm)\)。
以下是证明:
松弛的本质是一个点的最短路由另一个点的最短路扩展而来,一轮松弛可以更新一个点的最短路,两点之间的最短路一定最多只有 \(n-1\) 条边,所以更新 \(O(n)\) 轮就可以得到最短路。
SPFA
用队列优化 \(Bellman-Ford\) 的松弛过程,每次松弛最劣的最短路,理想时间复杂度是 \(O(n)\) ,但实际上极易被卡,会退化成 \(O(nm)\),所以很多选手都不会被使用。
这个算法的优点是可以用来判负环。
dijkstra
这个就不用说了,时间复杂度是 \(O(mlogm)\) 的,当稀疏图时,用优先队列优化,当是稠密图时,用暴力替代优先队列,时间复杂度变为 \(O(m)\)。
优化
当只有 \(01\) 边权的时候,可以把优先队列改成双端队列,如果松弛完之后是 \(0\) 就放队首,\(1\) 放队尾,可以优化掉优先队列的一只 \(log\)。
floyd
本质上是 \(dp\), 其他的最短路基本上本质都是贪心,这是他们之间比较大的区别。
时间复杂度 \(O(n^3)\) ,没人不会吧,由于他的 \(dp\) 特性,它可以求一些其他的特殊最短路问题
传递闭包
这跟 \(floyd\) 的 \(dp\) 特性没有一点关系,他是直接基于 \(floyd\) 加上 \(bitset\) 优化的,用于求两点之间的连通性,这个可以用 \(bitset\) 优化一下,时间复杂度就变成了 \(O(\frac{n^3}{w})\)。在赛场上这个 \(w = 8\) 有着关键的常数作用。
平面图最小割
- 平面图:可以通过不相交的直线和曲线画出来的图。
- 网格图:形成一个网格的平面图称为 网格图。
- 最小割: 断开一些边,使得起点和终点的被分开,这些被割开的边的权值和的最小值。
- 对偶图:如图,对偶图为平面图中的每一个面都有一个点(这里是红点),对于原图中的相邻两个面,作一条连接这两个面的红点的,只与这两个面边界相交的曲线(注意,两个面之间如果有两条边界,那么,要有两条新建的边)。
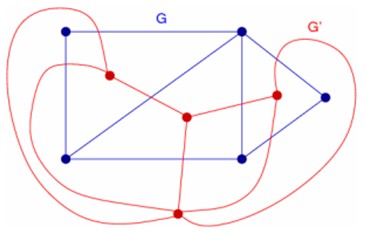
平面图最小割定理:平面图的最小割等于所对应的对偶图的最短路。
最小生成树
定义
生成树:点集为原图点集,边集为原图子集做形成的树(注意要是树!!)
最小生成树:生成出来的权值和最小的生成树。
Prim/kruskal
两个都是贪心思想,每次寻找能扩大连通块的最小权值的边,然后加入,再维护连通块即可。
两个算法不同的是,一个是合并若干个连通块,一个是不断往一个连通块里加新的点。
Boruvka
要先知道一个问题,在最小生成树上的任意一点,有一端是这个点的边权最小的边一定在最小生成树上,如果没有在最小生成树上,就加进去,然后会有一个有这个点的环,再删掉那条边权比较大的有一端是这个点的边,这时候生成树一定会更小。
这个算法就运用了这个性质:维护对于每个点,求出边权最小的邻边。将这些边删去后加入最小生成树,然后再将那个边权比较大的环上的边去掉,在合并连通块的同时保证边权最小,而且每次会删掉 \(O(\frac{n}{2})\) 的边,加入了 \(O(n)\) 的边,整体上在先前若干个连通块之间加上了 \(O(\frac{n}{2})\) 的边,连通块数量会严格减半,所以最多会有 \(O(long_2n)\) 次操作,时间复杂度很优。
注意在选择边权最小的边时,不能选择两端已经在同一连通块的边:
- 对每个点,选择一端为该点,另一端和它不在同一连通块的权值最小的边。
- 对每个连通块,选择一端在该连通块,另一端不在该连通块的权值最小的边。
连通分量
定义
- 割点:在无向图中,删去后使得连通分量数增加的点称为 割点。
- 割边:在无向图中,删去后使得连通分量数增加的边称为 割边,也称 桥。
- 点双连通图:不存在割点的无向连通图称为 点双连通图。根据割点的定义,孤立点和孤立边均为点双连通图。
- 边双连通图:不存在割边的无向连通图称为 边双连通图。根据割边的定义,孤立点是边双连通图,但孤立边不是。
- 点双连通分量:一张图的极大点双连通子图称为 点双连通分量(V-BCC),简称 点双。
- 边双连通分量:一张图的极大边双连通子图称为 边双连通分量(E-BCC),简称 边双。
- 点双连通:若
处于同一个点双连通分量,则称
点双连通。一个点和它自身点双连通。由一条边直接相连的两点也是点双连通的。 - 边双连通:若
处于同一个边双连通分量,则称
边双连通。一个点和它自身边双连通,但由一条边直接相连的两点不一定边双连通。
边双性质
- 两点之间任意一条迹上的所有割边,就是两点之间的所有必经边。
- 若 \(a\) 和 \(b\) 边双连通,\(b\) 和 \(c\) 边双连通,则 \(a\) 和 \(c\) 边双连通。
- \(u,v\) 边双连通当且仅当 \(u,v\) 之间没有必经边。
- 对于边双内任意一条边 \(u,v\),存在经过 \(u,v\) 的回路。
- 对于边双内任意一点 \(u\),存在经过 \(u\) 的回路。
点双性质
- 错误结论:两点之间任意一条路径上的所有割点,就是两点之间的所有必经点。
- 若两点双有交,那么交点一定是割点。
- 一个点是割点当且仅当它属于超过一个点双。
- 由一条边直接相连的两点点双连通。
- 一条边恰属于一个点双
tarjan
没啥好说的,记模板,过
瓶颈生成树/最小瓶颈路
这两个只要知道是什么意思就好了。
一个是这棵生成树上的最大边权最小,一个是这条路径上的最大边权最小。
最小生成树一定是瓶颈生成树,最短路一定是瓶颈最短路。
这就是一整个上午的所有内容,习题在上面的那个链接里。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号