五个题目池
由于看了某些学长的学习策略视频，某些人也要开始放仿造了qwq
五大题目池
1. 好题但还未筛选
2. 筛选完适合我，但是未看题解+按自己的想法来描述题解
- CF53E Dead Ends
- CF351C Jeff and Brackets
- CF442D Adam and Tree
- CF258D Little Elephant and Broken Sorting
- CF115E Linear Kingdom Races
3. 不想啃了，过
- Tree Decorations
- 基础寄术练习题
- 建造军营II
- Biconnected Graph
- 清明
- Mizuyokan 2
- Card Collection
- Security Guard
- Organizing a Race
- Mind Bloom
- Lisa's Sequences
- 三染色
- Bugaboo
- Colorful Star
- Attraction on Tree
- All the Same
4. 写完题解准备来打代码
-
-
考虑枚举 \(x,y\) 的 LCA，计算所有 \(LCA(x,y)=z\) 的 \(dist(x,y)\) 之和。不妨设 \(x\) 在 \(z\) 的左子树内，\(y\) 在 \(z\) 的右子树内\(（y\not=z）\)，则 \(x→y\) 的路径一定形如 \(x⇝a→b⇝y\)，其中 \(a\) 是 \(z\) 的祖先，\(b\) 在 \(y\) 的子树内，三段路径的形态分别形如：
- \(x⇝a\) 是一条由 \(x\) 只经过第一类边到达 \(a\) 的路径。显然此时一定不会去走第二类边。
- \(a→b\) 是一条二类边。
- \(b⇝y\) 是若干条一类边和二类边。
-
进一步发现，对于一个确定的 \(y\)，左侧的每个 \(x\) 到他要选择的这一条二类边 \(a→b\) 都是一样的。因此只需要在右侧跑 \(dijkstra\)，算出 \(a→b⇝y\) 这部分的贡献，再直接累加上 \(x⇝a\) 部分的贡献即可。
-
-
- 无穷条边，暴力 Kruskal 肯定不行。 每两点之间的边都取个 min 值，但是还是 \(O(n^2)\) 的，如果我们能把一些没用用的边去掉或者是把一些边改一下两端的点，那么复杂度就降低了。开始考虑改边，如果 \(x\) 和 \(y\) 已经联通，那么现在有一条边 \(x\) 和 \(z\)，可以改成 \(y\) 和 \(z\)。因为 \(a_i\) 和 \(b_i\) 在 \(a_i\) 和 \(b_{i+1}\) 前面已经出现过了, 那么 \(a_i\) 和 \(b_{i+1}\) 就可以改成 \(b_i\) 和 \(b_{i+1}\) 了！所以这变成了一条链,那么就可以用一个前缀和来做,然后跑 \(Kruskal\) 就好了
-
- 显然一个数如果被操作多次，只有最后一次有用。那么每个元素有三种情况：最后一次在放在开头，最后一次放到末尾，未操作过。前两种操作对应 a 的前缀后缀，中间剩余的元素必须是升序的。假设前缀有 x 个元素，后缀有 y 个元素，计数时先给每个操作划分到元素中，非最后一次的操作可以选方向，前缀操作和后缀操作内部有序，总的方案数就是：
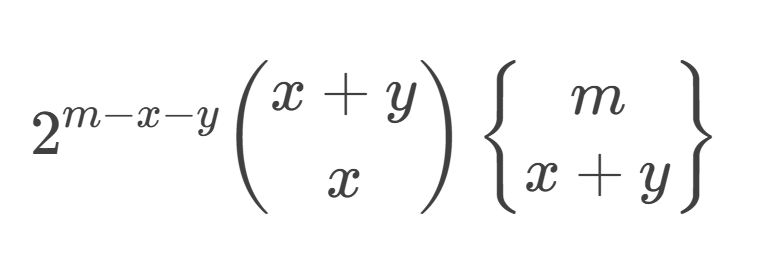然后就结束了qwq,预处理完之后 \(O(1)\) 即可
- 显然一个数如果被操作多次，只有最后一次有用。那么每个元素有三种情况：最后一次在放在开头，最后一次放到末尾，未操作过。前两种操作对应 a 的前缀后缀，中间剩余的元素必须是升序的。假设前缀有 x 个元素，后缀有 y 个元素，计数时先给每个操作划分到元素中，非最后一次的操作可以选方向，前缀操作和后缀操作内部有序，总的方案数就是：
-
- 为了简易，我们想办法使得最后只需要考虑取 \(w\) 体积的情况，这个可以通过对每一位加一些无价值节点实现。考虑从低位往高位依次计算。先考虑这一位内，若 \(w\) 这一位为 \(1\)，那么能取，直接取最大的即可。否则这一次是不能取的。剩下没用过的节点需要转移到更高一位，由于更高一位的一体积相当于当前位的两体积，因此我们需要给当前位所有元素两两打包。显然从大到小依次打包最优。于是这道题就贪心完了。
-
- 我们设 \(sum_i\) 表示 \(a_1⊕a_2⊕⋯⊕a_i\) ，则在 \(i\) 时刻 \(P⊕Q⊕R=sum_i\) ，且 \(P,Q,R\) 中有两个一样。那么一定是一个 \(sum_i\) 与两个相同的数，无序情况下形如 \((x,x,sum_i)\)。那么 \((x,x,sum_i)\) 由什么转移而来的？\((x,x,sum_i)←(sum_{i−1},sum_{i−1},sum_{i−1}⊕a_i),x=sum_{i−1}\) 。系数为
\(3\)。\((x,x,sum_i)←(sum_i,sum_i⊕a_i,sum_{i−1}),x=sum_{i−1}\)。系数为 \(2\)。那么用 \(map\) 来维护 \(dp_{i,j}\) 表示考虑了前 \(i\) 个数，\(x=j\) 的方案数。然后就 \(ok\) 了。
- 我们设 \(sum_i\) 表示 \(a_1⊕a_2⊕⋯⊕a_i\) ，则在 \(i\) 时刻 \(P⊕Q⊕R=sum_i\) ，且 \(P,Q,R\) 中有两个一样。那么一定是一个 \(sum_i\) 与两个相同的数，无序情况下形如 \((x,x,sum_i)\)。那么 \((x,x,sum_i)\) 由什么转移而来的？\((x,x,sum_i)←(sum_{i−1},sum_{i−1},sum_{i−1}⊕a_i),x=sum_{i−1}\) 。系数为
-
- 对于每个生成树是难以计算的，考虑计算当前的 \(a_i\) 会成为多少个边权。\(a_i\) 按 \(p\) 重新排列后，\(i\) 需要在前面选择一个父亲，则选择父亲的这条边的权值为 \(a_i\) 当且仅当前面的 \(k\) 个 \(a\) 中存在一个 \(a_j\) 使得 \(a_j≤a_j\)，其余的随便排。而 \(i\) 向儿子的全部连边中，边权为 \(a_i\) 当且仅当儿子 \(j\) 前面的 \(k\) 个 \(a\) 均比 \(a_j\) 大且 \(a_i\) 为最小的一个。则我们选出 \(k\) 个比 \(a_i\) 大的数进行排列并钦定这个排列右边的第一个数比 \(a_i\) 小即可。然后就做完了。
-
-
把 \(3^n\) 个儿子见到 \(3\) 叉 \(trie\) 上， 对于两个操作分讨
- \(Salasa\) ： 交换 \(1\), \(2\) 打懒标记
- \(Rumba\) : 轮换 \(0, 1, 2\)， \(0\), \(1\) 就直接换，\(2\) 要进位所以递归一下就好了
-
-
- 不太能数据结构维护，注意到值域小，对值域所有数处理对应的答案。发现如果 \(x,y\) 在某时刻的位置互为相反数，则它们此后的位置必为相反数。每次只维护符号相同区间 \([l,r]\)，若在当前操作后符号不完全相同了，则将符号不同的两边中元素数量较少的一边扔了——反正后面可以通过对称性得出；并对恰好可以取到 \(0\) 的位置打上标记。最后 \(dfs\) 一遍推出被扔掉的点的信息。
-
Guessing Permutation for as Long as Possible
- 限制等价于三点诱导子图有 \(\max(x→y, y→z) > x→z\) 。所以枚举有序三元组 \((x,y,z)\)，如果 \(\max((x,y), (x,z)) < (y,z)\)，则 \((x,y), (x,z)\) 定向时有且仅有一条是指向 $x￥ 的。发现顺便满足了 DAG，就是 \(2-sat\) 问题了。只要考虑个数，所以带权并查集即可。
-
- 二分答案，即要求每一段和小等 \(mid\), 能证明区间的数量是连续的。用树状数组优化 \(dp\) 求最多最少分几段就好了，这个东西你场上不会证明但是也不要心虚，一些贪心如果是比较经典的，就别证明了qwq
-
- 让⻥雷不动我们动，不能向下所以只能向左⼀格，向左上⼀格，由于状态是循环的，统计出以 12 为周期的⻥雷状态的⽅案数，⾏与⾏之间暴力就好了
-
- 首先 \([i/2^j]\ mod\ 2\) 表示子集 i 的二进制表示中第 j 位（从低到高）是否为 1。我们考虑数位dp，从⾼位到低位确定每个 \(x_i\)，然后四维背包记⼀下剩余容量，即还需满足的数值。可以发现的是，这个背包容量每维的容量不需要超过15，因为否则剩余的所有⼦集加起来也不够。进⼀步我们发现这个15是不紧的，⽐如对于⼀层，如果集合 1, 1234, 12, 134 都被⽤到了那么这两种⼀定能互相调整成更⼤的。可以⽤抽屉原理，简单证明这层最多⽤ 5 个，所以容量不会超过 9。
所以直接背包时间复杂度⼤概是 \(30 \times 10^4 \times 2^4\)，而实际上可以通过更仔细的分析，发现背包上界开到 7 也是⾜够的，但更⼩就不⾏了。
- 首先 \([i/2^j]\ mod\ 2\) 表示子集 i 的二进制表示中第 j 位（从低到高）是否为 1。我们考虑数位dp，从⾼位到低位确定每个 \(x_i\)，然后四维背包记⼀下剩余容量，即还需满足的数值。可以发现的是，这个背包容量每维的容量不需要超过15，因为否则剩余的所有⼦集加起来也不够。进⼀步我们发现这个15是不紧的，⽐如对于⼀层，如果集合 1, 1234, 12, 134 都被⽤到了那么这两种⼀定能互相调整成更⼤的。可以⽤抽屉原理，简单证明这层最多⽤ 5 个，所以容量不会超过 9。
-
- 暴力并查集显然不行，将下边界拓展到 b + 1，我们不用知道 1..b-1 的连通性，只需要知道第 b 行的就好了qwq，只维护第 b 行的并查集，发现维护的是后缀，所以就启迪我们去把等价的区间一块维护了，用分治解决就好了。
-
- 由于对称只看 \(a < b\), 对于长度为 \(len\) 的黑色长条， 前面的 \(len - (len mod k)\) 一定被经过，长度均为 \(k\), 把 \(len\) 看成 \(len mod k\) 即可，剩下的就能用特殊性质 \(c\) 来做了
-
- 只管父亲，儿子遇到就打标记，但是这样好像还是不行，因为这个的时间复杂度是 \(O(n \times d ^ 2)\), 发现只要让 \(\le d\) 的点最多被标记一次就好了，这样子的时间复杂度就降到了 \(O(n \times d)\).
-
- 度数小等 4， 把 i,i-1 去掉就最多剩下 7 个联通块,设 \(f_(i,p_1,p_2,S)\) 为 \(p_1\) 为 \(i-1\), \(p_2\) 为 \(i\), \(\le i\) 集合为 \(s\), 发现状态只有 \(n^2 \times 2^7\) 种，所以能过
-
-
记 \(f_{i,l,r}\) 为考虑值为 i 区间为 [l,r] 的方案，则
- $f_{i,l,r} ← I_{l,r} \times f_{i+1,l,r} 。
- $f_{i,l,r} ← \sum_{k∈[l,r]}I_{l,k−1} \times f_{i+1,l,k−1} \times f_{i,k+1,r} 。
-
-
- 等价于询问向量 (a,b)，对于前若干个向量，每个向量都要取偶数个，问能不能加起来得到向量 (c,d) 使得 c≤a,d≥b。（a,c 代表 \(\sqrt2\) 的系数，b,d 代表 −1 的系数）， 这个时候有一个偶数的限制就很烦，怎么办，全除掉就好了，猜：设最后一个向量是 (p,q)，只需要满足 \(p \div q \le a \div b\) 就行了。
-
-就是推柿子没什么好说的了，就是毒瘤推柿子题.....
-
- \(f_i=min(f_j+∑^{k=p_{j−1}}_j(c_k−i+1))\), 其中，其中 \(c_i\) 为第 i 个 A 前面有多少个 B,\(p_i\) 为最小的 \(k\) 使得 \(c_k−i\) 不为 0, 发现能够单调队列优化加斜率优化，就做完了
-
-
设 \(f_{l,r}\) 表示 \((l,r]\) 是原 \(a\) 序列，当前先手在 \(l\) 堆至少取多少石子能赢。设 \(g_{l,r}\) 表示 \([l,r)\) 是原 \(a\) 序列，当前后手在 \(r\) 堆至少取多少石子能赢。
- 当 \(l = l, f_{l, l} = 1\)
- 当 \(g_{l+1,r} > a_r, f_{l, r} = 1\)
- 当 \(g_{l+1,r} \le a_r, f_{l, r} = a_r - g_{l+1,r} + 1\)
- 当 \(l = l, g_{l, l} = 1\)
- 当 \(f_{l, r - 1} > a_l, g_{l, r}\)
- 当 \(f_{l, r - 1} \le a_l， g_{l,r} = a_l - f_{l, r - 1} + 1 + g_{l + 1, r}\)
-
-
- 只要正反两下就能只考虑周围的点qwq,设 \(c(u)\) 为 x 周围的点的个数，然后分讨
- topo内有一个数，中途记录出现在队列中的点的个数cnt,f[x]+=n−cnt
- topo内有两个数，记录队列中的两点x,y,对于y,如果y存在y−>z且z的入度为1,那么x显然不能到z,标记一下x即可
-
- 把上限锁死，要不然时间复杂度不稳定，因为一次一定就可以，但是答案一定是最大的，其实 \(|c_0, c_1|\) 不划算，不如拆开：\(∣c_0−c_1| =d\)调整为至多 \(d+1\) 次 \(c_0=c_1\), 想把 1 尽可能往后放，所以每次操作一个前缀是最优的。
-
- 首先，缩小范围，下界是不能都小于 0，否则答案肯定不超过 2n, 就考虑取正填负的策略就好了，为了更小，所以就不能重复走，我们分讨，如果我们走完这一段的前后缀，如果和 >0 我们就一定能够直接填完，否则要找前缀和大等 0的位置在分段操作，所以答案就是最大子段和，但是有参数不能直接维护，我们要用线段树来维护前缀和，这样子才能在合法时间内完成
-
- 把 \([l, r]\) 区间拆开，拆成 \([1, l]\), \([1, r]\)两块和跨 \(l, l-1\)的区间，前缀就建立 \(s_i\) 的 ACAM 以后把 t 拉上去跑，每走一步记录 fail 树上终止节点祖先的个数。至于跨越，就是建反串的 ACAM,然后放 fail 树上就好了
-
- wqs二分是我们看到题目的第一个想法，但是我们这个时间复杂度是 \(mnlog_w\) 再乘上阿尔法的这显然时间复杂度不对。。。。我们发现斜率有且仅且改变黑边。直接一起二分就好了，但是我们如果是偶数的话必定有一条不确定，我们就直接不管，去做 \(n-2\) 条边的最小生成树就好了qwq
-
， 就是求， 
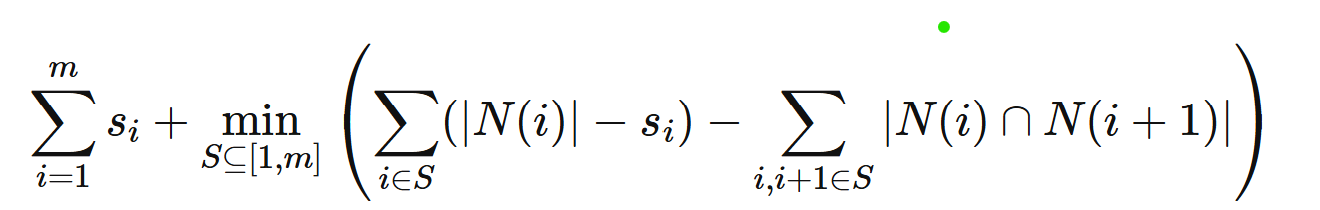，然后能用线段树维护
，这样子的一个鬼东东，区间内左右端点是否选择时的答案，这就是pushup，蚂蚁就单点修改，方糖就区间修改，
，对于选法的影响即 kx(k是区间个数)，\(x_r -x_l \le 2L\) ,所以在K=0的时候特判掉，时间复杂度 \(O(n\log_n)\)
-
- 考虑判断一个终止态是否可达,单个棋子必定可以到达，多个的话会产生多个连续段，把棋子看做成删除，要求是颜色要异于其他连续段的两边棋子的颜色。设第一个被删的段（最后一个放棋子的段）的最后一个棋子颜色为 c，必须在两边的是他的补色，所以把所有c的都删了，剩下只剩补集 c' , 所以含 c 的段就只有一个，所以这个段就是最后被删除的段（第一个放棋子的段），删棋子和放棋子的方案是一一对应的，所以合法删就是合法放，暴力dp,设 \(f_{i,0/1,0/1}\) 表示钦定 i 不放棋子，当前是否存在 第一个被删的段，当前是否存在 最后被删的段，放棋子数量的最小值。转移大概是如果 i−1 不放棋子就是 $f_{i,x,y}←f_{i−1,x,y}否则枚举 i−1 所在段的左端点，考虑这一段是第一个被删的段、最后被删的段还是其他段。时间复杂度是 \(O(n^2)\) ， 容易通过子序列自动机找到以 i−1 为右端点的第一个合法的左端点，并且发现能转移的点是一段前缀，这个前缀随着 i 增大而增大。分三类记一下前缀最小值即可,这样时间复杂度就降成 \(O(n)\) 了
-
AT_arc067_c [ARC067E] Grouping
- 设 \(f_{i,j}\) 代表分人数为 i 的组，当前有 j 个人的方案数，\(g_{i,k}\) 代表将 ki 个人分成 k 组，一组 i 个人的方案数。
,
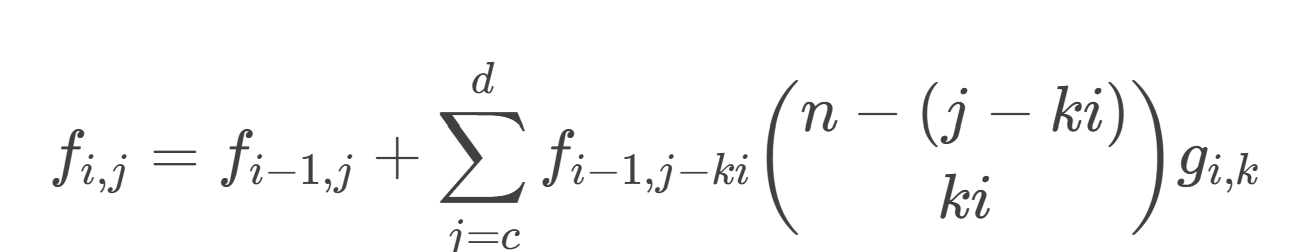,递推分子，枚举的是调和级数，所以是 \(O(n^2\long_n)\) 的时间复杂度.
- 设 \(f_{i,j}\) 代表分人数为 i 的组，当前有 j 个人的方案数，\(g_{i,k}\) 代表将 ki 个人分成 k 组，一组 i 个人的方案数。
-
AT_agc008_e [AGC008E] Next or Nextnext
- 全是相同的你就别管，可以证明一定是一个连通块，是颗内向基环树，考虑对于一个基环内向树如何还原 \(p_i\)，考虑记 i 点延长的链长为 L，i 点到前一个有延长链的环上节点距离为 L'，若 L>L′显然无解，若 L<L′则链顶可以选择放在 \(i−1→i\) 或 \(i−2→i−1\) 上，否则选择唯一。
剩下的就模拟讨论就好了qwq,时间复杂度 \(O(n\log_n)\)
- 全是相同的你就别管，可以证明一定是一个连通块，是颗内向基环树，考虑对于一个基环内向树如何还原 \(p_i\)，考虑记 i 点延长的链长为 L，i 点到前一个有延长链的环上节点距离为 L'，若 L>L′显然无解，若 L<L′则链顶可以选择放在 \(i−1→i\) 或 \(i−2→i−1\) 上，否则选择唯一。
-
- \(k_i = a_i - b_i\), \(x_i\) 为从 i 位置运送到 i+1 位置的壁的数量， 那么就有
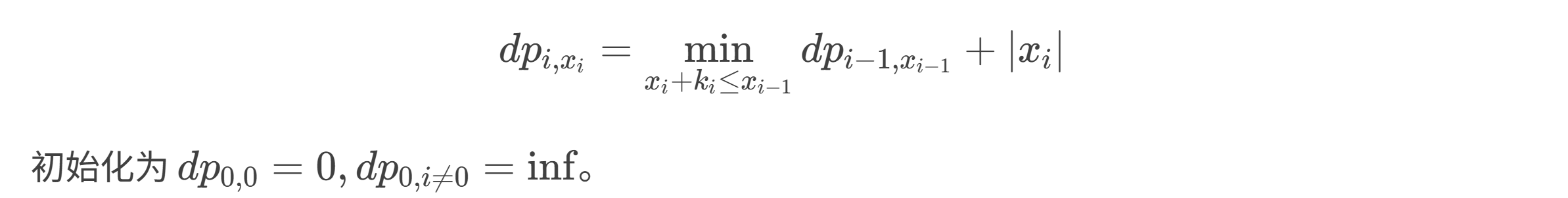
，这可以用slope trick 解决啊
- \(k_i = a_i - b_i\), \(x_i\) 为从 i 位置运送到 i+1 位置的壁的数量， 那么就有
-
，有后效性就把他二分出来（指 \(f_{1,H}\), H), 然后在二分，如果 \(f_{1,H} = mid\) 移动 l, 否则就移动 r. \(O(n^2)\) 的记忆化就结束了qwq
-
- 本来想着很复杂，一看题解，秒懂。。。。 记 \(f_{i, j}\) 示敲击了键盘 i 次，匹配了 j 个字符的方案数。有 \(f_{i,j}=(f_{i-1,max(j-1,0)}+f_{i-1,j+1} \times 2)\) ， 然后注意一下边界就好了哇
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 3010;
const int mod = 1e9 + 7;
int n;
string str;
int f[N][N];
signed main()
{
cin >> n >> str;
f[0][0] = 1;
for (int i = 1 ; i <= n ; i ++ )
for (int j = 0 ; j <= i ; j ++ )
f[i][j] = (f[i - 1][max(j - 1, 0ll)] + f[i - 1][j + 1] * 2 % mod) % mod;
cout << f[n][str.size()]<<endl;
return 0;
}
-
AT_agc043_d [AGC043D] Merge Triplets
- 最终的排列中，按照前缀 max 的位置划分，每一段的长度不超过 3，这是必要条件但是好像不充分，长度为 2 的段个数不超过长度为 1 的段个数。好像充要。所以设 \(f_{i,j}\) 表示考虑前 i 个数，长度为 1 的段个数减去长度为 2 的段个数为 j 的方案数。枚举的时候枚举长度就好了，时间复杂度 \(O(n^2)\)
-
AT_agc041_d [AGC041D] Problem Scores
- 这不就等价于，有 n 种物品，每一种都有无限个，第 i 种物品重量为 \(w_i\)，现在要选出一些物品使得总重不超过 n−1，求方案数。很简单的无限背包
-
AT_agc040_e [AGC040E] Prefix Suffix Addition
- 记 \(dp_{i,j}\) 表示我们在第 i 个数令了 \(q_i=j\)。容易发现 DP 转移：
- 把 \(a_i−a_{i−1}\) 按正负分讨就好了
-
AT_agc022_e [AGC022E] Median Replace
- 维护一个从栈底到栈顶由一段连续的 1 和一段连续的 0 组成的栈。
- 若 c = 0 着必定赚翻了，三个成一个 0 他不香吗
- 若 c = 1 ， 是 0 就抵消了（指栈顶，两个1就忽略掉就好了啊，否则就要多加一个1
-
P4931 [MtOI2018] 情侣？给我烧了！（加强版）
- 这就是一个简单的母函数模板，推出来就是 \((i+1) \times f_{i+1}=4 \times i \times f_i + 8 \times f_{i−1}\)， 然后预处理就好了
-
- 这道题目还是生成函数，只不过推完之后还有一点的求通项，然后直接带入就好了
- \(a_n≡485071604×940286408^n+514928404×59713601^n(mod10^9+7)\)
-
- 这不就是板子吗，就是有点卡常，这个预处理的长度最好是 \(2 \times 10^7\)
-
[P6860 象棋与马](https://www.luogu.com.cn/problem/P6860）
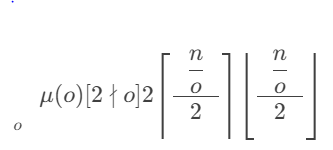，没掉的是求和，这个的话有意思，推的过程有亿点点长，放不下，然后再把这个套杜教筛就好了呢
-
- 这还要讲吗，狄利克雷板子，做一下类似埃筛就好了
-
P12939 [NERC 2019] Foolprüf Security
- 黑白染色，最终 Prüfer 序列里一定有 n−1 个白点（删了这么多黑点）和 m−1 个黑点（删了这么多白点）。， 所以无解的一个充分条件：\(k_a≥m\) 或 \(k_b≥n\), 剩下的就按模板构造就好了
-
- 把 \(L, K\) 闲着没事除个 \(K\), 这不就成了选数N次使选出的数最大公约数为1的方案数。f[i]实际上是含有公约数i的方案数，然后用一下容斥，f[i]分别减去f[2i],f[3i] ， 倒着推一遍就好了，\(L = 1\) 的时候要特判
- 就是先Dfs染一遍色, 黑节点的儿子是白点，白点的儿子是黑点, 然后用 f[i][j] 来表示i这个点为j方赢时最少控制的关键节点,数
- 若是黑点，如果该点是白点，则只有其所有的儿子都是黑节点，如果该点是黑点，则只需要有一个儿子是黑点，白点亦然
- 再Dfs一遍，合并了就好了
-
5. 答案代码了（由于啥也没用，所以不算题目池qwq
浙公网安备 33010602011771号