2025.8.15校队题单分享+总结
T1
Cow at Large G
题目描述
最后,Bessie 被迫去了一个远方的农场。这个农场包含 \(N\) 个谷仓(\(2 \le N \le 10^5\))和 \(N-1\) 条连接两个谷仓的双向隧道,所以每两个谷仓之间都有唯一的路径。每个只与一条隧道相连的谷仓都是农场的出口。当早晨来临的时候,Bessie 将在某个谷仓露面,然后试图到达一个出口。
但当 Bessie 露面的时候,她的位置就会暴露。一些农民在那时将从不同的出口谷仓出发尝试抓住 Bessie。农民和 Bessie 的移动速度相同(在每个单位时间内,每个农民都可以从一个谷仓移动到相邻的一个谷仓,同时 Bessie 也可以这么做)。农民们和 Bessie 总是知道对方在哪里。如果在任意时刻,某个农民和 Bessie 处于同一个谷仓或在穿过同一个隧道,农民就可以抓住 Bessie。反过来,如果 Bessie 在农民们抓住她之前到达一个出口谷仓,Bessie 就可以逃走。
Bessie 不确定她成功的机会,这取决于被雇佣的农民的数量。给定 Bessie 露面的谷仓K,帮助 Bessie 确定为了抓住她所需要的农民的最小数量。假定农民们会自己选择最佳的方案来安排他们出发的出口谷仓。
输入格式
输入的第一行包含 \(N\) 和 \(K\)。接下来的 \(N - 1\) 行,每行有两个整数(在 \(1\sim N\) 范围内)描述连接两个谷仓的一条隧道。
输出格式
输出为了确保抓住 Bessie 所需的农民的最小数量。
输入输出样例 #1
输入 #1
7 1
1 2
1 3
3 4
3 5
4 6
5 7
输出 #1
3
先模拟一下样例:
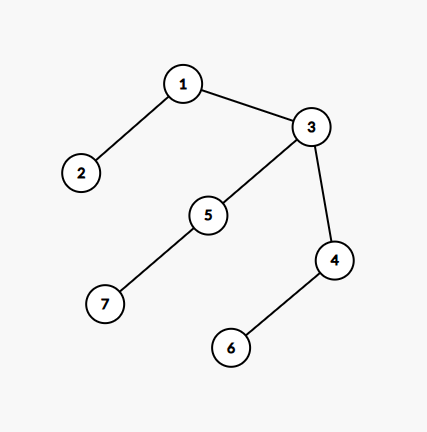
我们在叶子节点上放三个农民,分别在 \(2\), \(6\), \(7\) 上,刚开始是这样的:

接着因为 \(2\) 号点上有农民,所以 \(Bessie\) 只能去 \(3\), 最后:

\(Bessie\) 被困死了,综上三个村民是可行的,我们也可以证明两个村民是不行的,详见其他题解区,我们怎么正向的去做这道题呢,我们的村民一定是从叶子走到根的(这里的树是以 \(k\) 为根的)这样子能缩包围圈,所以一定可行,那我们一定可以有更优解,具体考虑从叶子节点不断标记,直到遇到 \(Bessie\), 接下来 \(Bessie\) 走到的被标记的点的个数就是能困住他的需要的最少的农民个数,这个东西就感性理解就好,主要是我自己也不太会证,这个打标记的做法有很多种,我用的是遍历两次,第一次记录父节点,第二次暴力往上推就好了,其他的题解还给了下面两种方法:
-
在第一遍遍历的时候用一个栈记录路径,每次找到叶子节点就在栈顶的位置 \(\times 0.5\) 处的节点做标记。
-
在第一遍遍历的时候记录一个 \(down\) 数组表示离这里最近的叶子节点的距离。在第二遍遍历的时候,如果当前的深度 ≥ 当前节点的 \(down\) 值,就算遇到了标记。
给一个代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const int M = N << 1;
int n, k;
int p[N], deep[N] = {-1}, ans;
bool vis[N], st[N];
int h[N], e[M], ne[M], idx;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs1(int u, int fa)
{
vis[u] = 1;
p[u] = fa;
deep[u] = deep[fa] + 1;
for(int i = h[u] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(j == fa) continue;
vis[u] = 0;
dfs1(j, u);
}
}
void dfs2(int u, int fa)
{
if(st[u])
{
ans ++ ;
return;
}
for(int i = h[u] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(j == fa) continue;
dfs2(j, u);
}
}
int main()
{
cin >> n >> k;
p[k] = 0;
memset(h, -1, sizeof h);
for(int i = 1 ; i < n ; i ++ )
{
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
dfs1(k, 0);
for(int i = 1 ; i <= n ; i ++ )
if(vis[i])
{
int tmp = i;
for(int j = 1 ; j <= deep[i] / 2 ; j ++ ) tmp = p[tmp];
st[tmp] = 1;
}
dfs2 (k, 0);
cout << ans;
return 0;
}
T2
P9017 [USACO23JAN] Lights Off G
题目描述
给定正整数 \(N\),和两个长为 \(N\) 的 \(01\) 序列 \(a\) 和 \(b\)。定义一次操作为:
- 将 \(b\) 序列中的一个值翻转(即 \(0\) 变成 \(1\),\(1\) 变成 \(0\),下同)。
- 对于 \(b\) 序列中每个值为 \(1\) 的位置,将 \(a\) 序列中对应位置的值翻转。
- 将 \(b\) 序列向右循环移位 \(1\) 位。即若当前 \(b\) 序列为 \(b_1b_2\cdots b_{n}\),则接下来变为 \(b_{n}b_1b_2\cdots b_{n-1}\)。
有 \(T\) 次询问,对每一次询问,你需要回答出至少需要几次操作,才能使 \(a\) 序列中每一个位置的值都变为 \(0\)。
输入格式
第一行为两个正整数 \(T,N\;(1\leq T\leq 2\times10^5,2\leq N\leq 20)\)。
接下来 \(T\) 行,每行为两个长为 \(N\) 的 \(01\) 序列 \(a\) 和 \(b\),表示一组询问。
输出格式
共 \(T\) 行,每行一个正整数,表示最少的操作次数。
输入输出样例 #1
输入 #1
4 3
000 101
101 100
110 000
111 000
输出 #1
0
1
3
2
输入输出样例 #2
输入 #2
1 10
1100010000 1000011000
输出 #2
2
若某一答案为 \(k\),我们可以先把 \(b\) 中每个 \(1\) 可以改变的 \(k\) 个位置反转,然后第 \(i\) 次操作就只改变了它后的 \(k−i+1\) 位的状态。所以问题转化为给一个二进制串,问是否能 \(k\) 次操作给他变成全零。用状压 DP \(O(n^2 \times 2^n)\) 预处理,之后对于每一组询问枚举判断就好了,总时间复杂度 \(O(T \times n^2 + n^2 \times 2^n)\)。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
int T, n;
int g[45][22], mask[22];
bool f[45][1 << 21];
string s, t;
int calc(int s, int t)
{
if(s == 0) return 0;
for(int i = 1 ; i <= 2 * n ; i ++ )
{
int vis = s;
for(int j = 0 ; j < n ; j ++ )
if(t & (1 << j))
vis = vis ^ g[i][j];
if(f[i][vis]) return i;
}
}
signed main()
{
f[0][0] = 1;
cin >> T >> n;
for (int i = 0 ; i <= n ; i ++ ) mask[i] = 1 << i;
int N = 1 << n;
for(int k = 0 ; k < n ; k ++ )
for(int i = 1; i <= 2 * n ; i ++ )
for(int j = 0; j < i ; j ++ )
g[i][k] ^= mask[(k + j) % n];
for(int i = 1 ; i <= 2 * n ; i ++ )
for(int j = 0 ; j < N ; j ++ )
{
if(!f[i - 1][j]) continue;
for(int k = 0 ; k < n ; k ++ )
{
int vis = j;
vis ^= g[i][k];
f[i][vis] = 1;
}
}
while (T --)
{
cin >> s >> t;
int S = 0, T = 0;
for(int i = 0 ; i < n ; i ++ )
{
if (s[i] == '1') S ^= (1 << i);
if (t[i] == '1') T ^= (1 << i);
}
cout << calc(S, T) << endl;
}
return 0;
}
T3
P9016 [USACO23JAN] Find and Replace G
题目描述
你有一个字符串 \(S\),最开始里面只有一个字符 \(\text{a}\),之后你要对这个字符串进行若干次操作,每次将其中每一个字符 \(c\) 替换成某个字符串 \(s\)(例如对于字符串 \(\text{ball}\),将其中的 \(\text{l}\) 替换为 \(\text{na}\) 后将会变为 \(\text{banana}\))。现在给定 \(l,r\),你需要输出 \(S_{l\ldots r}\)(也就是 \(S\) 的第 \(l\) 个字符到第 \(r\) 个字符对应的子串)是什么。
输入格式
第一行三个整数,分别表示 \(l,r\) 和操作次数。
输出格式
一行,表示对应的子串。
输入输出样例 #1
输入 #1
3 8 4
a ab
a bc
c de
b bbb
输出 #1
bdebbb
说明/提示
\(l,r\le\min(\left | S \right |,10^{18})\);
\(r-l+1\le2\times10^5\);
\(\sum\left | s \right | \le 2\times 10^5\)。
所有的字符串都只包含小写字母 \(\text{a}-\text{z}\)。
其中对于测试点 \(2-7\),满足:
\(r-l+1\le2000\),\(\sum\left | s \right | \le 2000\)。
设 \(f_{i,j}\) 为第 \(i\) 时间,以字符 \(j\) 展开之后的字符,然后暴力展开,考虑一下优化:
- 首先就是记忆化
- 小于 \(l\) 跳过
- 大于 \(r\) 直接输出,程序结束
这样就做完啦,简单粗暴,比别人的都简单~~
给个代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 110;
const int K = 30;
int n;
int L, R;
int e[N][K], p[N][K];
int size_[N][K];
string s[N];
void build()
{
for(int r = 0 ; r < K ; r ++ ) e[n + 1][r] = n + 1, size_[n + 1][r] = 1, p[n + 1][r] = n + r + 1;
for(int i = n ; i >= 1 ; i -- )
{
for(int r = 0 ; r < K ; r ++ )
{
if(e[i][r] == 0) p[i][r] = n + r + 1, e[i][r] = i + 1;
for(char& ch : s[p[i][r]]) size_[i][r] = min((int)1e18, size_[i][r] + size_[e[i][r]][ch - 'a']);
}
}
}
int now = 0;
char ans[N], *tmp = ans;
void print(int r)
{
*tmp++ = r + 'a';
if(++now >= R) cout << ans << endl, exit(0);
}
char *st[N][K], *ed[N][K];
void dfs(int u, int r)
{
if(now + size_[u][r] < L)
{
now += size_[u][r];
return;
}
if(st[u][r])
{
for(char* p = st[u][r] ; p != ed[u][r] ; p ++ ) print(*p - 'a');
return;
}
if(now >= L) st[u][r] = tmp;
if(u == n + 1) print(r);
else for(char& ch : s[p[u][r]]) dfs(e[u][r], ch - 'a');
ed[u][r] = tmp;
}
signed main()
{
cin >> L >> R >> n;
for(int i = 1 ; i <= n ; i ++ )
{
char ch;
cin >> ch >> s[i];
e[i][ch - 'a'] = i + 1;
p[i][ch - 'a'] = i;
}
for(int i = n + 1 ; i <= n + 26 ; i ++ ) s[i] = i - n - 1 + 'a';
build();
dfs(1, 0);
cout << ans;
return 0;
}
P11843 [USACO25FEB] The Best Subsequence G
题目描述
Farmer John 有一个长为 \(N\) 的位串(\(1 \leq N \leq 10^9\)),初始时全部为零。
他将首先按顺序对字符串执行 \(M\) 次更新(\(1 \leq M \leq 2 \cdot 10^5\))。每次更新会翻转从 \(l\) 到 \(r\) 的每个字符。具体地说,翻转一个字符会将其从 \(0\) 变为 \(1\),或反之。
然后,他会进行 \(Q\) 次查询(\(1 \leq Q \leq 2 \cdot 10^5\))。对于每个查询,他要求你输出由从 \(l\) 到 \(r\) 的子串中的字符组成的长为 \(k\) 的字典序最大子序列。如果你的答案是一个位串 \(s_1s_2 \dots s_k\),则输出 \(\sum_{i=0}^{k-1} 2^i \cdot s_{k-i}\)(即将其解释为二进制数时的值)模 \(10^9+7\) 的余数。
一个字符串的子序列是可以从中通过删除一些或不删除字符而不改变余下字符的顺序得到的字符串。
我们知道,字符串 \(A\) 的字典序大于长度相等的字符串 \(B\),当且仅当在第一个 \(A_i \neq B_i\) 的位置 \(i\) 上(如果存在),我们有 \(A_i > B_i\)。
输入格式
输入的第一行包含 \(N\),\(M\) 和 \(Q\)。
以下 \(M\) 行,每行包含两个整数 \(l\) 和 \(r\)(\(1 \leq l \leq r \leq N\)),为每次更新的端点。
以下 \(Q\) 行,每行包含三个整数 \(l\),\(r\) 和 \(k\)(\(1 \leq l \leq r \leq N\),\(1 \leq k \leq r - l + 1\)),为每个查询的端点和子序列的长度。
输出格式
输出 \(Q\) 行。第 \(i\) 行包含第 \(i\) 个查询的答案。
输入输出样例 #1
输入 #1
5 3 9
1 5
2 4
3 3
1 5 5
1 5 4
1 5 3
1 5 2
1 5 1
2 5 4
2 5 3
2 5 2
2 5 1
输出 #1
21
13
7
3
1
5
5
3
1
输入输出样例 #2
输入 #2
9 1 1
7 9
1 8 8
输出 #2
3
输入输出样例 #3
输入 #3
30 1 1
1 30
1 30 30
输出 #3
73741816
说明/提示
样例 1 解释:
在执行 \(M\) 次操作后,位串为 \(10101\)。
对于第一个查询,长度为 \(5\) 的子序列仅有一个,\(10101\),其解释为 \(1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 21\)。
对于第二个查询,长度为 \(4\) 的不同的子序列有 \(5\) 个:\(0101\),\(1101\),\(1001\),\(1011\),\(1010\)。字典序最大的子序列为 \(1101\),其解释为 \(1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1\cdot 2^0 = 13\)。
对于第三个查询,字典序最大的序列是 \(111\),其解释为 \(7\)。
样例 3 解释:
确保输出答案对 \(10^9+7\) 取模。
- 测试点 \(4\):\(N \leq 10, Q \leq 1000\)。
- 测试点 \(5\):\(M \leq 10\)。
- 测试点 \(6\sim 7\):\(N, Q \leq 1000\)。
- 测试点 \(8\sim 12\):\(N \leq 2 \cdot 10^5\)。
- 测试点 \(13\sim 20\):没有额外限制。
先离线用类似差分处理,得到极长 \(0\) 与极长 \(1\) 。一个贪心:先加尽可能多的 \(1\),如果没有 \(1\) 了,那就从右往左找 \(0\) 加,可以证明这是最优的。考虑最后的答案形成一个结构:一个 \(1\) 块后缀,数个 \(1\) 整块,一个 \(0\) 块前缀,由 \(0\) 整块与 \(1\) 整块构成的一个大块,一个 \(0\) 块或 \(1\) 块后缀。先判 \(l,r\) 在同一块的情况。按块做 \(1\) 数量前缀和,处理 \(1\) 数量超过 \(k\) 的情况。按块做后缀转十进制的结果,可以求任意块间的二进制串的值。按块做 \(0\) 数量后缀和,用二分找到 \(0\) 块前缀所在块编号,注意当 \(r\) 位于 \(0\) 块时有细节。根据这个编号就可以求出由 \(0\) 整块与 \(1\) 整块构成的大块的值。把答案拼一起即可,时间复杂度 \(O((m+q) \times log_n)\)。
代码如下:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5 + 10;
const int p = 1e9 + 7;
int n, m, q, k;
int L[N], w[N], c[N];
int s[N], tmp1[N], tmp2[N];
int qmi(int a, int k)
{
int res = 1;
while(k)
{
if(k & 1) res = res * a % p;
a = a * a % p;
k >>= 1;
}
return res;
}
int work1(int l, int r)
{
if (l > r) return 0;
return (s[l] - s[r + 1] + p) % p * qmi(qmi(2, n - L[r + 1] + 1), p - 2) % p;
}
int work2(int l, int r)
{
return (l > r) ? 0 : (tmp1[r] - tmp1[l - 1]);
}
int query(int l, int r, int x)
{
int idl, idr;
idl = upper_bound(L + 1, L + 1 + k, l) - L - 1, idr = upper_bound(L + 1, L + 1 + k, r) - L - 1;
if (idl == idr) return w[idl] * (qmi(2, x) - 1 + p) % p;
int b1 = 0, b4 = 0, s1, idz, sufz = tmp2[k - (idr + 1) + 1];
if (w[idl]) b1 = L[idl + 1] - l;
if (w[idr]) b4 = r - L[idr] + 1;
s1 = b1 + b4 + work2(idl + 1, idr - 1);
if (s1 >= x) return (qmi(2, x) - 1 + p) % p;
if (w[idr] == 0) sufz += L[idr + 1] - r - 1;
idz = lower_bound(tmp2 + 1, tmp2 + 1 + k, x - s1 + sufz) - tmp2;
idz = k - idz + 1;
b1 = b1 + work2(idl + 1, idz - 1);
return ((qmi(2, b1) - 1 + p) % p * qmi(2, x - b1) % p + work1(idz + 1, idr - 1) * qmi(2, r - L[idr] + 1) % p + qmi(2, b4) - 1 + p) % p;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m >> q;
for (int i = 1 ; i <= m ; i ++ )
{
int l, r;
cin >> l >> r;
c[2 * i - 1] = l;
c[2 * i] = r + 1;
}
sort(c + 1, c + 1 + 2 * m);
k ++ ;
for (int i = 1, cnt = 1, cv = 0; i <= 2 * m; i++)
{
cv ^= 1;
if ((c[i] != c[i + 1] || i == 2 * m) && c[i] <= n && cv != w[k])
{
k ++ ;
L[k] = c[i];
w[k] = cv;
}
}
if (k >= 2 && L[2] != 1) L[1] = 1;
L[k + 1] = n + 1;
for(int i = k ; i >= 1 ; i -- )
{
tmp2[i] = tmp2[i + 1];
s[i] = s[i + 1];
if (w[i]) s[i] = (s[i + 1] + (qmi(2, L[i + 1] - L[i]) - 1 + p) % p * qmi(2, n - L[i + 1] + 1) % p) % p;
else tmp2[i] += L[i + 1] - L[i];
}
reverse(tmp2 + 1, tmp2 + 1 + k);
for(int i = 1 ; i <= k ; i ++ )
{
tmp1[i] = tmp1[i - 1];
if (w[i])
tmp1[i] += L[i + 1] - L[i];
}
for (int i = 1, l, r, k1; i <= q; i++) cin >> l >> r >> k1, cout << query(l, r, k1) << endl;
return 0;
}
T6
P12029 [USACO25OPEN] Election Queries G
题目描述
农夫约翰有 \(N\) 头(\(2 \leq N \leq 2 \cdot 10^5\))编号从 \(1\) 到 \(N\) 的奶牛。农场正在举行选举,将选出两头新的领头牛。初始时,已知第 \(i\) 头奶牛会投票给第 \(a_i\) 头奶牛(\(1 \leq a_i \leq N\))。
选举过程如下:
- 农夫约翰任意选择一个非空真子集 \(S\)(即至少包含一头牛但不包含所有牛)。
- 在 \(S\) 集合中,得票数最多的候选牛将被选为第一头领头牛 \(x\)。
- 在剩余奶牛组成的集合中,得票数最多的候选牛将被选为第二头领头牛 \(y\)。
- 定义两头领头牛的差异度为 \(|x - y|\)。若无法选出两头不同的领头牛,则差异度为 \(0\)。
由于奶牛们经常改变主意,农夫约翰需要进行 \(Q\) 次(\(1 \leq Q \leq 10^5\))查询。每次查询会修改一头奶牛的投票对象,你需要回答当前状态下可能获得的最大差异度。
输入格式
第一行包含 \(N\) 和 \(Q\)。
第二行包含初始投票数组 \(a_1, a_2, \ldots, a_N\)。
接下来 \(Q\) 行,每行两个整数 \(i\) 和 \(x\),表示将 \(a_i\) 修改为 \(x\)。
输出格式
输出 \(Q\) 行,第 \(i\) 行表示前 \(i\) 次查询后的最大可能差异度。
输入输出样例 #1
输入 #1
5 3
1 2 3 4 5
3 4
1 2
5 2
输出 #1
4
3
2
输入输出样例 #2
输入 #2
8 5
8 1 4 2 5 4 2 3
7 4
8 4
4 1
5 8
8 4
输出 #2
4
4
4
7
7
说明/提示
样例一解释:
第一次查询后,\(a = [1,2,4,4,5]\)。选择 \(S = \{1,3\}\) 时:
- \(S\) 中:牛 \(1\) 得 \(1\) 票,牛 \(4\) 得 \(1\) 票 \(\to\) 可选择牛 \(1\) 或牛 \(4\) 作为第一头领头牛。
- 剩余牛中:牛 \(2,4,5\) 各得 \(1\) 票 \(\to\) 可选择牛 \(2,4,5\) 作为第二头领头牛。
最大差异度为 \(|1-5| = 4\)。
第二次查询后,\(a = [2,2,4,4,5]\)。选择 \(S = \{4,5\}\) 时:
- \(S\) 中:牛 \(4\) 得 \(1\) 票,牛 \(5\) 得 \(1\) 票。
- 剩余牛中:牛 \(2\) 得 \(2\) 票。
最大差异度为 \(|5-2| = 3\)。
- 测试点 \(3\sim4\):\(N,Q \leq 100\)。
- 测试点 \(5\sim7\):\(N,Q \leq 3000\)。
- 测试点 \(8\sim15\):无额外限制。
令奶牛 \(x\) 的得票数为 \(c_x\),记 \(mx=max{c_1...c_n}\) 。显然两头奶牛 x,y 能当选的充要条件为 \(mx \le c_x + c_y\)。考虑一种 \(O(n^2)\) 做法:对于每种 \(c\) 的值 \(v\),找出最小和最大的 \(i\) 满足 \(c_i = v\),枚举其中一个出现次数 \(c_x\) ,找出 \(c_x\) 对应的最小的 \(x_{min}\) ,使用双指针找出 \(c_y ≥mx−c_x\) 中的 \(y_max\) ,将所有情况取最大值即为答案。需要用到的值都可以用 set 维护。
构造 \(c_i = i\) 即可。由于 \(sum_{c_i} = n\),所以 \(c_i\) 的值只有本质不同的 \(O(\sqrt{n})\) 种。
于是对于上面的暴力做法,如果只考虑至少对应着一个 \(x\) 的 \(c_x\) ,时间复杂度就是 \(O(n\sqrt{n})\) 的。
#include <bits/stdc++.h>
using namespace std;
int n, q;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
vector<int> a(n), c(n);
for(auto &i : a)
{
cin >> i;
i -- ;
c[i] ++ ;
}
vector<set<int>> s(n + 1);
set<int> v;
for(int i : a) s[c[i]].insert(i), v.insert(c[i]);
while(q -- )
{
int p, x, r = 0;
cin >> p >> x;
p -- ;
x -- ;
s[c[a[p]]].erase(a[p]);
s[c[x]].erase(x);
if(s[c[a[p]]].size() == 0) v.erase(c[a[p]]);
if(s[c[x]].size() == 0) v.erase(c[x]);
c[a[p]] -- ;
s[c[a[p]]].insert(a[p]);
c[x] ++ ;
s[c[x]].insert(x);
v.insert(c[a[p]]), v.insert(c[x]), a[p] = x;
vector<int> e(v.begin(), v.end());
for (int i = 0, p = e.size() - 1, mx = 0 ; i < e.size() ; i ++ )
if(e[i])
{
while(p >= 0 && e[p] && e[p] + e[i] >= e.back())
{
mx = max(mx, *prev(s[e[p]].end()));
p -- ;
}
r = max(r, mx - *s[e[i]].begin());
}
cout << r << endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号