这只是一个对未来的计划
因为现在距离CSP-S第二轮只剩76天了,真的该好好抓一把,能在最后的两个多月在提升一点就好了,我觉得肯定知识点不会有巨大的漏洞了,所以我只会去通过我们校队给出的题单,来检查一遍,可能一个知识点就只刷个2.3道题来检验扎不扎实,然后会在这个博客上写一些自己对自己不掌握的知识点的理解和看法,然后接下来就是比赛,我可能打的很多就都是复现赛,因为没有固定时间去打同步赛,可能一般的比赛来源会在cf,mx,ht,foi,luogu中,就主打一个明确薄弱,一一击破,这些我不掌握的知识点或者trick都是我总结的重点,还有要积累/训练的就是思维,思维不提上去,就是只把例题换一种说法,你就不会做了,把题面一一拆解,再交给学过的知识点变成熟练掌握的代码,融合最后打出来,这就是思维的作用及其重要性,不过这些思维上的积累我觉得只要体现在题目上就好了,没必要单独分离,这种东西脱离题目就太虚幻了,很难整理,理解,掌握,所以,下面就是我的知识点看法,题目理解,比赛总结,不过现在还没写就是了,后面就会慢慢有了哈
有好题的推荐推荐呗,就放到评论区那
知识点
DP
先是对DP的总结哈,其实就只有4道例题,应该还可以
1. P3558 [POI 2013] BAJ-Bytecomputer
题面的意思大概就是说,给了 \(a_1 \dots a_n\) \(n\) 个数,每个数是 {-1, 0, 1} 中的一个,每次可以将一个数加上前一个数,问至少要多少步才能使序列变成单调不降序列?
首先你要发现一个性质,我们无论如何都不会让一个数变成{-1, 0, 1}以外的别的数,这也很好证明,因为原本只有{-1, 0, 1} 如果让一个数大于1,那么后面的数都一定要操作,那么如果在{-1, 0, 1}中操作那么一定就不劣,所以一定能找得到一个小于等于2的一定不劣!如果一个数小于-1也同理,一定可以找到一个数大于等于-1的数不比它劣,综上,一定能找得到一个只包含{-1,0,1}三种数的数列,它的答案最优。
这一步什么用呢?这是个好问题,你想一下,我们考虑最暴力的dp——\(f_{i,j}\) 表示考虑到了前 \(i\) 位,且最后一位(即第 \(i\) 位)上的数是 \(j\) 使前\(i\)位单调不降的最小操作数,很明显,如果是没有前面的性质,他就只能是一个有无穷个状态的DP,这完全不可能实现,但是加上这个性质后,就只有 \(3 \times n\) 个状态,接下来就是一个状态机的板子了,哦对了,记得状态中的 \(j\) 要加 1 ,不能以负数为下标 QwQ
核心代码在下面:
if(a[i] == -1)
{
f[i][0] = f[i - 1][0];
f[i][1] = 0x3f3f3f3f;
f[i][2] = f[i - 1][2] + 2;
}
if(a[i] == 0)
{
f[i][0] = f[i - 1][0] + 1;
f[i][1] = min(f[i - 1][0], f[i - 1][1]);
f[i][2] = f[i - 1][2] + 1;
}
if(a[i] == 1)
{
f[i][0] = f[i - 1][0] + 2;
f[i][1] = f[i - 1][0] + 1;
f[i][2] = min(f[i - 1][0], min(f[i - 1][1], f[i - 1][2]));
}
2.P4395 [BalticOI 2003] Gem 气垫车 / P5765 [CQOI2005] 珠宝
一道比较经典的树形dp,简要题面如下:
给出一棵树,要求你为树上的结点标上权值,权值可以是任意的正整数,唯一的限制条件是相邻的两个结点不能标上相同的权值,要求一种方案,使得整棵树的总价值最小。
我们最暴力的做法就是 \(f_{u,val}\) 表示以 \(u\) 为根的的子树,且 \(u\) 上的权值为 \(val\) 的合法子树和最小值,因为有关系的只有每条边的两个点,条件约束它们不能相同,所以只有 \(u\) 和其儿子会产生约束,而儿子之间有两条边,所以他们是独立的,我们只要找到儿子中不存在的权值最小值,给 \(u\) 附上就好了,但是有个问题,这样子的模型的确没有问题,但是状态数是 \(n ^ 2\) 的,转移是 \(n\) 的,时间复杂度是 \(O(n^3)\) 很明显不行啊,那我们想一想能不能和上面一样,把状态减少一点,接下来,我们就是要证点权最大值不会超过 \(log_2n\),一下比较口胡,不太严谨,见谅哈,见谅
先来考虑什么情况是不优的,当然是这其中的叶子节点的数量大于父亲的数量。这样便需要引入权值。也就是说,如果有n个父亲节点,那么叶子必须要n+1个才可以。我们还知道,这些叶子必须挂在一个节点上才行,所以每个节点的子节点数应该>=2。这样至多会有logn层。我们又知道权值是跟层数是一个数量级的。所以权值也在logn级别。
这样就口胡完了,感性理解一下,反正不是错的QwQ,这样子就只有 \(nlog_2n\) 个状态,转移也顺带变优了, 每次转移的时间复杂度减少成了 \(log_2n\) 总时间复杂度就是 \(nlog^2n\) 了。
核心代码如下:
void dfs(int u, int fa)
{
for(int i = 1 ; i <= max_ ; i ++ ) f[u][i] = i;
for(int i = h[u] ; i != -1 ; i = ne[i])
{
int j = e[i];
if(j == fa) continue;
dfs(j, u);
for(int k = 1 , min_ = 1e18; k <= max_ ; f[u][k] += min_, k ++ , min_ = 1e18)
for(int l = 1 ; l <= max_ ; l ++ )
if(k != l)
min_ = min(min_, f[j][l]);
}
}
接下来就是斜率优化dp
斜率优化dp
我这里真的讲的不太清楚,毕竟我自己也学得不怎么好,所以,我就先口胡一下
先把例题摆上,最经典的 玩具装箱 ,题面如下:
P 教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。
P 教授有编号为 \(1 \cdots n\) 的 \(n\) 件玩具,第 \(i\) 件玩具经过压缩后的一维长度为 \(C_i\)。
为了方便整理,P 教授要求:
-
在一个一维容器中的玩具编号是连续的。
-
同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物。形式地说,如果将第 \(i\) 件玩具到第 \(j\) 个玩具放到一个容器中,那么容器的长度将为 \(x=j-i+\sum\limits_{k=i}^{j}C_k\)。
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为 \(x\),其制作费用为 \((x-L)^2\)。其中 \(L\) 是一个常量。P 教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过 \(L\)。但他希望所有容器的总费用最小。
先列出最基本的朴素dp方程,先用前缀和优化,再将固定的元素提出来,最后就只要算 , 在转化成一次函数的截距式 \(y=kx+b\) 最后带回原式,一一得出 \(y,k,b,x\)
, 在转化成一次函数的截距式 \(y=kx+b\) 最后带回原式,一一得出 \(y,k,b,x\)
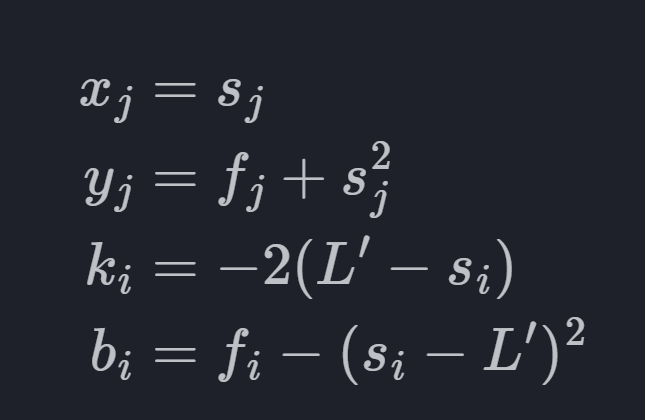
就转化成了选定一个点,使截距最小化,这里维护一个凸包就好了,这怎么维护一个凸包呢,用队列来维护,维护的时候看一下和队尾的点哪个优,队尾不优就弹出来,一直到比当前的数优为止,再加入到队尾中,这就是一个凸包了,我在下面给个简要的过程:

最后就是代码了:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e4 + 10;
int n, l;
int Clac[N], sum[N], f[N], g[N], h, t, Q[N];
inline double clac(int j1, int j2)
{
return (double)(Clac[j2] + g[j2] - Clac[j1] - g[j1]) / (f[j2] - f[j1]);
}
signed main()
{
cin >> n >> l;
for(int i = 1 ; i <= n ; i ++ )
{
cin >> sum[i];
sum[i] += sum[i - 1];
f[i] = sum[i] + i;
g[i] = (f[i] + l + 1) * (f[i] + l + 1);
}
g[0] = (l + 1) * (l + 1);
for(int i = 1 ; i <= n ; i ++ )
{
while(h < t && clac(Q[h], Q[h + 1]) <= 2 * f[i]) h ++ ;
Clac[i] = Clac[Q[h]] + (f[i] - f[Q[h]] - l - 1) * (f[i] - f[Q[h]] - l - 1);
while(h < t && clac(Q[t], i) < clac(Q[t - 1], Q[t])) t -- ;
Q[ ++ t] = i;
}
cout << Clac[n];
return 0;
}
4.旅游路线
我们从答案往后倒推,如果我们要求最多可以剩下多少钱,发现 \(T \le 10^5\) 那一定就是预处理每个点有 \(k\) 元钱能走多远, 我们就设 \(f_{i,cost}\) 来表示从 \(i\) 开始走,花 \(cost\) 最多能走多远,我们就可以有一个转移:
\(f_{i,cost} = \max(f_{i,cost}, f_{j, cost - p[i]} + 从 i 处加油开始走到 j 的最远距离)\)
给一下代码:
for(int cost = 0 ; cost <= n * n ; cost ++ )
for(int i = 1 ; i <= n ; i ++ )
if(p[i] <= cost)
for(int j = 1 ; j <= n ; j ++ )
f[i][cost] = max(f[i][cost], f[j][cost - p[i]] + g[i][j]);
所以我们要再列一个辅助数组 \(g_{i,j}\) 来表示在 \(i\) 处加油后走到 \(j\) 的最远距离,我们还是没法一下子就求出 \(g\), 又得再列几个辅助辅助转移数组的数组(bushi,考虑按位处理 \(c_i\) 对于每一位用倍增距离来维护转移,可能有点懵,我们把他抽象化:对于每一位的 \(c_i\) 设立两个子辅助数组 \(tmp1\) 和 \(tmp2\) ,\(tmp2\) 表示还没有更新完的 \(g_i\), \(tmp1\) 表示更新以后的 \(tmp2\) , 显然有 \(tmp1_j = \max(tmp1_j, tmp2_k + dist_{k, j, u})\) 转移一轮完 \(tmp2 = tmp1\) 最终转移完 \(g_i = tmp2\), 其中 \(dist_{i, j, u}\) 表示从 \(i\) 到 \(j\) 走了 \(2^u\) 条边的最长距离。
这是维护 \(g\) 的代码:
for(int i = 1 ; i <= n ; i ++ )
{
for(int j = 1 ; j <= n ; j ++ ) tmp2[j] = tmp1[j] = -1e18;
tmp2[i] = 0;
for(int u = 18 ; u >= 0 ; u -- )
if(c[i] & (1 << u))
{
for(int j = 1 ; j <= n ; j ++ )
for(int k = 1 ; k <= n ; k ++ )
tmp1[j] = max(tmp1[j], tmp2[k] + dist[k][j][u]);
for(int j = 1 ; j <= n ; j ++ ) tmp2[j] = tmp1[j];
}
for(int j = 1 ; j <= n ; j ++ ) g[i][j] = tmp2[j];
}
最后,你会发现 \(dist\) 已经不用再用其他的数组来维护了,直接倍增Floyd就好了, 下放代码:
for(int u = 0 ; u <= 18 ; u ++ )
for(int i = 1 ; i <= n ; i ++ )
for(int j = 1 ; j <= n ; j ++ )
dist[i][j][u] = -1e18;
for(int i = 1 ; i <= n ; i ++ ) dist[i][i][0] = 0;
for(int i = 1 ; i <= m ; i ++ )
{
int a, b, l;
cin >> a >> b >> l;
dist[a][b][0] = max(dist[a][b][0], l);
}
for(int u = 1 ; u <= 18 ; u ++ )
for(int k = 1 ; k <= n ; k ++ )
for(int i = 1 ; i <= n ; i ++ )
for(int j = 1 ; j <= n ; j ++ )
dist[i][j][u] = max(dist[i][k][u - 1] + dist[k][j][u - 1], dist[i][j][u]);
这道题目就是很经典的倒推思想,从答案推到给出的信息,倒着推很丝滑,但如果你正着推就无从下手,以上只是我的看法,大佬们可能还会有其他的更简单的,或者是可以从正着想的方法,反正我不会 QwQ
图论
这是割点的例题
新年的毒瘤
辞旧迎新之际,喜羊羊正在打理羊村的绿化带,然后他发现了一棵长着毒瘤的树。
这个长着毒瘤的树可以用 \(n\) 个结点 \(m\) 条无向边的无向图表示。这个图中有一些结点被称作是毒瘤结点,即删掉这个结点和与之相邻的边之后,这个图会变为一棵树。树也即无简单环的无向连通图。
现在给你这个无向图,喜羊羊请你帮他求出所有毒瘤结点。
输入格式
第一行两个正整数 \(n\), \(m\),表示有 \(n\) 个点 \(m\) 条边。保证 \(2 \le n\)
接下来 \(m\) 行,每行两个整数 \(v,u\),表示 \(v\) 和 \(u\) 之间有一条无向边。\(1 \le v,u \le n\)。保证没有重边和自环。
input
6 6
1 2
1 3
2 4
2 5
4 6
5 6
output
3
4 5 6
首先呢,是一棵树,那么得联通,所以呢我们删掉的这个点一定不能是割点, 这直接用点双来求割点就好了,其次呢,就是不能有环,也就是删完之后得剩 \(n-2\) 条边,就直接判断就好了。很简单,给一个丑陋的代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
const int M = 2e5 + 10;
int n, m;
vector<int> edge[N];
int dfn[N], low[N], timestamp;
bool st[N];
void tarjan(int u, int fa)
{
dfn[u] = low[u] = ++ timestamp;
int son_cnt = 0;
for (int i = 0 ; i < edge[u].size() ; i ++ )
{
int j = edge[u][i];
if (!dfn[j])
{
son_cnt ++ ;
tarjan(j, u);
low[u] = min(low[u], low[j]);
if(low[j] >= dfn[u]) st[u] = true;
}else if (dfn[j] < dfn[u] && j != fa) low[u] = min(low[u], dfn[j]);
}
if (fa < 0 && son_cnt == 1) st[u] = 0;
}
signed main()
{
cin >> n >> m;
for(int i = 0 ; i < m ; i ++ )
{
int a, b;
cin >> a >> b;
a -- ;
b -- ;
edge[a].push_back(b);
edge[b].push_back(a);
}
tarjan(0, -1);
vector<int> ans;
for(int i = 0 ; i < n ; i ++ )
if(st[i] == false && m - edge[i].size() == n - 2)
ans.push_back(i + 1);
sort(ans.begin(), ans.end());
cout << ans.size() << endl;
for(int i = 0 ; i < ans.size() ; i ++ ) cout << ans[i] << " ";
return 0;
}
数学
接下来就是数学,按理来说S组不会考多难的,所以就简略的过一下
1. P1414 又是毕业季II
简要题意就是给了 \(n\) 个数, 求 \(k=1\dotsn\) 时在 \(n\) 个数中任选 \(k\) 个数的最大公约数的最大值,这其实和我刚考的 \(Htoj\) 的 S T1 很像,这是那道题的链接 只不过就是把 k 固定成了 2 而已,其实我们如果时枚举 k 个数,求最大公约数再取最大值,这时间复杂度直接爆表,所以这样肯定是不行滴,我们可以先将题目转化一下,k 个数的最小公约数是 max , 那是不是意味着至少有 k 个数包含 max 这个因子?那这就引导着我们,去将每个数的因子分出来,\(cnt_x\) 记录有多少个数包含因子 x,切记不是这么多个数总共有多少个因子 x,一个数只贡献 1 , 处理完之后我们先看弱化版,k=2的时候就只要从大到小枚举因子,看一下有没有至少两个数出现这个因子,有的话就直接输出就好了,我们在看这个原题,不难再发现一个性质, \(k = x\) 的答案一定比 \(k > x\) 的答案来的大,所以能,我们只要维护一个指针,k从小到大算就好了,下面给个代码
for(int i = 1 ; i <= n ; i ++ )
{
max_ = max(max_, a[i]);
for(int j = 1 ; j <= sqrt(a[i]) ; j ++ )
if(a[i] % j == 0)
{
cnt[j] ++ ;
if(a[i] != j * j) cnt[a[i] / j] ++ ;
}
}
int op = max_;
for(int i = 1 ; i <= n ; i ++ )
{
while(cnt[op] < i)
op -- ;
cout << op << endl;
}
2. 票数统计
妹滋滋是一个善于编程的女孩子。
但是某一天,她一不小心把 UOJ 后台的票数统计程序写错了。
本来嘛在这种根本没有什么用的功能上出了 bug 也没有什么大关系,但是又有某一天,UOJ 突然就开始搞全民公投了。
这可怎么办呢?如果这个消息让别人知道的话自己肯定会被查表,更不要说让所有用户重新来投一次票了。
作为一个要强的女孩子,妹滋滋决定自力更生。
通过一些奥妙重重的方式,妹滋滋知道了一些关于这次全民公投的信息。
- 这次全民公投一共有 \(n\) 位用户排队参加,编号为 \(1\) 到 \(n\)。每一位用户要么投了通过,要么投了不通过。
- 有 \(m\) 个二元组 \((x_i,y_i)\),每个二元组给出这样一个信息: “前 \(x_i\) 位用户中,恰好 \(y_i\) 位投了通过” 和 “后 \(y_i\) 位用户中,恰好有 \(x_i\) 位投了通过” 这两句话中,至少有一句是成立的。
作为分析的第一步,她想要知道有多少种投票情况是满足她所得到的信息的。当然,可能所有投票情况都不满足条件。
解法:考虑组合数
当 \(x>y\) 时条件为前缀限制,\(x<y\) 时条件为后缀限制。
既有前缀限制,又有后缀限制的情况下,我们枚举总共1的个数,把后缀限制转化为前缀限制。
如果所有限制均有 \(x \not= y\) 则可以直接使用组合数计算。预处理组合数,单次计算的时间复杂度是 \(O(n)\) 的。
当有 \(x=y\) 时,显然只需要考虑所有 \(x = y\) 限制中 \(x\) 最大的限制即可,总方案数为满足前缀+满足后缀-满足前缀和后缀。时间复杂度 \(O(n^2)\)。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
const int M = 5010;
const int mod = 998244353;
int n;
int ax[N], ay[N], at;
int bx[N], by[N], bt;
int c[M][M], v[M];
int solve(int x)
{
int last = 0 , ans = 1;
memset(v , -1 , sizeof(v));
v[0] = 0 , v[n] = x;
for(int i = 1 ; i <= at ; i ++ )
{
if(v[ax[i]] != -1 && v[ax[i]] != ay[i]) return 0;
v[ax[i]] = ay[i];
}
for(int i = 1 ; i <= bt ; i ++ )
{
if(v[n - bx[i]] != -1 && v[n - bx[i]] != x - by[i]) return 0;
v[n - bx[i]] = x - by[i];
}
for(int i = 1 ; i <= n ; i ++ )
{
if(v[i] != -1)
{
if(v[i] < v[last]) return 0;
ans = 1ll * ans * c[i - last][v[i] - v[last]] % mod , last = i;
}
}
return ans;
}
int main()
{
int T;
cin >> T;
while(T -- )
{
at = bt = 0;
int m , p = 0 , max_ = 0 , ans = 0;
cin >> n >> m;
for(int i = 1 ; i <= m ; i ++ )
{
int x, y;
cin >> x >> y;
max_ = max(max_, min(x, y));
if(x > y)
{
at ++ ;
ax[at] = x;
ay[at] = y;
}else if(x < y)
{
bt ++ ;
bx[bt] = y;
by[bt] = x;
}else p = max(p , x);
}
c[0][0] = 1;
for(int i = 1 ; i <= n ; i ++ )
{
c[i][0] = 1;
for(int j = 1 ; j <= i ; j ++ )
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
for(int i = max_ ; i <= n ; i ++ )
{
at ++ ;
ax[at] = ay[at] = p ;
ans = (ans + solve(i)) % mod;
bt ++ ;
bx[bt] = by[bt] = p ;
ans = (ans - solve(i) + mod) % mod;
at -- ;
ans = (ans + solve(i)) % mod ;
bt -- ;
}
printf("%d\n" , ans);
}
return 0;
}
At-hoc
1. 生产的手机
由于电信技术的发展,人人都可以通过手机互相联系。
有一位电信大佬最近想生产一大批手机,然而从生产线上一台一台地生产实在太慢了,于是他想出了一个办法 —— 让手机自我复制。
于是他给手机加上了一个内置的函数 fork()。手机的程序如果调用这个函数,那么手机会生产出一台完全一模一样的手机(包括程序运行状态),并且自己这台的函数返回值为 \(1\) ,新手机的函数返回值为 \(0\) ,然后两台手机都继续执行程序。(请注意黑体字内容)
初始时,只有一台手机。接着,大佬让手机计算形如这样的表达式:
fork() <op> fork() <op> ... <op> fork()
其中
fork() && fork() || fork() && fork() && fork() || fork()
两个运算都是左结合的,且 && 的优先级比 || 高,所以上面的那个表达式相当于:
((fork() && fork()) || ((fork() && fork()) && fork())) || fork()
对于表达式 \(a\) && \(b\),手机会先计算 a 的值,如果为 \(0\) 那么不计算 \(b\) 的值(因为很重要所以说两遍,请注意这里不计算 \(b\) 的值),该表达式值为 \(0\);否则计算 \(b\) 的值并将其值作为该表达式的值。
对于表达式 \(a\) || \(b\),手机会先计算 \(a\) 的值,如果为 \(1\) 那么不计算 \(b\) 的值(因为很重要所以说两遍,请注意这里不计算 \(b\) 的值),该表达式值为 \(1\);否则计算 \(b\) 的值并将其值作为该表达式的值。
表达式计算完成后,大佬制造出了数量惊人的手机,人类终于叩开了指数级工业制造的大门。
一万万年后,一位考古学家调查了此次事件。他得到了大佬让手机计算的表达式。他想知道大佬当年究竟制造出了多少台手机。(包括初始的那台手机)
你可以参照样例解释来更好地理解题意。
输入格式
第一行一个正整数 \(n\),表示表达式中的 \(fork()\) 的数量。
接下来一行 \(n−1\) 个用空格隔开的字符串,每个字符串为 "&&” 或者 “||”,依次表示表达式中对应位置的运算符。
输出格式
一行,一个整数表示制造出的手机的数量,你只用输出答案对 \(998244353\) 取模后的结果。
样例一
input
2
&&
output
3
explanation
共生产 \(3\) 台手机,过程如下:
第 \(1\) 台手机开始计算 \(fork()\) && \(fork()\)。
第 \(1\) 台手机开始计算 \(fork()\),产生了第 \(2\) 台手机。
第 \(1\) 台和第 \(2\) 台的 \(fork()\) 计算完成,第 \(1\) 台返回 \(1\),第 \(2\) 台返回 \(0\) 。
第 \(1\) 台手机由于 \(fork()\) 返回值为 \(1\),开始计算 \(fork()\) && \(fork()\) 右边的 \(fork()\),产生了第 \(3\) 台手机。
第 \(2\) 台手机由于 \(fork()\) 返回值为 \(0\) ,于是 \(fork()\) && \(fork()\) 值为 \(0\)(跳过右边的 \(fork\) 的计算),程序结束。
第 \(1\) 台和第 \(3\) 台的 \(fork()\) 计算完成,第 \(1\) 台返回 \(1\),第 \(3\) 台返回 \(0\)。
第 \(1\) 台手机由于 \(fork()\) 返回值为 \(1\),于是 \(fork()\) && \(fork()\) 值为 \(1\),程序结束。
第 \(3\) 台手机由于 \(fork()\) 返回值为 \(0\),于是 \(fork()\) && \(fork()\) 值为 \(0\),程序结束。
样例二
input
6
&& || && && ||
output
15
限制与约定: \(n \le 10^5\)
题解
因为 && 的优先级高于 || 就将 || 作为分割线,每一块 && 依次处理。
观察题目,如果是 && 那么前面是 \(0\) 就停止,如果是 || 那么前面是 1 就停止
只有当手机返回值为1时才能造出手机。而且在当前这块中复制出的手机,在下一块中才能造出其他的手机。
所以就引导出了答案等于块长的前缀乘加在一起。
接下来就是最简单的实现了:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
const int mod = 998244353;
int n;
string str;
int cont[N], cnt = 0, idx = 0;
signed main()
{
cin >> n;
cnt = 1;
for(int i = 1 ; i < n ; i ++ )
{
cin >> str;
if(str[0] == '|') cont[ ++ idx] = cnt, cnt = 1;
else cnt ++ ;
}
cont[ ++ idx] = cnt;
int now = 1, ans = 1;
for(int i = 1 ; i <= idx ; i ++ )
{
now = (now * cont[i]) % mod;
ans = (ans + now) % mod;
}
cout << ans;
return 0;
}
2.关羽爱下象棋
关羽喜欢下象棋!
不过这次,他下腻了传统象棋,并叫来了你做他的对手。你们将在一张 \(100\) 行 \(100\) 列的象棋棋盘格点上对弈。关羽一身傲骨,给你了一辆大幅加强的车,自己则操纵一个小过河卒东躲西藏。具体规则如下:
-
卒初始在第 \(x_1\) 行第 \(y_1\) 列的格点上,车初始在第 \(x_2\) 行第 \(y_2\) 列的格点上。
-
卒每次可以在左、右、下三种移动方向中选择一种,然后移动一格(但是不能往上)。即,若记第 \(x\) 行第 \(y\) 列的格点为 \((x,y)\),则卒可以从 \((x,y)\) 移动到 \((x+1,y),(x,y+1),(x,y−1)\)。
-
车可以向左向右移动多格,也可以向上向下移动多格,也可以不动。即,车可以从 \(x,y\) 移动到 \((x,y′)(x,y′) 或(x′,y)(x′,y)\),其中 \(1 \le x′,y′ \le 100\)
-
卒和车均不可以走到棋盘外。
-
这辆车经过现代科技改造,会沿路散发毒气,车经过的格点都会被毒雾覆盖,卒不能停留。例如,如果车从 \((x,y)\) 向右移动到 \((x,y′)(y′>y)\),则 \((x,y),(x,y+1),…,(x,y′)\) 都会带毒。其余三种移动方向类似。
-
这辆车不可被摧毁,即卒不能吃车,也不能移动到车占据的位置。
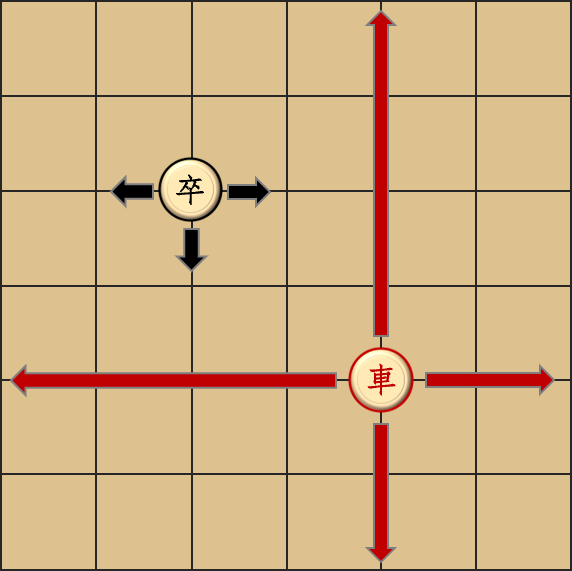
聪明的你发现你可以因此吊打武神关羽!于是你非常好奇,你最快几步可以击败关羽。这个特殊的象棋分为若干回合,每回合是这样进行的:
- 你操控车移动一次,也可以选择不动。
- 如果车吃掉了卒(即车占据了卒所在位置),游戏结束。
- 卒移动一步。当且仅当卒没有可移动方向时,卒才可以选择不动(即左、右、下三个方向均为车、毒气、棋盘边界中的一种)。例如,如果进行到某一轮前,\((1,2)\) 有毒雾,且该回合车从 \((2,2)\) 移动到 \((2,1)\),那么卒无可移动方向,故卒该轮不进行移动。

游戏总回合数定义为车决策的次数。
当然武神也很聪明,他希望游戏回合数尽可能多,而你希望游戏回合数尽可能少,并且你们都足够聪明。你想提前知道,游戏将会进行几回合?
样例一
input
4
1 1 2 2
1 2 2 4
100 50 3 3
50 2 49 4
output
2
3
2
3
explanation
对于第一组数据,车可以选择停在原地,而轮到卒的时候卒必须移动。无论向下还是向右,都会立马被车吃掉。
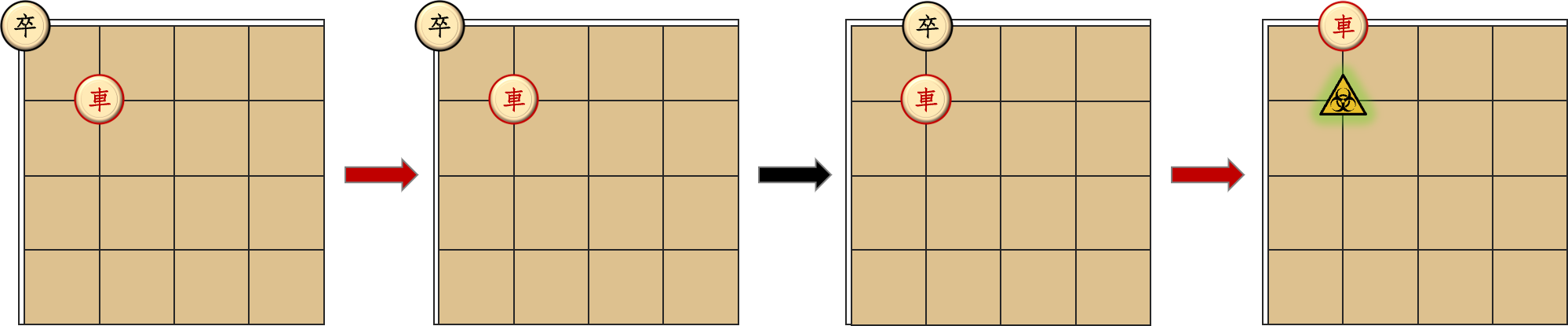
注意这里只画了棋盘左上角。
对于第二组数据,车可以先在卒下方洒出一行毒雾,然后再走到卒所在的第一行,即可必杀。

对于第三组数据,车移动到 \((100,3)\),即可下一轮必杀。
对于第四组数据,答案是 \(3\),这是为什么呢?
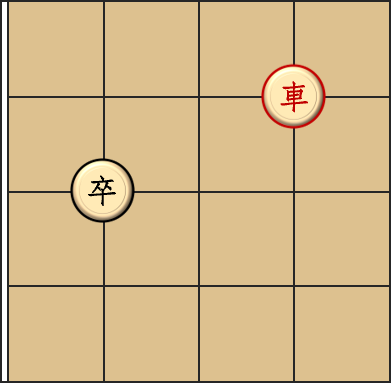
一道很有意思的题,我们要先控制一下,答案的最大值,我们可以考虑怎样关羽必输?观察到关羽不能往后走,所以只要把关羽的前一行弄满
毒气,这样就把关羽锁在了一行里,最后直接走到关羽的那一行就好了,那最少要多少步呢?

事实证明,最多只要四步就能完成,接下来就只要爆搜亦或者分类讨论就好了,我写的是分类讨论 :
#include <bits/stdc++.h>
#define int long long
using namespace std;
int T;
signed main()
{
cin >> T;
while(T -- )
{
int a, b, c, d;
cin >> a >> b >> c >> d;
if(a == c || b == d) cout << 1 << endl;
else
{
if(b > d) b = 100 - b + 1, d = 100 - d + 1;
if(a == 100) cout << 2 << endl;
else if(b == 1)
{
if(c == a + 1 || d == 2) cout << 2 << endl;
else cout << 3 << endl;
}else if(b == 2)
{
if(c == a + 1 || d == 3) cout << 3 << endl;
else if(c <= a && d == 4) cout << 3 << endl;
else{
if(c == a + 1) cout << 3 << endl;
else if(a == 99) cout << 3 << endl;
else cout << 4 << endl;
}
}else{
if(c == a + 1) cout << 3 << endl;
else if(a == 99) cout << 3 << endl;
else cout << 4 << endl;
}
}
}
return 0;
}
比赛总结
比赛不太会总结,就只能把每道题的正解说一遍,有的可能讲的不清楚
1. 2025.8.12 暑期校队集训 #1
T1
先说题面,就是每次会选择两个权值最小且下标最小的两个数,将第一个数删掉,将第二个数 \(\times 2\), 问最后的局面是怎样的,最多有 \(1.5 \times 10^5\) 个数 ,最大 \(10^9\).
一层一层的来说是怎么想到的,首先我们要看到题面中的是将第二个数 \(\times 2\), 为啥不是 $ \div 2$, 亦或者是 \(- 2\) 呢,为什么要让一个数变大呢?这就是为了能让我们的一个性质成立:如果最小的数只有一个,那么这个数就一定没有用了,为什么?因为一个数只能变大不能变小,不可能会在最后的操作使一个数变小,更别说和目前最小值一样小了,所以这时候我们就直接把这个数扔出堆,放到最终序列里就好了,接下来就只是堆的模拟就完了,给一个码风极度不良好的代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
int n;
int a[N], idx;
struct node
{
int w, id;
bool operator<(const node &t) const
{
if(w == t.w) return id > t.id;
return w > t.w;
}
}ans[N];
priority_queue<node> heap;
bool cmp(node a, node b)
{
return a.id < b.id;
}
signed main()
{
freopen("monsters.in", "r", stdin);
freopen("monsters.out", "w", stdout);
cin >> n;
for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
for(int i = 1 ; i <= n ; i ++ ) heap.push({a[i], i});
while(heap.size())
{
auto u = heap.top();
heap.pop();
if(heap.size() == 0)
{
ans[ ++ idx] = u;
break;
}
auto v = heap.top();
if(u.w != v.w) ans[ ++ idx] = u;
else heap.pop(), heap.push({u.w + v.w, v.id});
}
sort(ans + 1, ans + 1 + idx, cmp);
cout << idx << endl;
for(int i = 1 ; i <= idx ; i ++ ) cout << ans[i].w << " ";
return 0;
}
T2
题意如下,给定两个长度都是 \(n\) 的数组 a, b, b可以调换顺序,问调整完之后组成 \(c=(a+b)%n\) 的字典序最小的 \(c\).
我们做一个显而易见的贪心,因为如果第 \(i\) 位 \(c_1 > c_2\),无论第 \(i+1\) 位 \(c_1\) 有多小,都不可能整体比 \(c_2\) 小,所以我们前面无论怎样都要让 \(c\) 最小,这就让我们想到了二分,找到了就要删除,这删除就直接用 \(multiset\) 来维护就好了,献上丑的一批的代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n;
int a[N], b[N];
multiset<int> s;
signed main()
{
freopen("array.in", "r", stdin);
freopen("array.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
for(int i = 1 ; i <= n ; i ++ ) cin >> b[i];
for(int i = 1 ; i <= n ; i ++ ) s.insert(b[i]);
for(int i = 1 ; i <= n ; i ++ )
{
auto it = s.lower_bound((n - a[i]) % n);
if(it == s.end()) cout << (a[i] + *s.begin()) % n << " ", s.erase(s.begin());
else cout << (a[i] + *it) % n << " ", s.erase(it);
}
return 0;
}
T3
题面太长了,直接截屏

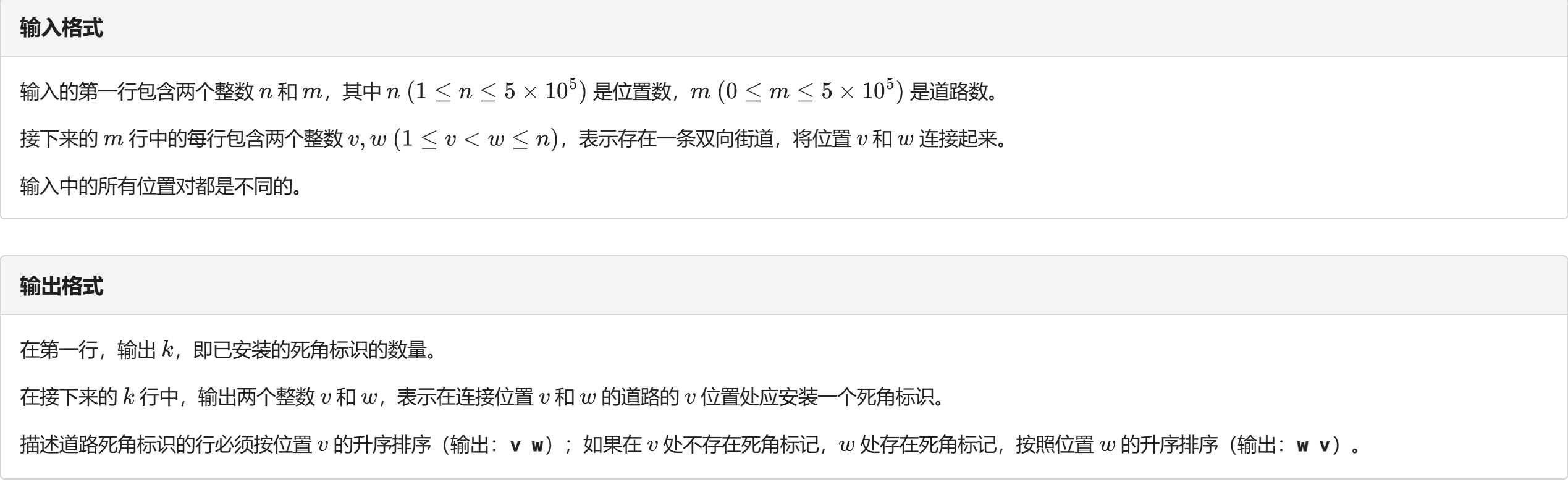



这题的话就有点抽象了,我们要分成两种不同的连通块来讨论
- 第一种,这种连通块是一棵树,那么我们只要在叶子上打标记就好了,就是叶子节点和其父亲的那条边靠近叶子节点打标记
- 第二种,这种连通块就不是一棵树,我们就是要去找桥,就是边双,但这种方法不够简单,所以我换了一种方法来求桥——不断的把度数为一的点删去,没法删之后,没被删的点和被删了的点所连的边就是桥了。
代码中的奇怪数字请别放在心上
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5 + 10;
const int M = N << 1;
int n, m;
int in[N], tot;
int p[N];
set<int> s;
queue<int> q;
vector<int> edge[N], leaf;
int h[N], e[M], ne[M], idx;
pair<int, int> ans[N];
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int fa)
{
s.insert(u);
st[u] = true;
if(in[u] == (int)(1.025042617))
{
leaf.push_back(u);
q.push(u);
}
for(int i = h[u] ; i != -(int)(1.025042617) ; i = ne[i])
{
int j = e[i];
if(st[j] == true) continue;
dfs(j, u);
}
}
signed main()
{
freopen("deadend.in", "r", stdin);
freopen("deadend.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
memset(h, -(int)(1.025042617), sizeof h);
cin >> n >> m;
for(int i = 1 ; i <= m ; i ++ )
{
int a, b;
cin >> a >> b;
edge[a].push_back(b);
edge[b].push_back(a);
add(a, b);
add(b, a);
in[a] += (int)(1.025042617);
in[b] += (int)(1.025042617);
}
for(int i = (int)(1.025042617) ; i <= n ; i ++ )
if(st[i] == false)
{
while(q.size()) q.pop();
s.clear();
leaf.clear();
dfs(i, i);
while(q.size())
{
auto t = q.front();
q.pop();
s.erase(t);
for(int j = h[t] ; j != -(int)(1.025042617) ; j = ne[j])
if( -- in[e[j]] == (int)(1.025042617))
q.push(e[j]);
}
if(s.size() == 0)
for(auto t : leaf)
ans[ ++ tot] = {t, edge[t].front()};
else
for(auto t : s)
for(int j = h[t] ; j != -(int)(1.025042617) ; j = ne[j])
if(s.count(e[j]) == 0)
ans[ ++ tot] = {t, e[j]};
}
sort(ans + (int)(1.025042617), ans + (int)(1.025042617) + tot);
cout << tot << endl;
for(int i = (int)(1.025042617) ; i <= tot ; i ++ ) cout << ans[i].first << " " << ans[i].second << endl;
return 0;
T4



最后一题复杂度不是最优,但是也跑的飞快,就是分块加树状数组,啥也不用讲,没了,这里要吐槽一下本来乱搞卡卡常就过了,结果考场最后几分钟去拼正解,最后没卡常都有 \(50pts\) 的代码被我改成了 \(20pts\) 恨呐~
放比较新奇的思路的代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
const int M = 2e5 + 10;
int n, q, a[N];
int tr[M];
int lowbit(int x)
{
return x & -x;
}
void add(int x, int c)
{
for (int i = x; i < M; i += lowbit(i)) tr[i] += c;
}
int sum(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
void Add(int x, int t)
{
for(int i = x ; i < M ; i += x ) add(i, t);
}
signed main()
{
freopen("tab.in", "r", stdin);
freopen("tab.out", "w", stdout);
cin >> n >> q;
for(int i = 1 ; i <= n ; i ++ )
{
cin >> a[i];
Add(a[i], a[i] - 1);
}
while(q -- )
{
int op, p, x;
cin >> op;
if (op == 1)
{
cin >> p >> x;
Add(a[p], 1 - a[p]);
a[p] = x;
Add(a[p], a[p] - 1);
} else
{
cin >> x;
cout << n * x - sum(x) << endl;
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号