树的直径

证明

求树的直径的方法：

1. 选择树上任意一点，从该点dfs，求其它所有点到x的距离distx[]
2. 从distx[]中选择一个最大的距离所对应的点y，从y开始再次dfs求一个disty[]
3. disty[]中的最大值就是树的直径

求树的直径的bfs/dfs方法的正确性证明：

问题就在第一点：距离x最远的y点在树的直径上。

现在证明这个结论

反正法：

假设y不在直径上，那么有以下情况：

1. 树的直径和\(x -> y\)的路径存在交点。
   

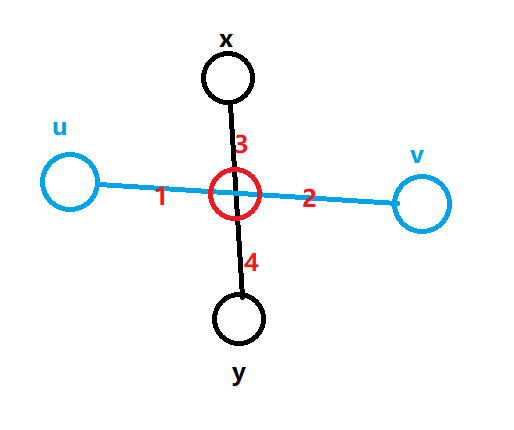
​ 此时\(u -> v\)为树的直径

​ 而\(dist(x, y) \ge dist(x, u)\)它们存在公共部分\(3\), 所以有\(1 \le 4\)

​ 从而\(1 + 2 \le 4 + 2\), 所以有\(dist(u, v) \le dist(y, v)\)

​ 那么\(dist(y, v)\)就成了直径，\(y\)成了直径的端点，与假设矛盾。

2. 树的直径和\(x -> y\)的路径不存在交点。
   

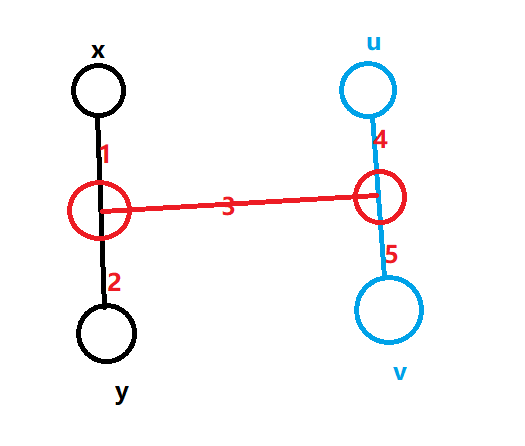
​ 此时\(u -> v\)

为树的直径

​ 因为\(dist(x, y) \ge dist(x, v)\)

​ 所以有\(1 + 3 + 5 \le 1 + 2\)

​ \(\to 3 + 5 \le 2\)

​ \(\to 2 + 3 \ge 5\)

​ \(\to 2 + 3 + 4 \ge 5 + 4\)

​ \(\to dist(y, u) \ge dist(u, v)\)

​ 所以\(dist(y, u)\)为树的直径，所以\(y\)为树的直径上的端点，与假设矛盾。

综上，结论“距离x最远的y点在树的直径上”结论获证。

代码

#include<iostream>
#include<cstring>

using namespace std;

const int N = 100010, M = 200010;

int h[N], e[M], ne[M], w[M], idx;
int n;
int dist[N], st[N];

int add(int a, int b, int c){
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}

void dfs(int u){
    for(int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if(st[j]) continue;
        
        st[j] = 1;
        dist[j] = dist[u] + w[i];
        dfs(j);
    }
}

int main(){
    memset(h, -1, sizeof h);
    
    cin >> n;
    
    for(int i = 1; i < n; i ++){
        int a, b, c;
        cin >> a >> b >> c;
        
        add(a, b, c);
        add(b, a, c);
    }
    
    st[1] = 1;
    dfs(1);
    
    int k = 1;
    
    for(int i = 2, maxv = dist[1]; i <= n; i ++)
        if(maxv < dist[i]){
            maxv = dist[i];
            k = i;
        }
    
    memset(st, 0, sizeof st);
    st[k] = 1;
    dist[k] = 0;
    dfs(k);
    
    int res = dist[1];
    
    for(int i = 2; i <= n; i ++)
        res = max(res, dist[i]);
    
    
    cout << res << endl;
}