树状数组（简单版）

简单版

• 区间查询
• 单点修改

树状数组其实就是想了一种办法，用一个新的数组来维护原数组的所有信息，其中这个新数组的单点查询和区间修改都是logn级别的（而原数组的单点查询O(1), 区间修改O(n))

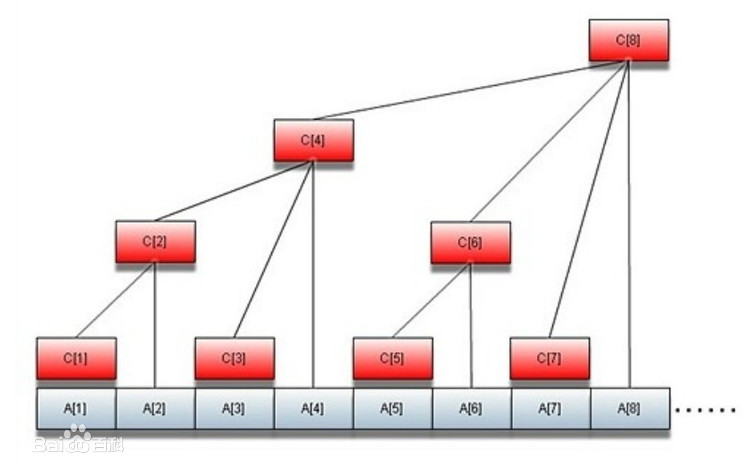
A[1~8]对应的树状数组C[1~8]的构成如图

c[1] = a[1]

c[2] = c[1] + a[2]

c[3] = a[3]

c[4] = a[4] + c[3] + c[2]

...

引用自百度百科

其实就是把单点查询搞慢了一点，把区间修改搞快了一点。

定义操作：lowbit(x) = 2^k,其中k = x低位的0的个数。

c[i]维护了\((i - lowbit(i), i]\)一段的和，是左开右闭的区间。

对于树状数组的每一个结点C[i], 可以得到C[i]的父节点为C[i + lowbit(i)]（证明复杂，略）

所以如果更新（指的是让C[i] 加上一个值或减去一个值）了C[i]，那么i~n的所有C[i]的父节点都要更新。

核心操作：query, add, lowbit

• query: 返回区间[a, b]内的元素的和
• add: 把c[i]加上x
• lowbit: return (x & -x)

#include<iostream>
using namespace std;

const int N = 100010;

int c[N], a[N];
int n, m;

int lowbit(int x){
    return x & -x;
}

void add(int x, int k){
    for(int i = k; i <= n; i += lowbit(i)) c[i] += x;
}

int query(int k){
    int res = 0;
    for(int i = k; i > 0; i -= lowbit(i)) res += c[i];
    return res;
}

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++) add(a[i], i);
    
    while(m --){
        int k, a, b;
        cin >> k >> a >> b;
        
        if(k) add(b, a);
        else cout << query(b) - query(a - 1) << endl;
    }
    
    return 0;
}

这里构造a数组的树状数组的方法很巧妙，可以这么理解：

一开始准备了一个全是0的数组的树状数组，然后对这个全零数组的i位置加上a[i],那么最后得到的就是a的树状数组了。（可以类比之前差分数组的形成）

add和query的时间复杂度较好分析

因为 \(x中1的个数 <= log_{2}x + 1，当x = 2^k - 1时，取“=”\)

所以最坏时间复杂度为\(O(log_2{n})\)