900. 整数划分

完全背包解法：

为什么想到完全背包变式？

因为划分一个整数n，只能用<= n的数字，并且一个数字可以用无限次，所以是类似于完全背包的问题。

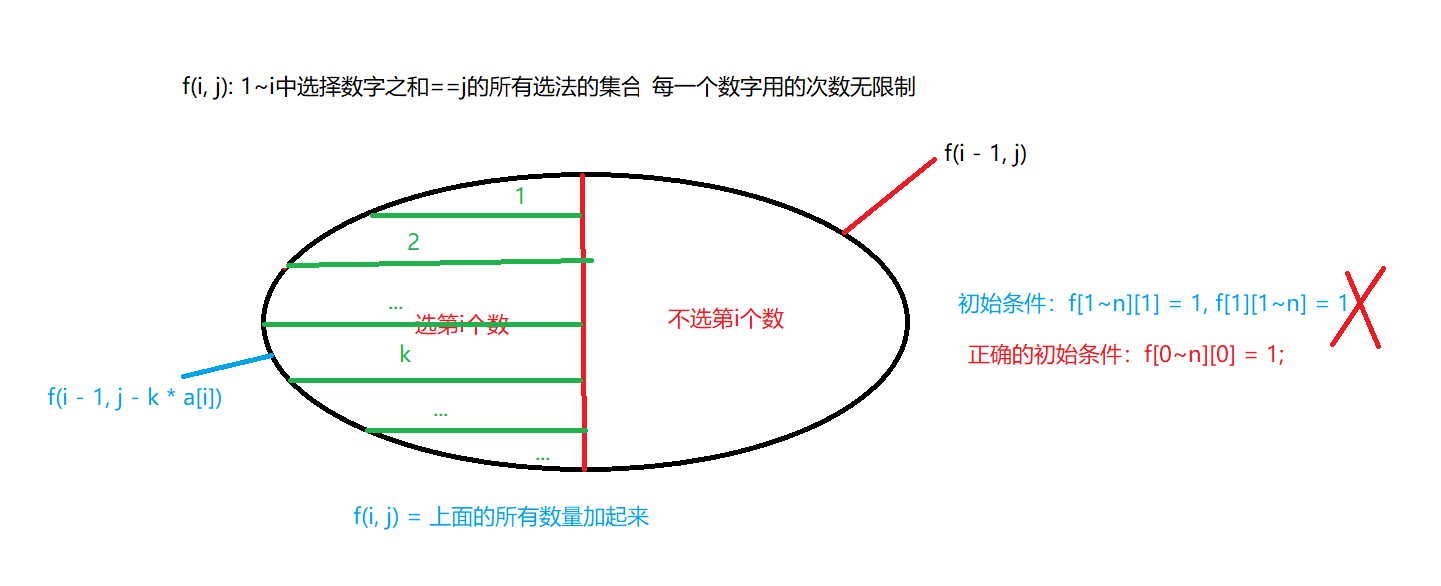
得到状态转移方程：

\(f(i, j) = f(i - 1, j) + f(i - 1, j - i) + f(i - 1, j - 2 * i) + ... + f(i - 1, j - k * i) + ...\)

朴素写法：大致是\(O(n^3)\)有TLE风险

#include<iostream>
using namespace std;

const int N = 1010, MOD = 1e9 + 7;
int f[N][N];
int n;

int main(){
    cin >> n;
    
    for(int i = 0; i <= n; i ++) f[i][0] = 1;
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= n; j ++)
            for(int k = 0; k * i <= j; k ++)
                f[i][j] = (f[i][j] + f[i - 1][j - k * i]) % MOD;
                
    cout << f[n][n];
    
    return 0;
}

从状态转移方程角度优化：

\(f(i, j) = f(i - 1, j) + f(i - 1, j - i) + f(i - 1, j - 2 * i) + ... + f(i - 1, j - k * i) + ...\\f(i, j - i) = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f(i - 1, j - i) \ \ +f(i - 1, j - 2 * i) + ... + f(i - 1, j - k*i)+...\)

所以\(f(i, j) = f(i - 1, j) + f(i, j - i)\)

#include<iostream>
using namespace std;

const int N = 1010, MOD = 1e9 + 7;
int f[N][N];
int n;

int main(){
    cin >> n;
    
    for(int i = 0; i <= n; i ++) f[i][0] = 1;
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= n; j ++){
            f[i][j] = f[i - 1][j];
            if(j >= i)
                f[i][j] = (f[i][j] + f[i][j - i]) % MOD;
        }
                
    cout << f[n][n];
    
    return 0;
}

等价变换代码

#include<iostream>
using namespace std;

const int N = 1010, MOD = 1e9 + 7;
int f[N];
int n;

int main(){
    cin >> n;
    
    f[0] = 1;
    
    for(int i = 1; i <= n; i ++)
        for(int j = i; j <= n; j ++)
            f[j] = (f[j] + f[j - i]) % MOD;
        
    cout << f[n];
    
    return 0;
}

另一个dp解法

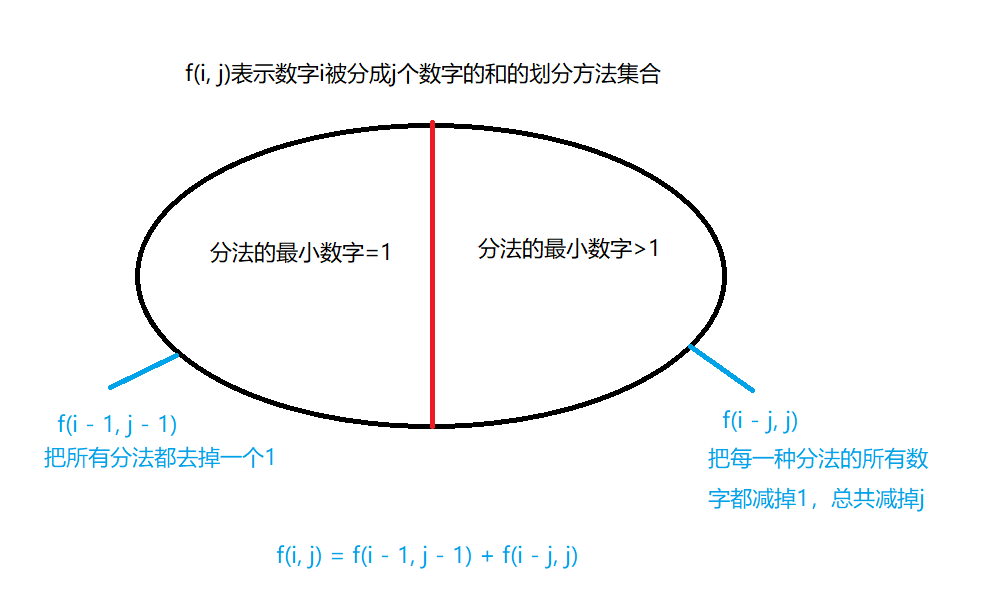
初始条件: f(0, 0) = 1

#include<iostream>
using namespace std;

const int N = 1010, MOD = 1e9 + 7;
int f[N][N];
int n;

int main(){
    cin >> n;
    
    f[0][0] = 1;

    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= i; j ++)
            f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % MOD;
                
    int res = 0;
    
    for(int i = 0; i <= n; i ++) res = (res + f[n][i]) % MOD;
    
    cout << res;
    
    return 0;
}