多重背包

多重背包：每件物品不止一个，并且有个数限制的背包问题，注意和完全背包区分。

首先确定状态\(f(i, j)表示从前i个物品中选择，并且总体积<= j的所有选法的集合，保存最大价值属性。\)

然后对\(f(i, j)进行集合划分\)

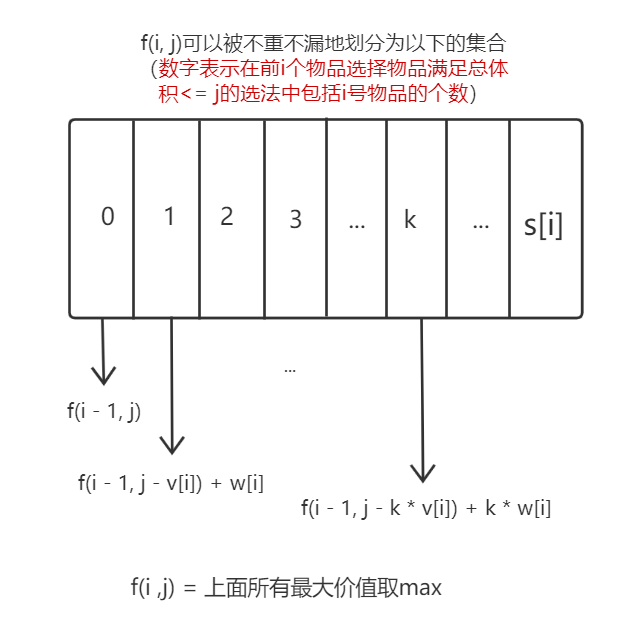
此处出现了和多重背包之间的差别，完全背包可以对i号物品的选择情况无限划分下去，直到k * v[i] > j
但是多重背包对i号物品的枚举最多只能到s[i]。

暴力写法的时间复杂度为\(O(nms)\)
当n, m, s[i]的范围比较小的时候可以写

#include<iostream>
using namespace std;

const int N = 110;

int n, m;
int f[N][N];
int w[N], v[N], s[N];


int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            for(int k = 0; k <= s[i] && k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    
    cout << f[n][m];
    
    return 0;
}

当\(n * m * s > 10^9\)时暴力超时，此时用二进制优化方法，优化复杂度到\(O(nmlog{s})\)

证明数列\(1, 2, 4, 8, 16, 32, ... , 2^k\)可以表示\(1 \sim 2^{k + 1} - 1\)的所有数

从二进制来看：\(1, 2, 4, 8, 16, 32, ... , 2^k\)分别是\(k+1\)位中的从低向高的第1~ k + 1位置1的结果，

显然，000...1~111...1都可以用这些数中的一些数的和来表示（每个数只用一次）

下面接着证明\(1, 2, 4, 8, 16, 32, ... , 2^k, C(C<2^{k + 1})\)能表示\(2^{k+1} - 1 + C\)的所有数

首先\(1, 2, 4, 8, 16, 32, ... , 2^k\)可以表示\(1 \sim 2^{k + 1} - 1\)，由于添加了一个C，那么还可以表示\(1 + C \sim 2^{k + 1} - 1 + C\)，由于\(C<2^{k+1} => C+1 <= 2^{k + 1}\)

所以\([1,2^{k + 1} - 1]\cup[C+ 1, 2^{k + 1} - 1 + C]=[1,2^{k + 1} - 1 + C]\)

由于任何数都可以改写成2^t + H（H < 2^t）的形式，所以区间右端点可以是任何整数

从而得到了多重背包的二进制优化方法

将每一种商品的数量按照以上以上数列的形式划分成新的商品转化成新的01背包问题

比如1号商品有100个，那么划分方法是1、2、4、8、16、32、37
所以1号商品被换成了5个单独的商品

时间复杂度：

把n类商品每类商品有si个的多重背包问题，转换为了商品数有\(nlogs\)的01背包问题，复杂度\(O(nmlogs)\)

#include<iostream>
using namespace std;

const int N = 11010;

int v[N], w[N];
int f[N];
int n, m;
int cnt;

int main(){
    cin >> n >> m;
    
    while(n --){
        int a, b, c; // v, w, s
        cin >> a >> b >> c;
        
        int k = 1;
        while(k <= c){
            cnt ++;
            v[cnt] = k * a;
            w[cnt] = k * b;
            c -= k;
            k <<= 1;
        }
        if(c > 0){
            cnt ++;
            v[cnt] = c * a;
            w[cnt] = c * b;
        }
    }
    
    for(int i = 1; i <= cnt; i ++)
        for(int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
            
    cout << f[m];
    
    return 0;
}