题解「「LibreOJ β Round」ZQC 的拼图」

题意

\(\text{Libre OJ}\)

分析

不难发现答案具有单调性。具体地说，设放大倍数为 \(x\)，设 \(f(x)=0\) 当且仅当不存在任何一种方案能够从 \((1,1)\) 到达 \((m,m)\)，否则 \(f(x)=1\)。一定有 \(\exists M,\forall x\geq M,f(x)=1\)。这是二分答案的经典模型。

现在考虑如何根据一个确定的放大倍数 \(mid\) 判断是否有解。或许我们会纠结三角形的摆放次序对答案有无影响，不妨把每个三角形可以到达的区域看作一些向量，那么向量的先后顺序时不影响答案的。这样就可以暴力 \(\text{DP}\)，设 \(f_{i,x,y}\) 为前 \(i\) 个三角形能 \(/\) 不能到达 \((x,y)\)，时间复杂度为 \(O(nm^4 \log V)\)，其中 \(V\) 为二分的上界，在题目中为 \(2m\times \max\{a_i,b_i\}\)，即仅需摆放一个三角形就可以从 \((1,1)\) 到 \((m,m)\) 的情况。

这个时间复杂度显然爆炸。我们发现，很多时候判定性 \(\text{DP}\) 都可以转化成最优性 \(\text{DP}\)，那我们就顺着这个思路想。可以发现一个单调性，如果摆放完一些拼图能够到达 \((i,j)\)，那么将这些拼图换种方式摆放，也能够到达 \(\forall k\leq j,(i,k)\)。于是设 \(f_{i,j}\) 为前 \(i\) 块拼图能够到达的 \((j,k)\) 中 \(k\) 的最大值。形式化的说：

\[f_{i,j}=\max\{k|用前 \ i \ 块拼图可以到达 \ (j,k)\} \]

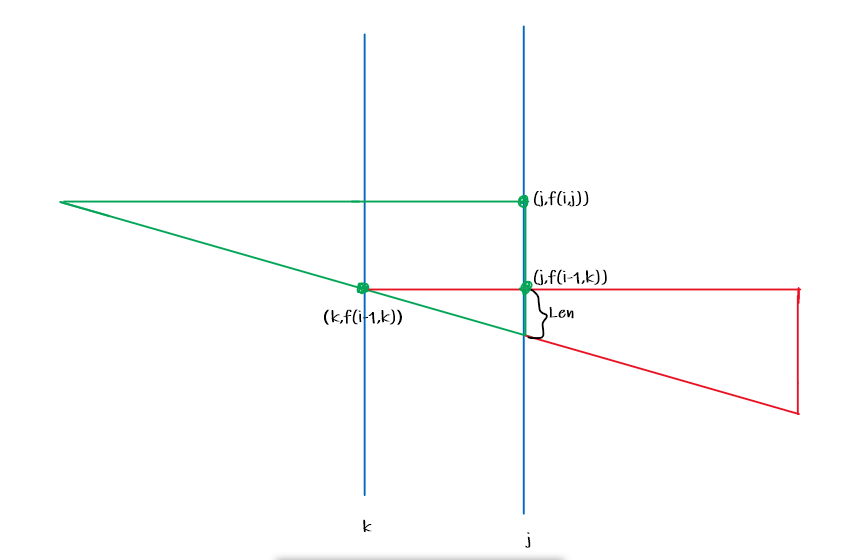
上图中，三角形由红色部分移至绿色部分，两点间始终连通，但到达的范围扩大。

根据上图，卡一下三角形平移过程中对于两个点的边界情况，使用相似三角形计算贡献，得到下述转移方程：

\[f(i,j)=\max_{\max(0,j-\left\lfloor\frac{mid}{a_i}\right\rfloor)\leq k\leq j}\left\{f(i-1,k)+\left\lfloor\frac{mid-a_i(j-k)}{b_i}\right\rfloor\right\} \]

时间复杂度降为 \(O(nm^2 \log V)\)，空间复杂度可以通过滚动降为 \(O(m)\)。

代码

#include<cstdio>
int n,m;
int f[105][105],a[105],b[105];
inline int read() {
    register int x=0,f=1;register char s=getchar();
    while(s>'9'||s<'0') {if(s=='-') f=-1;s=getchar();}
    while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
    return x*f;
}
inline int max(const int &x,const int &y) {return x>y? x:y;}
inline bool check(int mid) {
    f[0][0]=0; for(register int i=1;i<=m;++i) f[0][i]=-1e9; //f[0][1]=1;
    for(register int i=1;i<=n;++i) {
        for(register int j=m;j>=0;--j) {
            f[i][j]=-1e9;
            for(register int k=max(0,j-mid/a[i]);k<=j;++k) {
                f[i][j]=max(f[i][j],f[i-1][k]+(mid-a[i]*(j-k))/b[i]);
            }
        }
    }
    return f[n][m]>=m;
}
int main() {
    n=read();m=read(); int mx=1;
    for(register int i=1;i<=n;++i) {a[i]=read();b[i]=read();mx=max(mx,max(a[i],b[i]));}
    int l=1,r=2*m*mx,res=1;
    while(l<=r) {
        int mid=l+r>>1;
        if(check(mid)) res=mid,r=mid-1;
        else l=mid+1;
    }
    printf("%d\n",res);
    return 0;
}