CSP-S初赛模拟_整理及总结

提高组CSP-S2024初赛模拟卷1

由于工作量太大，故没有使用LaTeX！

1. 表达式(8 %(-6))与(-8 % 6)的值为 B.2,-2 。

被除数是正数，余数是正数；被除数是负数，余数是负数。

2. 设根结点深度为0，一棵深度为 h 的满三叉树，即除最后一层无任何子结点外，每一层上的所有结点都有3个子结点的树，共有多少节点。 A.(3^(h+1)-1)/2

第h层有3^{h个节点，把3}h当做单位一，往前每一层为1/3,1/9,1/27....可以发现最后的和接近于3/2，实际为最后一层的3/2减去第0层的1/2，因为第零层只有一个节点，所以就为1/2，所以h层共有(3^(h+1)-1)/2个节点。

3. 以下不属于调试工具 GDB 中的命令的是 A.printf 。
   A.printf
   B.display
   C.next
   D.step

GDB是Linux和许多类Unix系统的标准开发环境，可以调试C、C++、Go、java等语言的程序。

命令/函数	功能
printf	C 库函数 int printf(const char *format, ...) 发送格式化输出到标准输出 stdout。
display	使用 display 命令查看变量或表达式的值，如：(gdb) display expr
next	next 命令（简写为 n）是让 GDB 调到下一条命令去执行，不一定是代码下一行
step	step 命令和 next 命令的功能相同，都是单步执行程序。不同之处在于，当 step 命令所执行的代码行中包含函数时，会进入该函数内部，并在函数第一行代码处停止执行。

4. 以下哪个不属于算法的最本质特征？C.先进性
   A.有穷性
   B.确定性
   C.先进性
   D.确切性

算法的特征包括：

• 有穷性：执行步骤有限，必须终止。
• 确定性：每步骤有确切定义。
• 输入：有0个或多个输入。
• 输出：有一个或多个输出。
• 可行性：每步骤可分解为可执行的操作步，即有效性。

5. 以下哪个不属于哈希冲突的常见处理方法？D.固定分配法
   A.哈希法
   B.线性探查法
   C.二次探查法
   D.固定分配法

哈希冲突的处理方法包括：

• 链地址法：每个哈希桶中存储一个链表或其他数据结构，来存储所有映射到相同桶的键值对。
• 开放地址法：将键值对放置到其他可用的哈希桶中，如线性探测、二次探测等方法。
• 再哈希法：同时构造多个不同的哈希函数，重新映射键值对。

哈希法可以被视为链地址法、开放地址法和再哈希法的总称。

6. 单源最短路问题的常用算法不包含 D.Kruskal 。
   A.Bellman-Ford
   B.Dijkstra
   C.SPFA
   D.Kruskal

算法	用途
Bellman-Ford	用于找到图中两点间的最短路径，能处理含有负权边的情况，包括检测负权环
Dijkstra	求有权图中最短路径的标号法
SPFA	一种求解单源最短路径问题的算法
Kruskal	最小生成树算法,基本思想是从小到大加入边，是个贪心算法。

7. 设某算法的时间复杂度函数的递推方程是 F(n）= F(n－ 1）+ 2n（n为正整数)
   及F(0)=0，则该算法的时间复杂度为 C.O(n^2) 。
   A. O(logn)
   B. O(n)
   C. O(n^2)
   D. O(nlogn)

F(n)=(F(n-2)+2n-2)+2n=F(n-2)+4n-2

F(n)=(F(n-3)+2n-4)+4n-2=F(n-3)+6n-6

F(n)=(F(n-4)+2n-6)+6n-6=F(n-4)+8n-12

F(n)=F(n-n)+2(n^{2)-n(n-1)=2(n}2)-n²⁺¹⁼ⁿ2+1

8. 一棵二叉树一共有 19个结点，其叶子结点不可能有 A.11 个。
   A.11
   B.10
   C.9
   D.1

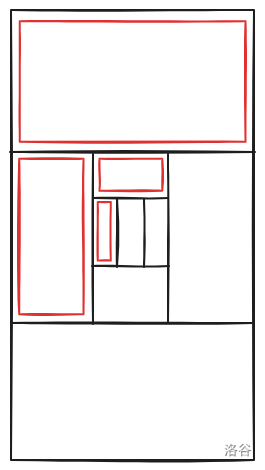
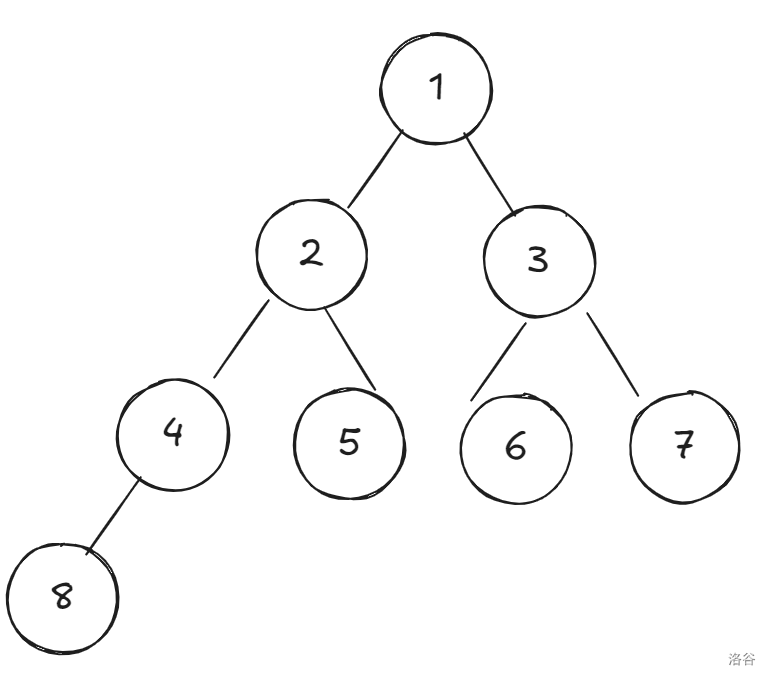
如果有11个叶子结点，那么就有19-11=8个非叶子节点，使得最后能放的叶子结点最多的结构如下图，此时最多能放9个叶子结点，放不了11个节点，故不行。其余同理，都可以放得下。

9. 关于拓扑排序，下面的说法哪个是正确的？C.拓扑排序一定从入度为0的结点开始
   A.拓扑排序只能用广度优先遍历实现
   B.每个有向图都至少存在一个拓扑排序
   C.拓扑排序一定从入度为0的结点开始
   D.拓扑排序的方案一定是唯一的

• 拓扑排序也可以使用dfs实现，dfs序就是拓扑序。
• 带环有向图不存在拓扑序。
• 只有入度为0的点不受制约。
• 当有多个入读为0的点时，任意一个即可，故有多个拓扑序。

10. 下列说法中哪个不是树的性质？B.树中有可能有一个简单环
    A.任意两个结点之间有且只有一条简单路径
    B.树中有可能有一个简单环
    C.边的数目恰好是顶点数目减1
    D.树中无环

• 简单路径：路径上的各顶点均不互相重复。只有一条，即经过LCA的路径。
• 树中无环

11. 对于完全背包问题（给出n种物品和一个容积为m的背包，每种物品有无限个，单个大小为v[i]，价值为w[i]，要求选择合适的物品放入背包，满足大小不超过容积且价值最大)，设f[i]表示用去i的空间能获得的最大价值，倒序枚举i为使用的空间，正序枚举j为物品编号，则可写出动态转移方程。
    A. f[i] = max(f[i], f[i-w[j]] + v[j])
    B. f[i] = max(f[i], f[i-v[j]] + w[j])
    C. f[i] = min(f[i], f[i-w[j]] + v[j])
    D. f[i] = min(f[i], f[i-v[j]] + w[j])