[2024-08-19]CSP-S初赛复习
CSP-S初赛复习
ASCII码
| 字符 | ASCII码 |
|---|---|
| 'a' | 97 |
| 'A' | 65 |
| '1' | 49 |
| 空格:' ' | 32 |
Linux相关
基础命令
| 命令 | 功能 |
|---|---|
| cd | 进入目录 |
| ls | 列出工作目录所含的文件和子目录 |
| pwd | 显示目前的目录 |
| mkdir | 创建文件夹 |
| rmdir | 删除空文件夹 |
| touch | 创建空白文件 |
| cp | 复制文件或目录 |
| rm | 删除文件或目录(包括目录内所有文件) |
| mv | 移动文件或目录 |
| file | 查看文件类型 |
| man | 查看命令使用文档 |
Linux time 指令
- 引用于 CSDN Linux time命令用法
Linux time命令是一个非常实用的工具,主要用于计算程序执行的时间。这个命令可以用来度量一段代码或者脚本的运行时间,有助于性能调优和基准测试。
- 例子:
time -p ls,time -v ls。 - -p:以可移植输出格式打印实际时间、用户 CPU 时间和系统 CPU 时间。
- -v:提供更详细的信息,包括进程使用的系统资源。
通常输出三种时间:
-
real(实际时间)
从开始到结束的墙钟时间(wall-clock time)。也就是我们常说的实际时间。 -
user(用户CPU时间)
在用户模式中执行该过程所花费的CPU时间。 -
sys(系统CPU时间)
在内核模式中执行该过程所花费的CPU时间。
情景
[root@localhost home]# time -p ls
centos docker keen mc woakioi woakioi1
real 0.00
user 0.00
sys 0.00
[root@localhost home]# \time -v ls
centos docker keen mc woakioi woakioi1
Command being timed: "ls"
User time (seconds): 0.00
System time (seconds): 0.00
Percent of CPU this job got: 100%
Elapsed (wall clock) time (h:mm:ss or m:ss): 0:00.00
Average shared text size (kbytes): 0
Average unshared data size (kbytes): 0
Average stack size (kbytes): 0
Average total size (kbytes): 0
Maximum resident set size (kbytes): 2576
Average resident set size (kbytes): 0
Major (requiring I/O) page faults: 0
Minor (reclaiming a frame) page faults: 120
Voluntary context switches: 1
Involuntary context switches: 0
Swaps: 0
File system inputs: 0
File system outputs: 0
Socket messages sent: 0
Socket messages received: 0
Signals delivered: 0
Page size (bytes): 4096
Exit status: 0
-
一般情况 \(real=user+sys\) 。
-
多核处理器 \(real<user+sys\) 。因为多个CPU核心可以同时工作,或者说导致实际时间变少。
-
有他进程占用时 \(real>user+sys\) 。
GCC/G++编译命令
-
如果你编写的是 C 代码,使用
gcc。 -
如果你编写的是 C++ 代码,使用
g++。 -
CSDN:GCC编译常用命令 。
| 选项 | 功能 |
|---|---|
-o |
指定输出文件名。例如,-o myprogram 表示将输出文件命名为 myprogram。 |
-c |
只编译,不链接,生成目标文件(.o 文件)。 |
-Wall |
全称"Warn All" ,启用所有警告信息,帮助发现潜在问题。 |
-Werror |
全称 "Warnings as Errors",将所有警告视为错误,编译失败。 |
-g |
生成调试信息,便于使用调试器(如 gdb)调试程序。 |
-std |
指定 C++ 标准版本,例如 -std=c++11、-std=c++14、-std=c++17。 |
-I |
指定头文件搜索路径。例如,-I/path/to/include。 |
-L |
指定库文件搜索路径。例如,-L/path/to/lib。 |
-l |
链接指定的库。例如,-lm 链接数学库。 |
-static |
进行静态链接,生成不依赖于共享库的可执行文件。 |
-fPIC |
生成位置无关代码,通常用于创建共享库。 |
-O |
启用优化,-O1、-O2、-O3 分别表示不同级别的优化。 |
-S |
只编译源文件,生成汇编代码(.s 文件)。 |
-E |
只进行预处理,输出预处理后的代码。 |
CCF考点编译环境:-O2 -std=C++14
进制转换
- 二进制:C和C++都没有提供二进制数的表达方法。
- 八进制:C/C++中为了区分,以
0开头。 - 十六进制:C/C++为了区分,以
0x开头。
十进制转X进制
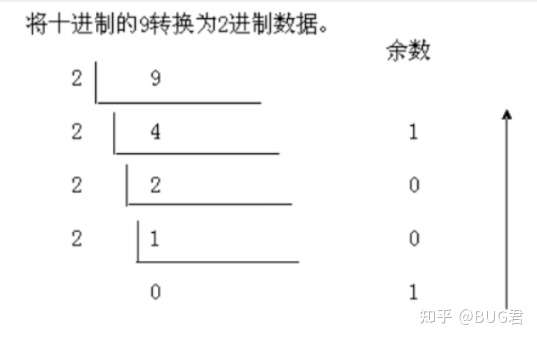
小数转化
十进制转X进制
十进制小数转换成二进制小数采用 “乘2取整,顺序输出” 法。
- 例子:

0.618D = 0.101B(保留三位小数)
X进制转十进制
把X进制数按权展开、相加即得十进制数。
- 例子:

排序算法
- 排序算法的稳定性
- 8大排序算法的稳定和不稳定分析:CSDN。
稳定性是指相等的元素经过排序之后相对顺序是否发生了改变。
-
笔者总结的规律:时间复杂度带\(log_2n\)的一般不稳定,归并排序除外。除此之外有交换操作且相邻两个交换的一般稳定,反之,交换的两元素距离太大一般不稳定。
-
常见排序算法
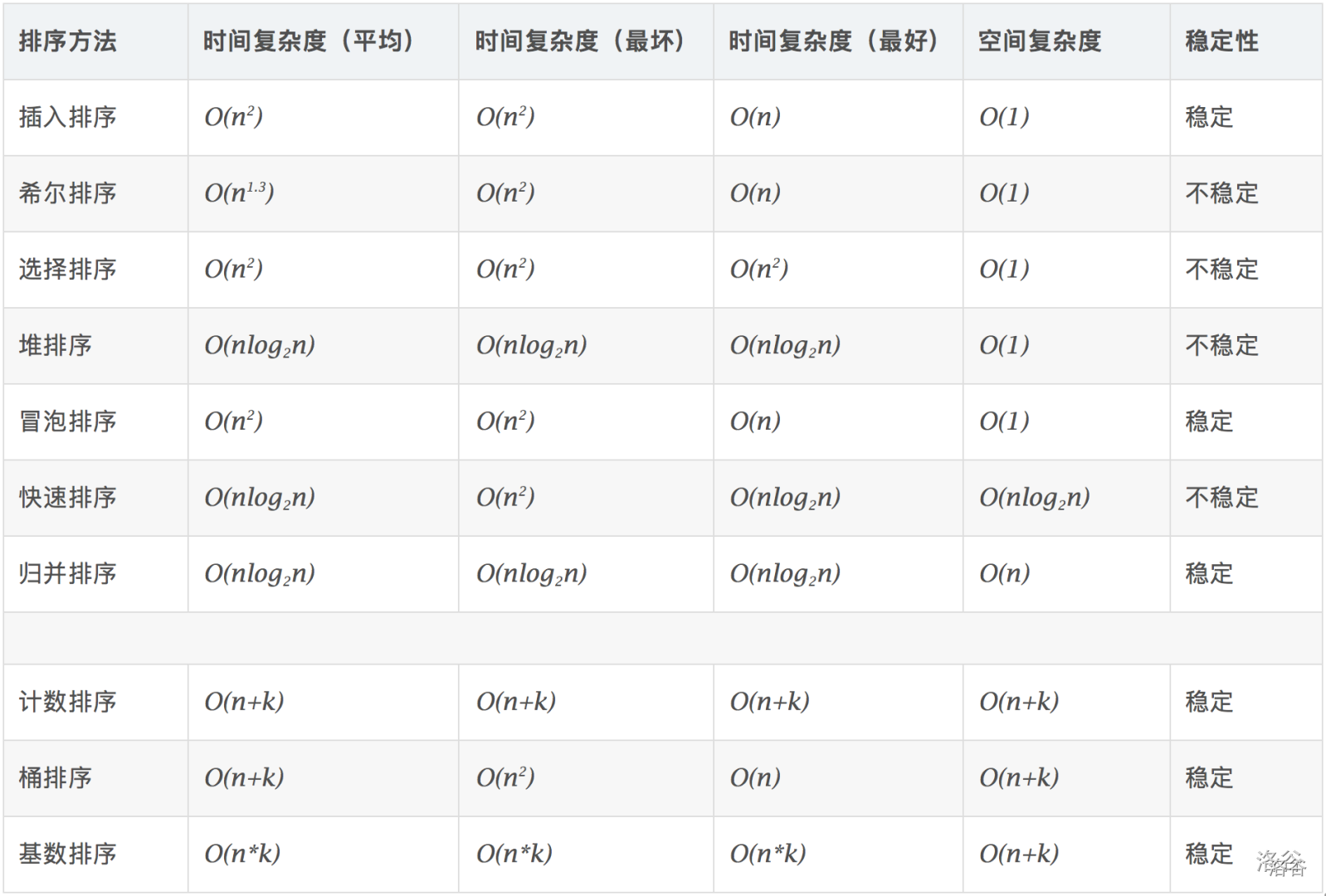
- \(n\) 是待排序元素的数量。
- \(k\) 是元素值的范围。
插入排序
插入排序是一种简单的排序算法,适用于小规模数据的排序。它的基本思想是将待排序的元素逐个插入到已排序的序列中,直到所有元素都被插入为止。
- 最坏情况:\(O(n²)\)(当输入数组是逆序时)
- 最好情况:\(O(n)\)(当输入数组已经是有序时)
- 平均情况:\(O(n²)\)
- bilibili 可视化插入排序。
希尔排序
希尔排序是一种基于插入排序的排序算法,通过将数据分成多个子序列来进行排序,从而提高插入排序的效率。它的基本思想是先对间隔为 h 的元素进行插入排序,然后逐步缩小间隔,最终对整个序列进行插入排序。
- 最坏情况:\(O(n²)\)(具体取决于增量序列的选择)
- 最好情况:\(O(n log n)\)(当输入数组接近有序时)
- 平均情况:\(O(n log n)\)(具体取决于增量序列的选择)
- bilibili 可视化希尔排序。(建议观看)
选择排序
选择排序的基本思想是每次从未排序的部分中选择最小(或最大)元素,将其放到已排序部分的末尾。该过程重复进行,直到所有元素都被排序。
- 最坏情况:\(O(n²)\)
- 最好情况:\(O(n²)\)
- 平均情况:\(O(n²)\)
- bilibili 可视化选择排序。
堆排序
堆排序利用堆这种数据结构来进行排序。它的基本思想是将待排序的数组构建成一个最大堆(或最小堆),然后反复将堆顶元素(最大或最小)移到数组的末尾,逐步缩小堆的范围。
- 最坏情况:\(O(n log n)\)
- 最好情况:\(O(n log n)\)
- 平均情况:\(O(n log n)\)
- bilibili 可视化堆(数据结构)。
- bilibili 可视化生成最大堆算法。
- bilibili 可视化最大堆维护算法。
- bilibili 可视化堆排序算法。
冒泡排序
冒泡排序是一种简单的排序算法,通过重复遍历待排序的数组,比较相邻元素并交换它们的顺序,直到没有需要交换的元素为止。该算法因其每次遍历都将最大(或最小)元素“冒泡”到数组的一端而得名。
- 最坏情况:\(O(n²)\)
- 最好情况:\(O(n)\)(当数组已经有序时)
- 平均情况:\(O(n²)\)
- bilibili 可视化冒泡排序。
快速排序
快速排序是一种高效的排序算法,采用分治法(Divide and Conquer)策略。它的基本思想是通过一个“基准”元素将数组分为两部分,左边部分的元素都小于基准,右边部分的元素都大于基准,然后递归地对这两部分进行排序。
- 最坏情况:\(O(n²)\)(当数组已经有序或逆序时)
- 最好情况:\(O(n log n)\)
- 平均情况:$O(n log n) $
- bilibili 可视化快速排序(只展示了其中一种,快速排序有很多实现方法)。
- 快速排序是不稳定排序。如果随机选择基准数则会导致排序不稳定,但如果每次都选定头部位置,那么这不会导致排序的不稳定。另一个原因是在快速排序过程中,在 \(i\) 指针左边的数都小于基准,右边的数都大于等于基准的时候,这个时候我们需要交换 \(a[i]\) 和 \(a[t]\)(基准数),一旦 \(i\) 和 \(t\) 之间有和 \(a[t]\) 相等的数,那么这个操作就破坏了排序的稳定性。
归并排序
归并排序是一种基于分治法的排序算法。它将数组分成两个子数组,分别对这两个子数组进行排序,然后将已排序的子数组合并成一个最终的排序数组。
-
最坏情况:\(O(n log n)\)
-
最好情况:\(O(n log n)\)
-
平均情况:\(O(n log n)\)
-
bilibili 可视化归并排序。
计数排序
计数排序是一种非比较的排序算法,适用于范围有限的整数排序。它的基本思想是通过统计每个元素出现的次数,然后根据这些计数来确定每个元素在排序后数组中的位置。
- 时间复杂度:\(O(n + k)\),其中 \(n\) 是待排序元素的数量,\(k\) 是元素值的范围。
- 空间复杂度:\(O(k)\)
- bilibili 可视化计数排序。
桶排序
桶排序是一种分布式排序算法,适用于均匀分布的数据。它的基本思想是将数据分到有限数量的桶中,然后对每个桶内的数据进行排序,最后将所有桶中的数据合并。
- 时间复杂度:\(O(n + k)\),其中 \(n\) 是待排序元素的数量,\(k\) 是桶的数量(在理想情况下,桶内元素数量较少时)。
- 空间复杂度:\(O(n + k)\)
- bilibili 可视化桶排序。
基数排序
基数排序是一种非比较的排序算法,适用于整数或字符串的排序。它通过将数据分成不同的“桶”来进行排序,通常是按位进行排序,从最低位到最高位。
- 时间复杂度:\(O(n * k)\),其中 \(n\) 是待排序元素的数量,\(k\) 是数字的位数。
- 空间复杂度:\(O(n + k)\)
- bilibili 可视化基数排序。
二进制数的原码、反码、补码
根据冯·诺依曼提出的经典计算机体系结构框架,一台计算机由运算器、控制器、存储器、输入和输出设备组成。其中运算器只有加法运算器,没有减法运算器。
从硬件的角度上看,只有正数加负数才算减法,正数与正数相加,负数与负数相加,其实都可以通过加法器直接相加。
符号位在内存中存放的最左边一位,如果该位为0,则说明该数为正;若为1,则说明该数为负。
原码、反码、补码的产生过程就是为了解决计算机做减法和引入符号位的问题。
- 正数的原码、反码、补码都一致,只有负数不同。
原码
原码:是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值。
| 数值 | 二进制原码 | 数值 | 二进制原码 |
|---|---|---|---|
| 1 | 0001 | -1 | 1001 |
| 2 | 0010 | -2 | 1010 |
| 3 | 0011 | -3 | 1011 |
| 4 | 0100 | -4 | 1100 |
| 5 | 0101 | -5 | 1101 |
反码
负数的反码就是它的原码除符号位外,按位取反,即对应正数取反。
为什么要有反码? 为了解决原码做减法的问题
| 数值 | 二进制原码 | 数值 | 二进制原码 |
|---|---|---|---|
| 1 | 0001 | -1 | 1110 |
| 2 | 0010 | -2 | 1101 |
| 3 | 0011 | -3 | 1100 |
| 4 | 0100 | -4 | 1011 |
| 5 | 0101 | -5 | 1010 |
补码
负数的补码等于反码+1,即对应正数取反加一。
为什么要有补码? 为了解决正负0同一个编码的问题
| 数值 | 二进制原码 | 数值 | 二进制原码 |
|---|---|---|---|
| 1 | 0001 | -1 | 1111 |
| 2 | 0010 | -2 | 1110 |
| 3 | 0011 | -3 | 1101 |
| 4 | 0100 | -4 | 1100 |
| 5 | 0101 | -5 | 1011 |
负数运算
存在争议,对于CSP-S初赛,纯数学题使用数学定义,程序题参考C++的计算结果。
| C++ | Java | Python | 百度 | 谷歌 | |
|---|---|---|---|---|---|
| 7 mod 3 | 1 | 1 | 1 | 1 | 1 |
| (-7) mod 3 | -1 | -1 | 2 | 2 | 2 |
| 7 mod (-3) | 1 | 1 | -2 | -2 | -2 |
| (-7) mod (-3) | -1 | -1 | -1 | -1 | -1 |
C++下,对于 $A, B \in \mathbb{Z}^+ $ :
- $(-A)%(-B)=-(A%B) $
- $(-A)%B = -(A%B) $
- $A%(-B) = A%B $
即:结果的正负由 \(A\) 的正负决定,而结果的绝对值\(=|A|\%|B|\)。
- 数学定义 :\(x\%y=x-y\lfloor \dfrac{x}{y}\rfloor\)。
位运算
按位与(&)
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1
用途:
- 清零:如果想将一个单元清零,只要与一个各位都为零的数值相与,结果为零。
- 取一个数的指定位:例如,取数
X = 1010 1110的低4位,只需另找一个数Y = 0000 1111,然后X & Y = 0000 1110即可得到X的指定位。 - 判断奇偶:通过判断最未位是0还是1来决定奇偶,可以用
if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是否为偶数。
按位或(|)
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
用途:
- 设置某些位为1:例如,将数
X = 1010 1110的低4位设置为1,只需另找一个数Y = 0000 1111,然后X | Y = 1010 1111即可得到。
异或(^)
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0
性质:
- 交换律
- 结合律:
(a ^ b) ^ c == a ^ (b ^ c) - 对于任何数
x,都有x ^ x = 0,x ^ 0 = x - 自反性:
a ^ b ^ b = a ^ 0 = a
用途:
- 翻转指定位:例如,将数
X = 1010 1110的低4位翻转,只需另找一个数Y = 0000 1111,然后X ^ Y = 1010 0001即可得到。 - 与0相异或值不变:例如
1010 1110 ^ 0000 0000 = 1010 1110 - 交换两个数:
void Swap(int &a, int &b)
{
if (a != b)
{
a ^= b;
b ^= a;
a ^= b;
}
}
取反(~)
~1 = 1111 1110
~0 = 1111 1111
用途:
- 使一个数的最低位为零:例如,使
a的最低位为0,可以表示为:a & ~1。~1的值为1111 1111 1111 1110,再按"与"运算,最低位一定为0。
左移(<<)
设
a = 1010 1110,a = a << 2将a的二进制位左移2位、右补0,即得a = 1011 1000。
右移(>>)
操作数每右移一位,相当于该数除以2。
复合赋值运算符
a &= b相当于a = a & ba |= b相当于a = a | ba >>= b相当于a = a >> ba <<= b相当于a = a << ba ^= b相当于a = a ^ b
大端和小端模式
大端(Big-endian)和小端(Little-endian)是两种不同的字节序(byte order)表示方式,主要用于多字节数据(如整数、浮点数等)的存储和传输。
大端模式(Big-endian)
-
在大端模式中,数据的高位字节存储在低地址,低位字节存储在高地址。
-
例如,32位整数
0x12345678在内存中的存储顺序为:地址: 0x00 0x01 0x02 0x03 数据: 0x12 0x34 0x56 0x78
小端模式(Little-endian)
-
在小端模式中,数据的低位字节存储在低地址,高位字节存储在高地址。
-
例如,32位整数
0x12345678在内存中的存储顺序为:地址: 0x00 0x01 0x02 0x03 数据: 0x78 0x56 0x34 0x12
应用场景
- 大端模式:通常用于网络协议(如TCP/IP),因为它符合人类阅读的顺序。
- 小端模式:常见于x86架构的计算机系统(如Intel处理器),因为它在某些情况下可以提高性能。
总结
选择大端或小端模式取决于具体的应用需求和硬件架构。在进行数据传输或存储时,了解字节序是非常重要的,以确保数据的正确解析和处理。
数据结构及相关算法
队列(Queue)
队列是一种数据结构,遵循先进先出(FIFO, First In First Out)的原则。即,最先插入队列的元素最先被移除。队列常用于需要按顺序处理数据的场景。
基本操作:
- 入队(Enqueue):将元素添加到队列的尾部。
- 出队(Dequeue):从队列的头部移除元素,并返回该元素。
- 查看队头(Front):返回队列头部的元素,但不移除它。
- 检查队列是否为空(IsEmpty):判断队列是否包含元素。
- 获取队列大小(Size):返回队列中元素的数量。
特点:
- 顺序性:元素的处理顺序与插入顺序一致。
- 动态性:队列可以根据需要动态扩展,通常实现为链表或数组。
应用场景:
- 任务调度:操作系统中的任务管理。
- 数据缓冲:如打印队列、IO缓冲区。
- 广度优先搜索:图算法中的节点访问顺序。
链表(Linked List)
链表是一种动态数据结构,由一系列节点组成,每个节点包含数据和指向下一个节点的指针。与数组不同,链表的大小可以动态变化,适合频繁插入和删除操作的场景。
基本结构:
- 节点(Node):链表的基本单元,通常包含两个部分:
- 数据部分(Data)
- 指针部分(Next),指向下一个节点
类型:
- 单向链表(Singly Linked List):每个节点只指向下一个节点。
- 双向链表(Doubly Linked List):每个节点有两个指针,分别指向前一个节点和下一个节点。
- 循环链表(Circular Linked List):最后一个节点指向头节点,形成一个环。
基本操作:
- 插入(Insert):在链表的任意位置插入新节点。
- 删除(Delete):从链表中删除指定节点。
- 查找(Search):查找链表中是否存在某个值。
- 遍历(Traverse):访问链表中的每个节点。
栈(Stack)
栈是一种数据结构,遵循后进先出(LIFO, Last In First Out)的原则。即,最后插入栈的元素最先被移除。栈常用于需要按顺序处理数据的场景,如函数调用和表达式求值。
基本操作:
- 入栈(Push):将元素添加到栈的顶部。
- 出栈(Pop):移除并返回栈顶部的元素。
- 查看栈顶元素(Top/Peek):返回栈顶部的元素,但不移除它。
- 检查栈是否为空(IsEmpty):判断栈是否包含元素。
- 获取栈的大小(Size):返回栈中元素的数量。
特点:
- 顺序性:元素的处理顺序与插入顺序相反。
- 动态性:栈可以根据需要动态扩展,通常实现为链表或数组。
应用场景:
- 函数调用管理:维护函数调用的返回地址和局部变量。
- 表达式求值:用于解析和计算算术表达式。
- 撤销操作:在应用程序中实现撤销功能,如文本编辑器。
图(Graph)
图是一种数据结构,由一组顶点(节点)和一组边(连接顶点的线)组成。图可以用来表示各种关系,如社交网络、城市之间的道路、网络拓扑等。图可以是有向的或无向的,边可以是加权的或非加权的。
基本术语:
- 顶点(Vertex):图中的基本单位,表示对象。
- 边(Edge):连接两个顶点的线,表示对象之间的关系。
- 有向图(Directed Graph):边有方向,从一个顶点指向另一个顶点。
- 无向图(Undirected Graph):边没有方向,表示两个顶点之间的双向关系。
- 加权图(Weighted Graph):边带有权重,表示连接的强度或成本。
- 邻接矩阵(Adjacency Matrix):用二维数组表示图的边关系。
- 邻接表(Adjacency List):用链表或数组表示每个顶点的邻接顶点。
基本操作:
- 添加顶点(Add Vertex):向图中添加一个新顶点。
- 添加边(Add Edge):在两个顶点之间添加一条边。
- 删除顶点(Remove Vertex):从图中删除一个顶点及其相关边。
- 删除边(Remove Edge):从图中删除一条边。
- 遍历图(Traverse):访问图中的所有顶点,常用的方法有深度优先搜索(DFS)和广度优先搜索(BFS)。
特点:
- 灵活性:图可以表示复杂的关系和结构。
- 多样性:图的类型多样,适用于不同的应用场景。
应用场景:
- 社交网络:表示用户之间的关系。
- 地图导航:表示城市和道路之间的连接。
- 网络流:用于流量分析和优化。
- 推荐系统:通过用户和物品之间的关系进行推荐。
树(Tree)
树是一种层次型数据结构,由节点组成,具有一个根节点和零个或多个子节点。树的每个节点可以有多个子节点,但每个节点只有一个父节点(根节点除外)。树常用于表示分层关系,如文件系统、组织结构等。
特征
- 节点(Node):树由多个节点组成,每个节点可以存储数据。
- 根节点(Root):树的顶层节点,唯一且没有父节点。
- 叶子节点(Leaf):
- 无根树的叶节点:度数不超过 1 的节点。
- 有根树的叶节点:没有子节点的节点。
- 子节点(Child):某个节点的下级节点。
- 父节点(Parent):某个节点的上级节点。
- 深度(Depth):节点到根节点的路径长度。
- 高度(Height):节点到其最远叶子节点的路径长度。
- 子树(Subtree):某个节点及其所有后代节点组成的树。
数学定义
- 定义:一个树是一个无向图 ( T ),满足以下条件:
- ( T ) 是连通的。
- ( T ) 不包含环。
- 如果 ( T ) 有 ( n ) 个节点,则 ( T ) 有 ( n-1 ) 条边。
特殊类型的树
- 二叉树(Binary Tree):每个节点最多有两个子节点(左子节点和右子节点)。
- 平衡树(Balanced Tree):树的高度尽可能小,以保证操作的效率。
- 搜索树(Search Tree):节点的值满足特定的顺序关系,便于查找。
二叉树的类型
- 满二叉树(Full Binary Tree):每个节点要么是叶子节点,要么有两个子节点。
- 完全二叉树(Complete Binary Tree):除了最后一层外,其他层的节点都被填满,且最后一层的节点从左到右排列。
- 平衡二叉树(Balanced Binary Tree):任意节点的左右子树高度差不超过 1。
- 二叉搜索树(Binary Search Tree, BST):对于每个节点,左子树的所有节点值小于该节点值,右子树的所有节点值大于该节点值。
森林与生成树
- 森林(Forest):由多个连通分量(连通块)组成的图,每个连通分量都是树。根据定义,一棵树也是森林。
- 生成树(Spanning Tree):一个连通无向图的生成子图,同时要求是树。即在图的边集中选择 ( n-1 ) 条边,将所有顶点连通。
基本操作
- 插入(Insert):在树中添加新节点。
- 删除(Delete):从树中移除节点。
- 查找(Search):查找树中是否存在某个值。
- 遍历(Traverse):访问树中的所有节点,常用的方法有前序遍历、中序遍历和后序遍历。
树的遍历
树的遍历是访问树中所有节点的过程,常用的遍历方法有三种主要类型:前序遍历、中序遍历和后序遍历。每种遍历方法都有其特定的访问顺序。
1. 前序遍历(Pre-order Traversal)
访问顺序:根节点 -> 左子树 -> 右子树
算法步骤:
- 访问根节点。
- 递归前序遍历左子树。
- 递归前序遍历右子树。
2. 中序遍历(In-order Traversal)
访问顺序:左子树 -> 根节点 -> 右子树
算法步骤:
- 递归中序遍历左子树。
- 访问根节点。
- 递归中序遍历右子树。
3. 后序遍历(Post-order Traversal)
访问顺序:左子树 -> 右子树 -> 根节点
算法步骤:
- 递归后序遍历左子树。
- 递归后序遍历右子树。
- 访问根节点。
4. 层次遍历(Level-order Traversal)
访问顺序:按层次从上到下、从左到右访问每一层的节点。
算法步骤:
- 使用队列(Queue)来存储节点。
- 访问队列中的节点,依次将其子节点加入队列。
特点
- 层次性:树的结构反映了数据的层次关系。
- 递归性:树的定义和操作通常使用递归方法。
应用场景
- 文件系统:表示文件和目录的层次结构。
- 数据库索引:如 B 树和红黑树,用于快速查找。
- 表达式树:用于表示和计算数学表达式。
- 决策树:用于分类和回归分析。
堆(Heap)
堆是一种特殊的树形数据结构,通常用于实现优先队列。堆具有以下特征:
-
完全二叉树:堆是一种完全二叉树,除了最后一层外,其他层的节点都被填满,最后一层的节点从左到右排列。
-
堆性质:
- 最大堆(Max Heap):每个节点的值都大于或等于其子节点的值。根节点是最大值。
- 最小堆(Min Heap):每个节点的值都小于或等于其子节点的值。根节点是最小值。
堆的基本操作
-
插入(Insert):
- 将新元素添加到堆的末尾。
- 通过“上浮”操作(Bubble Up)调整堆的结构,确保堆性质得以保持。
-
删除(Delete):
- 通常删除堆顶元素(最大值或最小值)。
- 将堆顶元素替换为最后一个元素,然后通过“下沉”操作(Bubble Down)调整堆的结构。
-
堆化(Heapify):
- 将一个无序数组转换为堆结构。可以通过从最后一个非叶子节点开始,依次进行下沉操作来实现。
应用场景
- 优先队列:堆常用于实现优先队列,支持高效的插入和删除操作。
- 排序算法:堆排序(Heap Sort)是一种基于堆的排序算法,时间复杂度为 (\(O(n \log n)\))。
- 图算法:在 Dijkstra 和 Prim 算法中,堆用于高效地获取最小或最大权重的边。
总结
堆是一种高效的树形数据结构,适用于需要频繁插入和删除最大或最小元素的场景。其结构的完全性和堆性质使得许多操作能够在对数时间内完成。
二分图(Bipartite Graph)
二分图是一种特殊的图,其顶点可以分为两个不相交的集合,使得图中的每条边都连接来自不同集合的顶点。换句话说,二分图的顶点集可以被划分为两个部分,且图中没有边连接同一部分的顶点。
基本特性:
- 顶点划分:存在两个集合 ( U ) 和 ( V ),使得每条边连接的两个顶点分别来自 ( U ) 和 ( V )。
- 无奇环:二分图中不存在长度为奇数的环。
基本操作:
- 检查二分性(IsBipartite):通过图的遍历(如 BFS 或 DFS)来判断图是否为二分图。
- 构建二分图:根据给定的边集,将顶点分配到两个集合中。
特点:
- 颜色标记:可以用两种颜色标记顶点,确保相邻顶点颜色不同。
- 应用广泛:在匹配问题、网络流、社交网络分析等领域有重要应用。
应用场景:
- 匹配问题:如婚姻匹配、工作分配等。
- 社交网络:分析用户与兴趣之间的关系。
- 图着色:解决图的着色问题,确保相邻顶点不同色。
欧拉图(Eulerian Graph)
欧拉图是一种特殊的图,其中存在一条经过每条边恰好一次的闭合路径,称为欧拉回路。如果图中存在一条经过每条边恰好一次但不一定回到起点的路径,则称为欧拉路径。
基本特性:
- 欧拉回路:图中存在一条回路,经过每条边一次且仅一次。
- 欧拉路径:图中存在一条路径,经过每条边一次且仅一次,但不一定回到起点。
欧拉图的条件:
- 欧拉回路:图是连通的,且所有顶点的度数都是偶数。
- 欧拉路径:图是连通的,且恰好有两个顶点的度数为奇数,其余顶点的度数为偶数。
基本操作:
- 检查欧拉性(IsEulerian):判断图是否为欧拉图,检查顶点的度数和连通性。
- 构建欧拉回路/路径:使用 Fleury 算法或 Hierholzer 算法找到欧拉回路或路径。
特点:
- 连通性:欧拉图必须是连通的,确保可以从一个顶点到达另一个顶点。
- 边的使用:每条边只能使用一次,适用于需要遍历所有边的场景。
应用场景:
- 邮递员问题:寻找最短路径以遍历所有街道。
- 网络设计:优化网络连接,确保每条连接都被使用。
- 游戏设计:设计关卡或路径,确保玩家体验完整的游戏过程。
有向无环图(Directed Acyclic Graph, DAG)
有向无环图是一种特殊的图,其中所有边都有方向,并且不存在从某个顶点出发经过边回到自身的路径。
基本特性:
- 有向性:图中的边是有方向的,表示从一个顶点指向另一个顶点。
- 无环性:图中不存在环,即不可能从某个顶点出发经过边回到自身。
有向无环图的条件:
- 无环性:图中不包含任何环。
- 有向性:每条边都有明确的方向。
基本操作:
- 拓扑排序(Topological Sorting):对有向无环图进行排序,使得对于每一条边 (\(u \to v\)),顶点 (u) 在顶点 (v) 之前。
- 检测环(Cycle Detection):判断图是否为有向无环图,通常使用深度优先搜索(DFS)或 Kahn 算法。
特点:
- 层次结构:有向无环图常用于表示层次结构,如任务调度、依赖关系等。
- 唯一性:拓扑排序可能不唯一,存在多种有效的排序方式。
应用场景:
- 任务调度:表示任务之间的依赖关系,确保任务按顺序执行。
- 编译顺序:在编译过程中,处理源文件的依赖关系。
- 数据流分析:在计算机科学中,表示数据处理的顺序和依赖关系。
拓扑排序(Topological Sorting)
拓扑排序是对有向无环图(DAG)的一种线性排序,使得对于图中的每一条有向边 ( \(u \to v\) ),顶点 ( \(u\) ) 在排序中出现在顶点 ( \(v\) ) 之前。
基本特性:
- 唯一性:对于一个有向无环图,拓扑排序不一定是唯一的,可能存在多个有效的排序。
- 存在性:只有在图是有向无环图的情况下,才能进行拓扑排序。
拓扑排序的条件:
- 图必须是有向无环图(DAG)。
- 图中不能存在环路。
基本操作:
-
Kahn 算法:
- 计算每个顶点的入度。
- 将入度为 0 的顶点加入队列。
- 逐步移除队列中的顶点,并更新其邻接顶点的入度,直到所有顶点都被处理。
-
深度优先搜索(DFS):
- 对每个未访问的顶点进行 DFS。
- 在回溯时,将顶点加入栈中。
- 最终从栈中弹出顶点,得到拓扑排序。
特点:
- 线性时间复杂度:拓扑排序的时间复杂度为 ( \(O(V + E)\) ),其中 ( \(V\) ) 是顶点数,( \(E\) ) 是边数。
- 适用性:广泛应用于任务调度、编译顺序、依赖关系管理等场景。
应用场景:
- 任务调度:在有依赖关系的任务中,确定执行顺序。
- 编译顺序:在编译多个源文件时,确保依赖关系得到满足。
- 课程安排:在学术课程中,确保 prerequisite 课程在后续课程之前完成。
哈希表(Hash Table)
哈希表是一种数据结构,通过哈希函数将键映射到数组的索引,以实现快速的数据存取。它支持高效的插入、删除和查找操作。
基本特性:
- 键值对存储:哈希表以键值对的形式存储数据,每个键唯一对应一个值。
- 快速访问:通过哈希函数,能够在平均常数时间复杂度 (O(1)) 内访问元素。
哈希函数:
- 定义:将输入(键)转换为数组索引的函数。
- 要求:应尽量均匀分布,以减少冲突。
冲突处理:
- 链式法:在同一索引处使用链表存储多个元素。
- 开放地址法:在发生冲突时,寻找下一个可用的索引。
基本操作:
- 插入(Insert):计算键的哈希值,将键值对存入相应索引。
- 查找(Search):计算键的哈希值,查找对应的值。
- 删除(Delete):计算键的哈希值,移除对应的键值对。
特点:
- 动态扩展:当负载因子(已存储元素与数组大小的比率)过高时,可以扩展数组大小并重新哈希。
- 空间效率:相较于其他数据结构,哈希表在存储和访问上通常更高效。
应用场景:
-
数据库索引:快速查找记录。
-
缓存实现:存储临时数据以提高访问速度。
-
唯一性检查:快速判断元素是否存在于集合中。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号