P1600 天天爱跑步题解
P1600 天天爱跑步 [题解]
题目简述
在一棵树上,有 \(m\) 个玩家同时出发,第 \(i\) 个玩家的起点为 \(s_i\),终点为 \(t_i\) ,每秒走一条边 。每个节点上有一个观察员,一个玩家在第 \(w_j\) 秒正好到达了结点 \(j\) 会被观察到,问每个观察员会观察到多少人。
- 样例输入 #1
6 3 //n m
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3 //w[i]
1 5
1 3
2 6
- 样例输出 #1
2 0 0 1 1 1
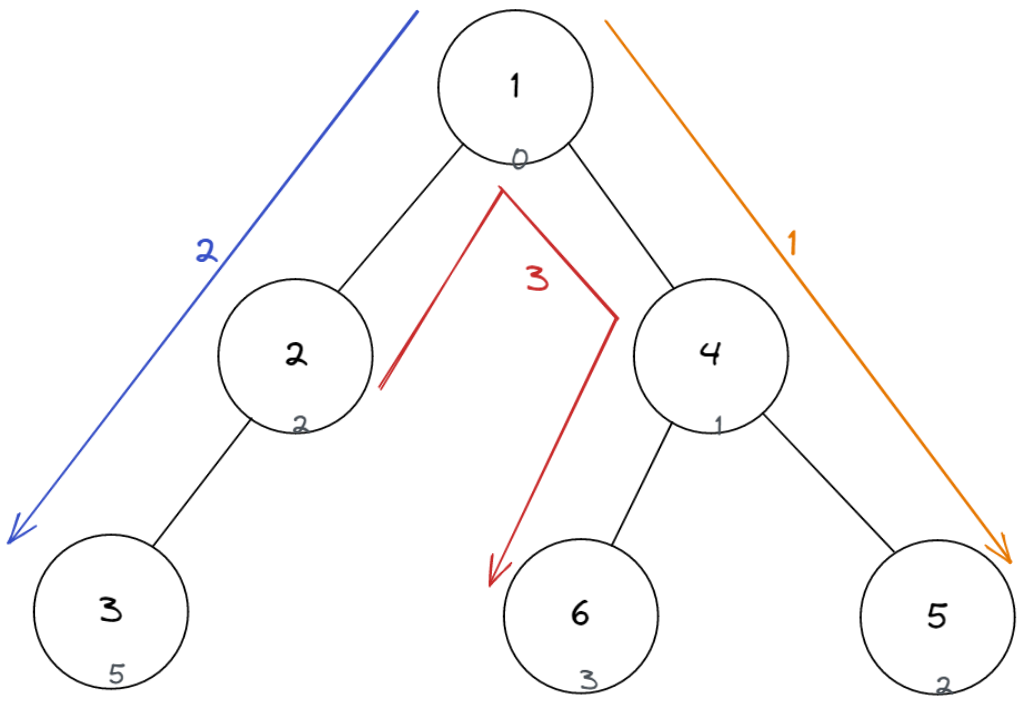
分析
-
考虑模拟每一个玩家走的路线,判断路线上的每一个点是否能被观察到,超时。
-
考虑从每一个观察员出发,逆向寻找能被观察到的玩家,如果每一个观察员都搜索一遍,超时。
-
观察数据范围,我们要在 \(O(n)\) 的时间复杂度内解决问题,也就是说只能对这棵树进行一次搜索。
-
我们发现,如果一个玩家能被观察到,那他的起点或终点一定在这个观察员的子树之中,这为我们的一次搜索提供了有利条件。
-
根据上一条分析,我们分情况讨论。
- 起点在观察员的子树之中。
- 终点在观察员的子树之中。
- 考虑一种特殊情况:起点和终点都在观察员的子树之中,那么观察员一定是起点和终点的 \(LCA\) 。我们需要对这种情况进行特殊处理,否则这条路径将会被计算两次。
下图对应上述三种情况 (看不清请点击:.PNG)。其中,\(d[i]\) 代表节点深度, \(w[i]\) 同题目(一个玩家在第 \(w_j\) 秒正好到达了结点 \(j\) 会被观察到),\(dis\) 代表 \(start\) 与 \(end\) 之间的距离。
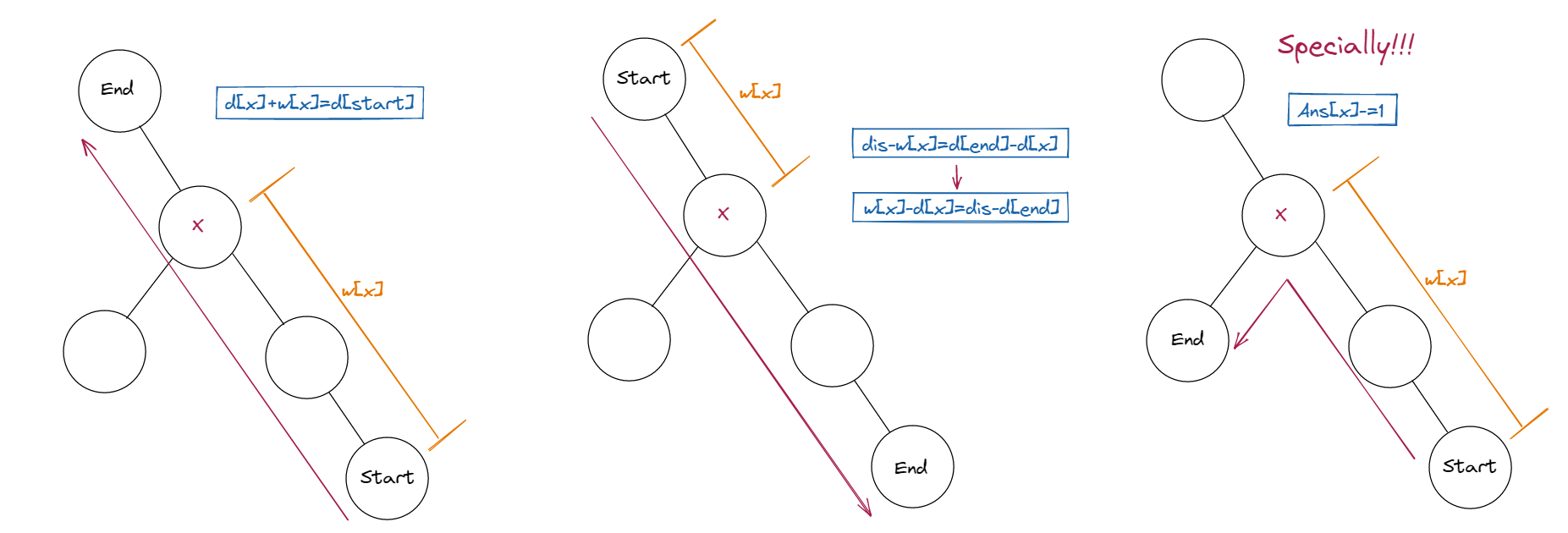
-
所以,当我们来到一个节点 \(x\) 时,我们只需要知道它的子树中有多少节点满足以上条件即可。(\(k\) 节点在 \(x\) 的子树中,当 \(d[x]+w[x]=d[k]\) 且 \(w[x]-d[x]=dis-d[k]\) 时, \(k\) 会被 \(x\) 观察到)
-
我们提前记录每个点(\(k\)节点)的 \(d[k]\) , \(dis-d[k]\) 。这样,当我们回溯时,只需要用前辈节点(\(x\)节点)的\(d[x]+w[x]\) , \(w[x]-d[x]\) 与之进行比较,就可得知哪些节点能被 \(x\) 节点观察到。
-
利用桶的思想,实现记录上述两个值(\(d[k]\) , \(dis-d[k]\) )。此处以 \(d[k]\) 来举例,定义桶数组 \(bucket[]\) ,对于每一个节点 \(k\) ,\(bucket[d[k]]++\) ,回溯到它们的先辈节点时,只需要访问 \(bucket[d[x]+w[x]]\) ,便可得知能被观察到的子节点的数量。
代码实现
- 完整代码(无注释,下方有详细的解释)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=300000,LG=20;
int n,m,tot=0,head[N],w[N],fa[N][LG+1],d[N];
int bu1[N],bu2[N*2+1000],cnt_st[N],ans[N],dis[N],s[N],t[N];
int tot1=0,tot2=0,head1[N],head2[N];
struct node
{
int next,to;
}e[N*2],e1[N*2],e2[N*2];
void add(int x,int y)
{
e[++tot].next=head[x];
e[tot].to=y;
head[x]=tot;
}
void add1(int x,int y)
{
e1[++tot1].next=head1[x];
e1[tot1].to=y;
head1[x]=tot1;
}
void add2(int x,int y)
{
e2[++tot2].next=head2[x];
e2[tot2].to=y;
head2[x]=tot2;
}
void dfs(int x,int f,int dep)
{
fa[x][0]=f,d[x]=dep;
for(int i=1;(1<<i)<=d[x];i++)fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(v!=f)dfs(v,x,dep+1);
}
}
int lca(int x,int y)
{
if(d[x]<d[y])swap(x,y);
for(int i=LG;i>=0;i--)
if(d[x]-(1<<i)>=d[y]) x=fa[x][i];
if(x==y)return x;
for(int i=LG;i>=0;i--)
{
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
}
return fa[x][0];
}
void dfs2(int x,int f)
{
int bu1_save=bu1[d[x]+w[x]],bu2_save=bu2[w[x]-d[x]+N];
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].to;
if(v!=f)
{
dfs2(v,x);
}
}
bu1[d[x]]+=cnt_st[x];
for(int i=head1[x];i;i=e1[i].next)
{
int v=e1[i].to;
bu2[dis[v]-d[x]+N]++;
}
ans[x]+=bu1[d[x]+w[x]]-bu1_save+bu2[w[x]-d[x]+N]-bu2_save;
for(int i=head2[x];i;i=e2[i].next)
{
int v=e2[i].to;
bu1[d[s[v]]]--;
bu2[dis[v]-d[t[v]]+N]--;
}
}
signed main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n-1;i++)
{
int x,y;
scanf("%lld%lld",&x,&y);
add(x,y),add(y,x);
}
dfs(1,1,0);
for(int i=1;i<=n;i++)cin>>w[i];
for(int i=1;i<=m;i++)
{
scanf("%lld%lld",&s[i],&t[i]);
int o=lca(s[i],t[i]);
add1(t[i],i);
add2(o,i);
cnt_st[s[i]]++;
dis[i]=d[s[i]]+d[t[i]]-2*d[o];
if(d[o]+w[o]==d[s[i]])ans[o]--;
}
dfs2(1,1);
for(int i=1;i<=n;i++)printf("%lld ",ans[i]);
return 0;
}
- 代码解释
- \(fa[i][lg]\) 为倍增法中的父亲数组,存储节点 \(i\) 向上的第 \(2^{lg}\) 个父亲,用于高效地查询 \(lca\)。
- \(cnt\_st[0]\) 存储以当前节点为起点的路径的数量,具体使用见后文。
- \(bu1[],bu2[]\) 分别是上行、下行的桶, \(bu1[]\) 在前文已解释(即 \(bucket[]\)),\(bu2[]\) 比较特殊,\(w[x]-d[x]\) (或 \(dis[v]-d[x]\))作为下标可能为负数,所以要加上一个 \(N\) 作为偏移量,防止溢出。
- \(e[],e1[],e2[]\) 为三个链式前向星,其中 \(e[]\) 用于存储题目中的树形地图,\(e1[],e2[]\) 则是用于存储以当前节点为 \(end\) 或 \(lca\) 的所有路径的编号(具体原因见后文),这是一种取巧的方法,当然也可以用 \(vector\) 来存储。
- \(dfs()\) 用于初始化 \(fa[][]\) 数组,用于之后的 \(lca()\) 计算。
- \(dfs2()\) 为核心代码。
- 搜索整颗树的过程中,维护 \(bu1[],bu2[]\) 两个桶,从而计算做出贡献的子节点的数量。而 \(bu1\_save,bu2\_save\) 则用来存储访问子树前的桶内数值,从而计算访问子树前后桶内数值的差,也就是所有子节点所作的贡献。
- 第一个循环用于访问子树。
bu1[d[x]]+=cnt_st[x];为装桶过程,存储的是深度为 \(d[x]\) 的起点的数量。- 第二个循环,将终点入桶。因为需要用到 \(dis[]\) 参数,其下标为路径编号,而单一的数组只能存储节点的数量(如 \(cnt\_st\) ),所以要使用前向星(或 \(vector\) )来存储每个终点对应的路径编号。
- 此时访问子树的任务已经完成,于是计算当前节点答案,计算差值的原因前文已说明。需要注意的是,因为符合条件的终点和观察员可能重合,所以此步骤不能在第二个循环之前。
- 第三个循环,处理当前节点为 \(lca\) 的情况。容易发现,树上两个点一定比它们的 \(lca\) 更深(其中一个点可能与 \(lca\) 重合),这两个点就不会经过比 \(lca\) 更浅的点了,所以要减去它们在桶中的值。
- 主函数中有一行
if(d[o]+w[o]==d[s[i]])ans[o]--;便是用来处理前文所说的特殊情况,因为这个点要被计算两次,所以答案提前减一就行了。
其他
洛谷原题:https://www.luogu.com.cn/problem/P1600 。
博客:https://www.cnblogs.com/tommyjin/articles/18415033 。
洛谷专栏:https://www.luogu.com.cn/article/h2nvb8ow 。
演示图片(.PNG):https://cdn.luogu.com.cn/upload/image_hosting/2pkuqdnl.png 。
演示图片(.SVG):http://218.201.91.220:8989/s/K3x2EZT...。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号