Loading

[2024-07-18]P5303 逼死强迫症

P5303 逼死强迫症

题目描述

用足够多的 \(2*1\) 的方块和两个 \(1*1\) 的方块填满 \(2*N\) 的矩形，但是两个 \(1*1\) 的方块不能相邻，问有多少种方案。

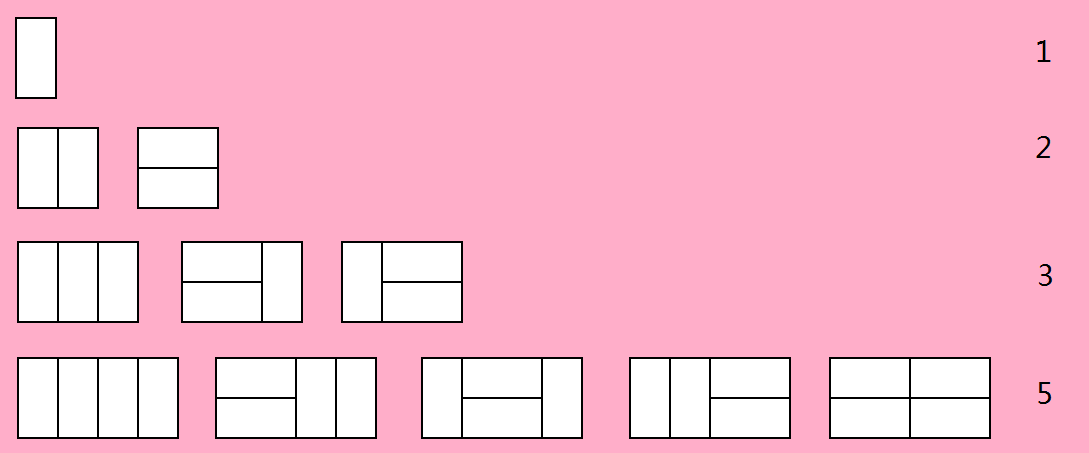
比如 \(N=4\) 共有6中方案，解释如下：

img

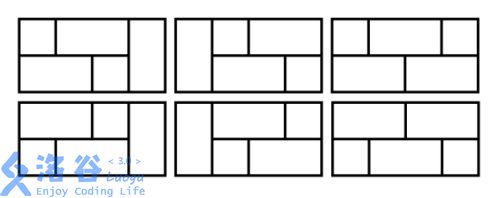
分析

  • 很明显要推导出递推式，那么我们定义 \(f[i]\) 为 \(N=i\) 时的方案数量。

  1. 在 \(f[i-1]\) 的矩形的右边竖着放置一个 \(1*2\) 的方块，则 \(f[i]+=f[i-1]\) 。

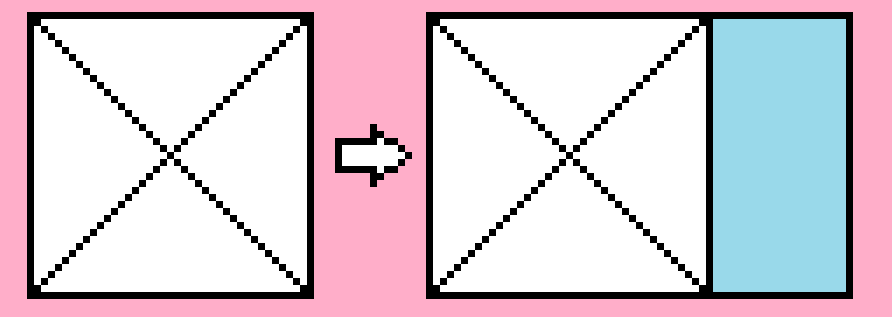
  2. 在 \(f[i-2]\) 的矩形的右边横着放置两个 \(2*2\) 的方块，则 \(f[i]+=f[i-2]\) 。

  3. 当添加的一行填有 \(1*1\) 的方块（这里讨论 \(1*1\) 的方块在右上角，右下角同理）。

    • 由于 \(1*1\) 方块上下不能与另一个 \(1*1\) 方块相邻，所以这三个方块是固定的。

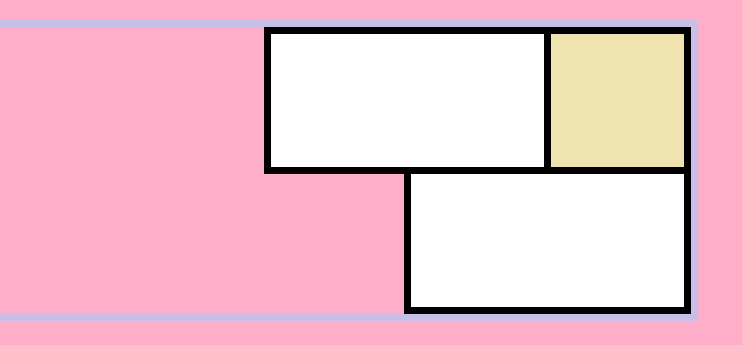
    • 另一个 \(1*1\) 方块（称作小蓝）可以放在下方或上方，我们发现对于每一个位置，小蓝右边区域的放置方案是固定的，小蓝左边区域只需要使用 \(1*2\) 的方块进行填充。

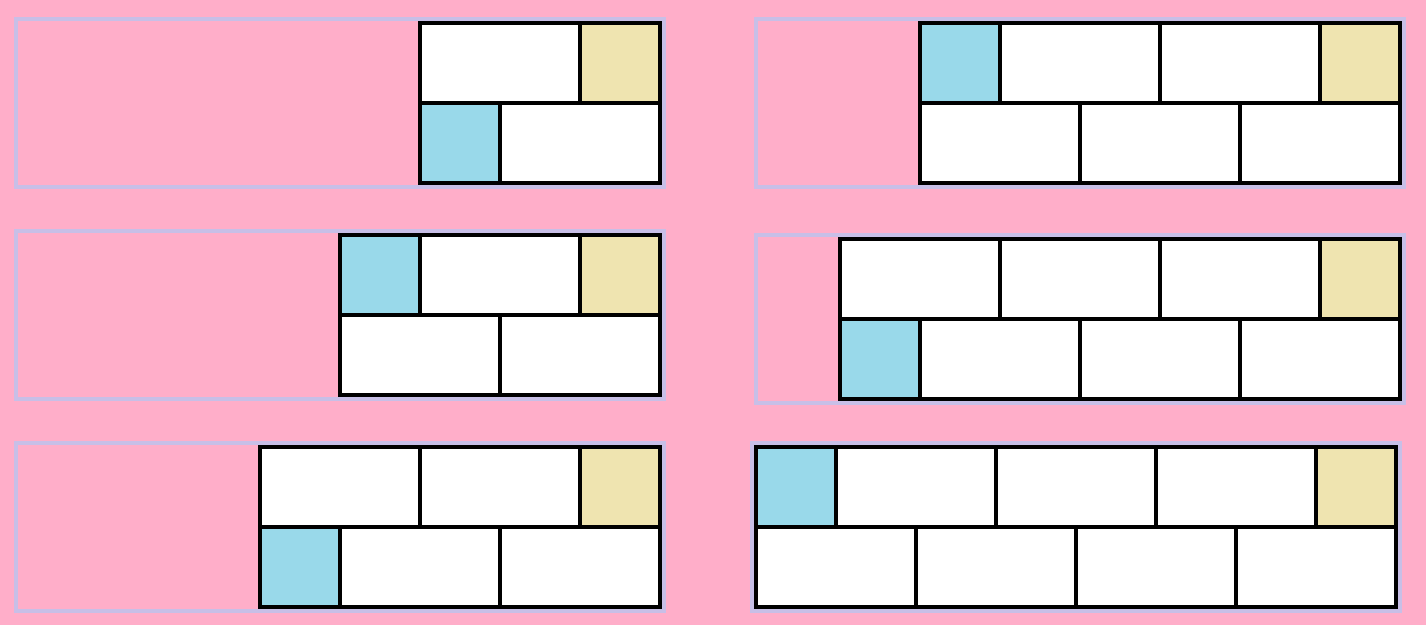
    • 对于每一个 \(0<=k<=i-3\) 值计算方案数，此处定义 \(p[k]\) 为 \(2*k\) 的矩形中填充 \(1*2\) 方块的方案数。则 \(f[i]+=2*\sum\limits_{k=0}^{i-3}p[k]\) 。

    • 可以发现 \(p[k]=p[k-1]+p[k-2]\) ，即斐波那契额数列。

    • 斐波那契数列的前缀和满足 \(sum[n]=p[n+2]-1\) ，证明如下

      \(sum[n]=p[1]+p[2]+p[3]+...+p[n]\)

      \(sum[n]=1+p[1]+p[2]+p[3]+...+p[n]-1\)

      \(\because p[2]=1\)

      \(\therefore sum[n]=(p[2]+p[1])+p[2]+p[3]+...+p[n]-1\)

      \(sum[n]=(p[3]+p[2])+p[3]+...+p[n]-1\)

      \(sum[n]=(p[n]+p[n-1])+p[n]-1\)

      \(sum[n]=p[n+2]-1\)

    • 所以 \(2*\sum\limits_{k=0}^{i-3}p[k]=2*sum[i-3]=2*p[i-1]-2\) 。

  4. 综上，我们得到的递推式是\(f[i]=f[i-1]+f[i-2]+2*p[i-1]-2\) ，观察数据范围，暴力递推是不现实的，所以需要使用矩阵幂进行维护。

  5. 我们要求一个矩阵 \(S\) ，使得：\(\begin{bmatrix} f[i-1] & f[i-2] & p[i-1] & p[i-2] & 1 \end{bmatrix}*S=\begin{bmatrix} f[i] & f[i-1] & p[i]& p[i-1] & 1 \end{bmatrix}\) 。

    得到：\(S=\begin{bmatrix} 1 & 1 & 0 & 0 & \\ 1 & 0 & 0 & 0 & \\ 2 & 0 & 1 & 0 & \\ 0 & 0 & 1 & 0 & \\ -2 & 0 & 0 & 1 & \end{bmatrix}\) ，读者可以带入尝试。

  6. 由此可以推导出：\(\begin{bmatrix} f[2] & f[1] & p[2] & p[1] & 1 \end{bmatrix}*S^{n-1}=\begin{bmatrix} f[n+1] & f[n] & p[n+1] & p[n] & 1 \end{bmatrix}\) ，答案便是得到矩阵的第一行第二列。

  7. 使用矩阵快速幂求得 \(S^{n-1}\) 。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=10,p=1e9+7;
int t;
struct matrix
{
	int m[N][N];
}a,s,ans;
matrix operator * (const matrix& x,const matrix& y)	//重载矩阵乘法
{
	matrix c;
	memset(c.m,0,sizeof(c.m));
	for(int i=1;i<N;i++)
		for(int j=1;j<N;j++)
			for(int k=1;k<N;k++)
				c.m[i][j]=(c.m[i][j]+x.m[i][k]*y.m[k][j])%p;
	return c;
}
matrix pow_matrix(matrix x,int k)					//矩阵快速幂
{
	matrix c;
	memset(c.m,0,sizeof(c.m));
	for(int i=1;i<N;i++)c.m[i][i]=1;
	while(k)
	{
		if(k&1)c=c*x;
		k>>=1;
		x=x*x;
	}
	return c;
}
signed main()
{
	cin>>t;
	while(t--)
	{
		int n;
		cin>>n;
		a.m[1][1]=0,a.m[1][2]=0,a.m[1][3]=2,a.m[1][4]=1,a.m[1][5]=1;
		s.m[1][1]=1,s.m[1][2]=1,s.m[2][1]=1;
		s.m[3][1]=2,s.m[3][3]=1,s.m[3][4]=1;
		s.m[4][3]=1,s.m[5][1]=p-2,s.m[5][5]=1;		
		ans=a*pow_matrix(s,n-1);
		cout<<ans.m[1][2]<<endl;
	}
	
	return 0;
}

其他

posted @ 2024-09-15 10:26  TommyJin  阅读(22)  评论(0)    收藏  举报