完全背包问题

完全背包问题

思路：

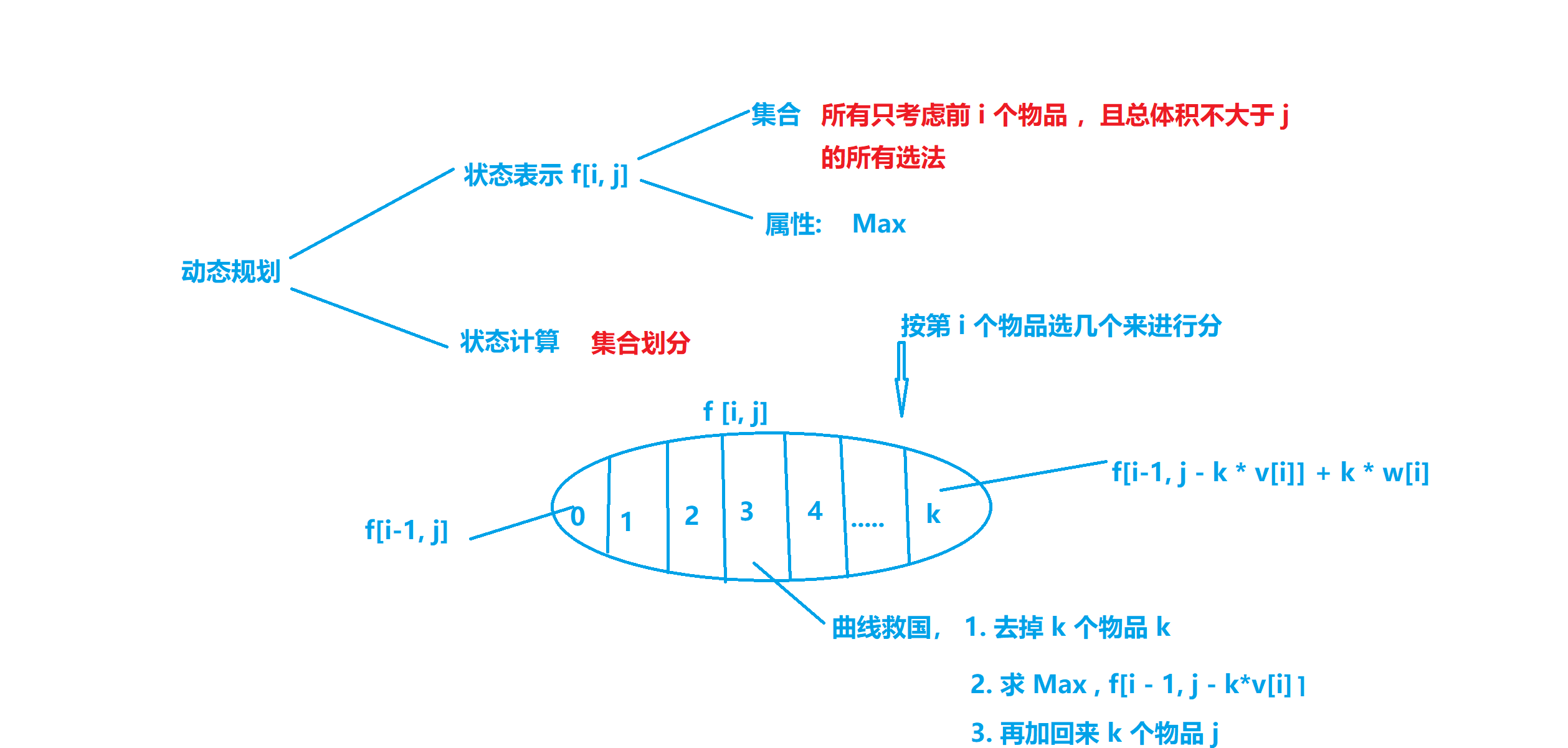
f[i][j] = f[i-1][j - k*v[i]] + k * w[i]

朴素版的做法

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin>>n>>m;
    
    for(int i = 1; i<=n; i++) cin>>v[i]>>w[i]; //输入每件物品的体积和价值
    
    for(int i = 1; i<=n; i++) //前i 个物品 ，总体积不超过 j 的最大价值
        for(int j = 0; j<=m; j++)
            for(int k = 0; k*v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
                
    cout<<f[n][m]<<endl;
    
    return 0;
}

**这个时间复杂度比较高，有的情况没办法 AC **

优化思路

我们列举一下更新次序的内部关系：

f[i, j] = max(f[i-1, j] , f[i - 1, j - v] + w , f[i-1, j - 2*v] + 2*w ,........ )
f[i,j - v] = max(          f[i-1, j - v]      ,  f[i-1, j - 2*v] + w ,......... )
由上两式，可以得出以下地推关系：
    			f[i][j] = max(f[i, j-v] + w, f[i-1][j])

有了上面的关系， 其实 k 循环可以不要了， 核心代码优化成这样

for(int i = 1; i <= n; i++)
    	for(int j = 0; j <= m; j ++)
        {
            f[i][j] = f[i-1][j];
            if(j - v[i] >= 0)
                	f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }

这个代码和 01 背包的非优化写法很像！！！， 我们对比一下， 下面是 01 背包的核心代码

for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= m ; j ++)
{
    f[i][j] = f[i-1][j];
    if(j-v[i]>=0)
        f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}

两个代码其实只有一句不同（注意下标）

f[i][j] = max(f[i][j] , f[i-1][j - v[i]] + w[i]); //01背包

f[i][j] = max(f[i][j] , f[i][j - v[i]] + w[i]); //完全背包问题

因为0和1背包问题很像， 我们很容易想到进一步优化， 核心代码可以改成这样

for(int i = 1; i <= n; i++)
    for(int j = v[i]; j<=m; j++)//注意了，这里的j是从小到大枚举， 和 01 背包不一样
    {
        f[j]  = max(f[j], f[j - v[i]] +w[i]);
    }

综上所述

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout<< f[m] << endl;

    return 0;
}