【高等数学笔记-极限(2)】函数的极限
引例
数列(无穷数列)本质上可以理解为的函数,即定义域为 N + \mathbb{N^+} N+的离散型特殊函数;
那么可以将数列的极限推广到函数的极限;
首先要解决在何处存在极限,对于数列来说,由于自变量仅存在一个 n n n,并且取值一定是 n → ∞ n \to \infty n→∞的;但是函数不一定;
首先实数系统中讨论:
极限值 a a a必须是确定的实数,即有限实数,即 a ∈ R a\in \mathbb{R} a∈R,极限值不可以为 ∞ \infty ∞;
-
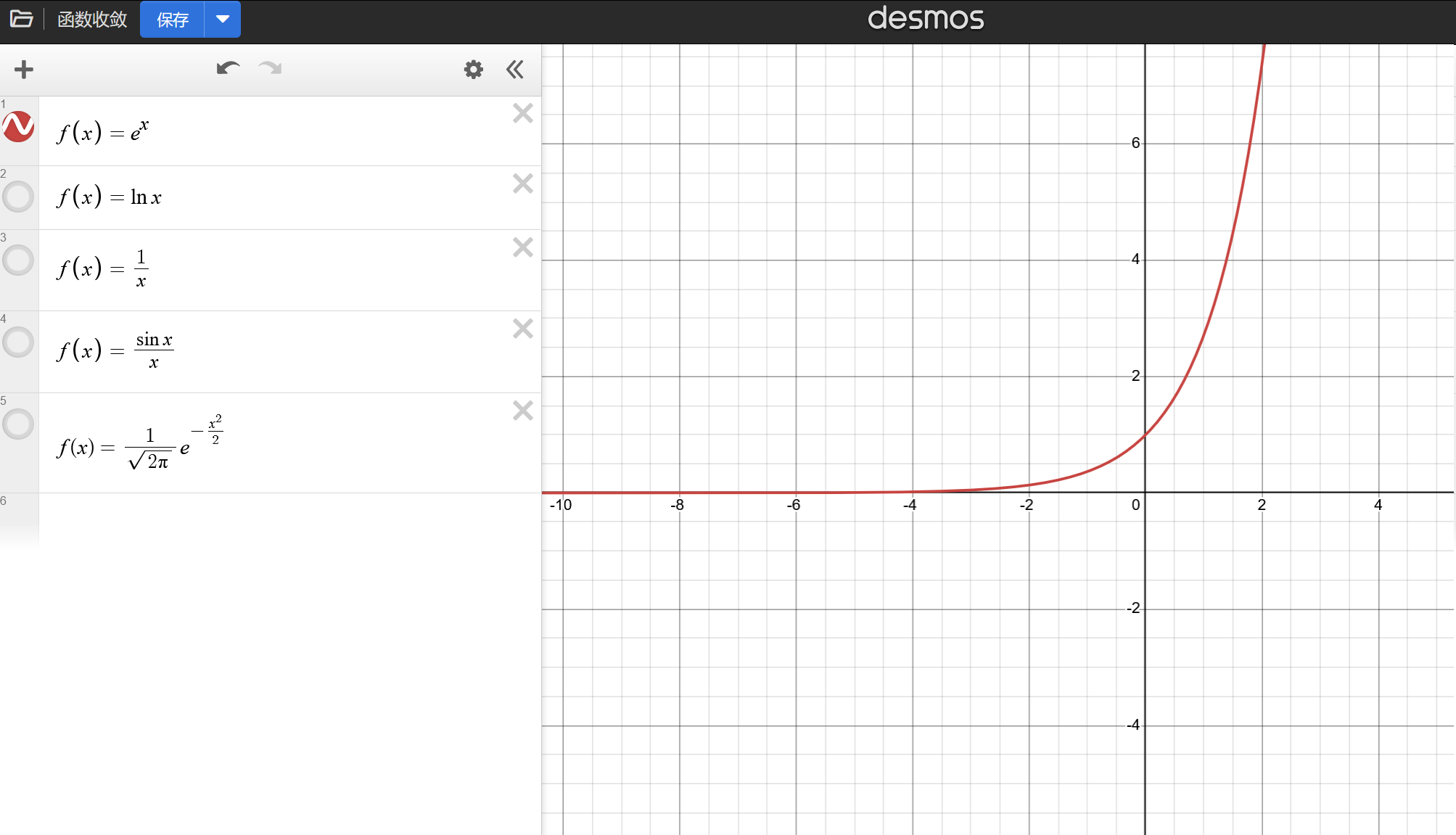
观察函数 f ( x ) = e x f(x)=e^x f(x)=ex的图像,显然在 n → − ∞ n \to -\infty n→−∞处收敛于 0 0 0
![在这里插入图片描述]()
-
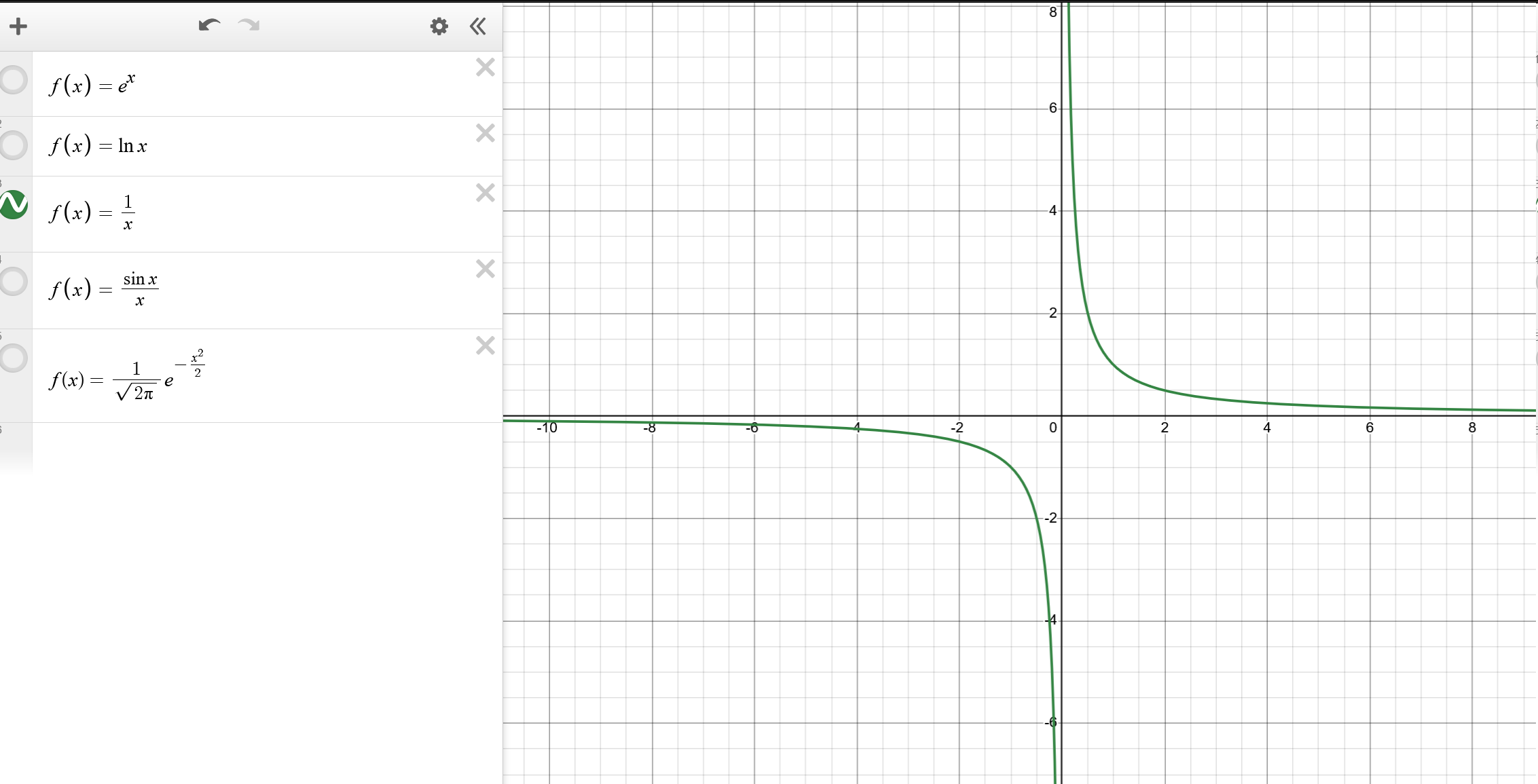
观察函数 f ( x ) = 1 x f(x)=\frac{1}{x} f(x)=x1的图像,显然存在2个极限,分别在 n → + ∞ n \to +\infty n→+∞和 n → − ∞ n \to -\infty n→−∞处均收敛于 0 0 0
![在这里插入图片描述]()
-
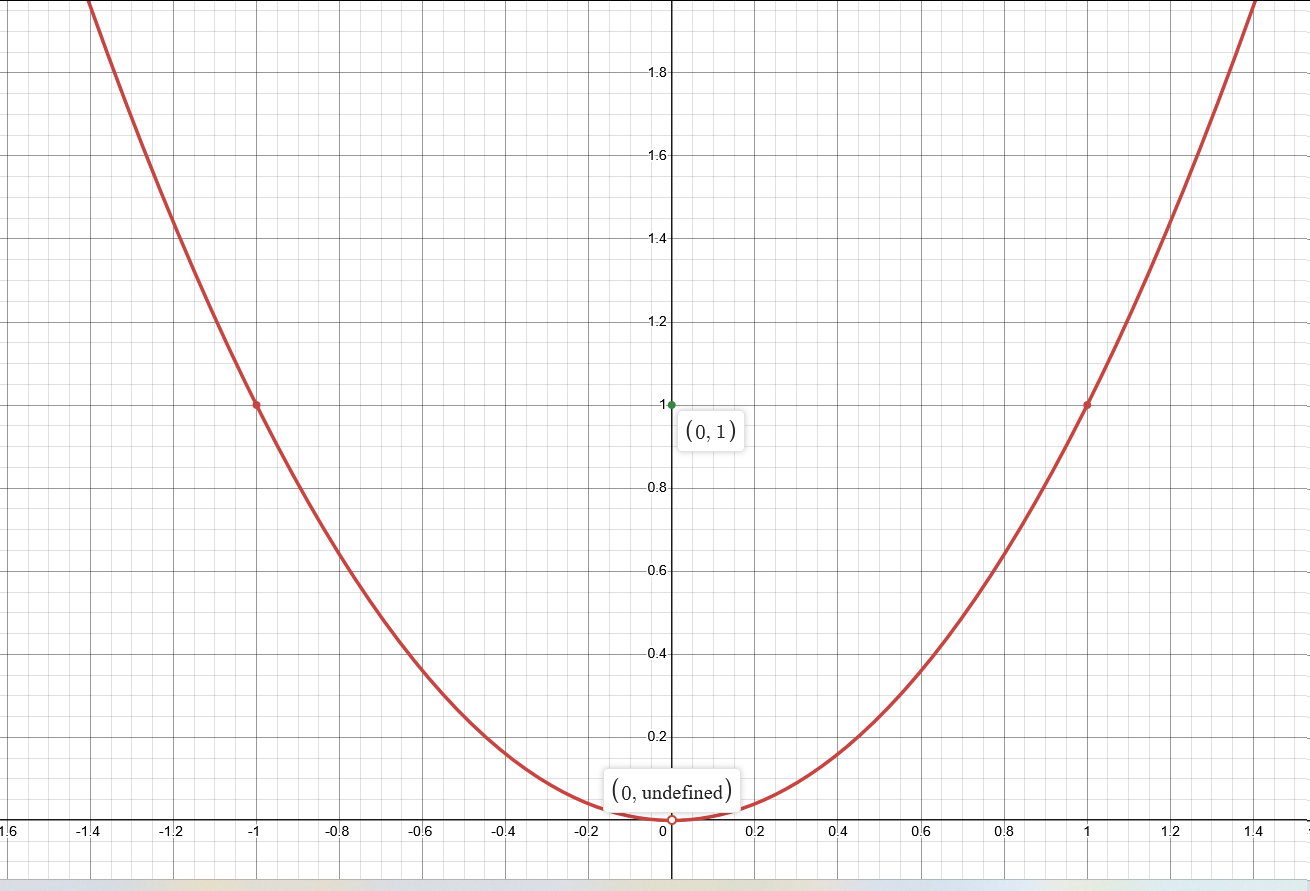
观察这个特殊的分段函数
f ( x ) = { x 2 , x ≠ 0 1 , x = 0 f(x)=\begin{cases} x^2,\quad x\ne0\\ 1,\quad x= 0\end{cases} f(x)={ x2,x=01,x=0
那么在0处的极限值应该是0还是1呢?
![在这里插入图片描述]()
-
更多请点击查看链接: 函数收敛示例
-
情况1,函数在 + ∞ +\infty +∞或 − ∞ -\infty −∞处有极限;即函数在 x → ∞ x\to \infty x→∞时的极限
-
情况2,函数在某点例如 x 0 x_0 x0处有极限;
- 函数在 x 0 x_0 x0处有定义
- 函数连续,函数值本身就是极限值:
- 函数在 x 0 x_0 x0处断开了,但是左右都是连续的
- 函数在 x 0 x_0 x0处无定义,函数两边的值都无限接近极限值,但是无法相等:
- 综上,核心是讨论:函数在 x 0 x_0 x0 附近的趋近行为,与函数是否在 x 0 x_0 x0处是否有定义无关,
- 函数在 x 0 x_0 x0处有定义
函数在某点 x 0 x_0 x0处有极限
定义
之前讨论过,常数列的极限是是常数本身;实际讨论函数在 x 0 x_0 x0处的极限,就是讨论在这个位置上,函数应该接近/等于何值?
- 首先相等是最接近的,如果函数连续,那么可以确定 x 0 x_0 x0在此处对应的函数值 f ( x 0 ) f(x_0) f(x0)的值(等同于在 x 0 x_0 x0上有定义),那么相等了,那么这个值就一定是极限;
- 如果函数在 x 0 x_0 x0上没有定义,但是函数在 x 0 + δ x_0+\delta x0+δ和 x 0 − δ {x_0-\delta} x0−δ上有定义, 那么在 δ → 0 \delta \to 0 δ→0的过程中, f ( x 0 + δ ) f(x_0+\delta) f(x0+δ)和 f ( x 0 − δ ) f(x_0-\delta) f(x0−δ)都接近了一个有限的确定的实数 a a a,那么 a a a也应该是他的极限;
- 如果函数在 x 0 x_0 x0上有定义,但是函数在 x 0 x_0 x0处断开了,就应该视作2的情况来讨论;
类比数列的极限定义可以很容易写出函数的极限的定义
数列极限定义
∀ ε > 0 , ∃ N > 0 ; 当 n > N 时 , 有 ∣ x n − a ∣ < ε \forall \varepsilon>0,\exists N>0;当n>N时,有|x_n-a|<\varepsilon ∀ε>0,∃N>0;当n>N时,有∣xn−a∣<ε
函数极限定义( x 0 x_0 x0处)
∀ ε > 0 , ∃ δ > 0 ; 当 0 < ∣ x − x 0 ∣ < δ 时 , 有 ∣ f ( x ) − a ∣ < ε \boxed{\forall \varepsilon>0,\exists \delta>0;当0<|x-x_0|<\delta时,有|f(x)-a|<\varepsilon} ∀ε>0,∃δ>0;当0<∣x−x0∣<δ时,有∣f(x)−a∣<ε
等同于
∀ ε > 0 , ∃ δ > 0 ; 当 0 < ∣ x − x 0 ∣ < δ 时 ⏟ ∀ x ∈ U ˚ ( x 0 , δ ) , 有 ∣ f ( x ) − a ∣ < ε \forall \varepsilon>0,\exists \delta>0;\underbrace{当0<|x-x_0|<\delta时}_{\forall x \in \r{U}(x_0,\delta)},有|f(x)-a|<\varepsilon ∀ε>0,∃δ>0;∀x∈U˚(x0,δ)
当0<∣x−x0∣<δ时,有∣f(x)−a∣<ε
实际 δ \delta δ至少是一个满足条件的最大距离,它可以更小,这个距离即 ∣ x 0 + δ ∣ |x_0+\delta| ∣x0+δ∣,只要它能满足;那么对于更小的距离 ∣ x − x 0 ∣ |x-x_0| ∣x−x0∣,那么一定能满足;
就和数列的 N N N一样,如果第 N N N项满足了,那么 N N N项往后的任意一项 n n n,都可以满足;
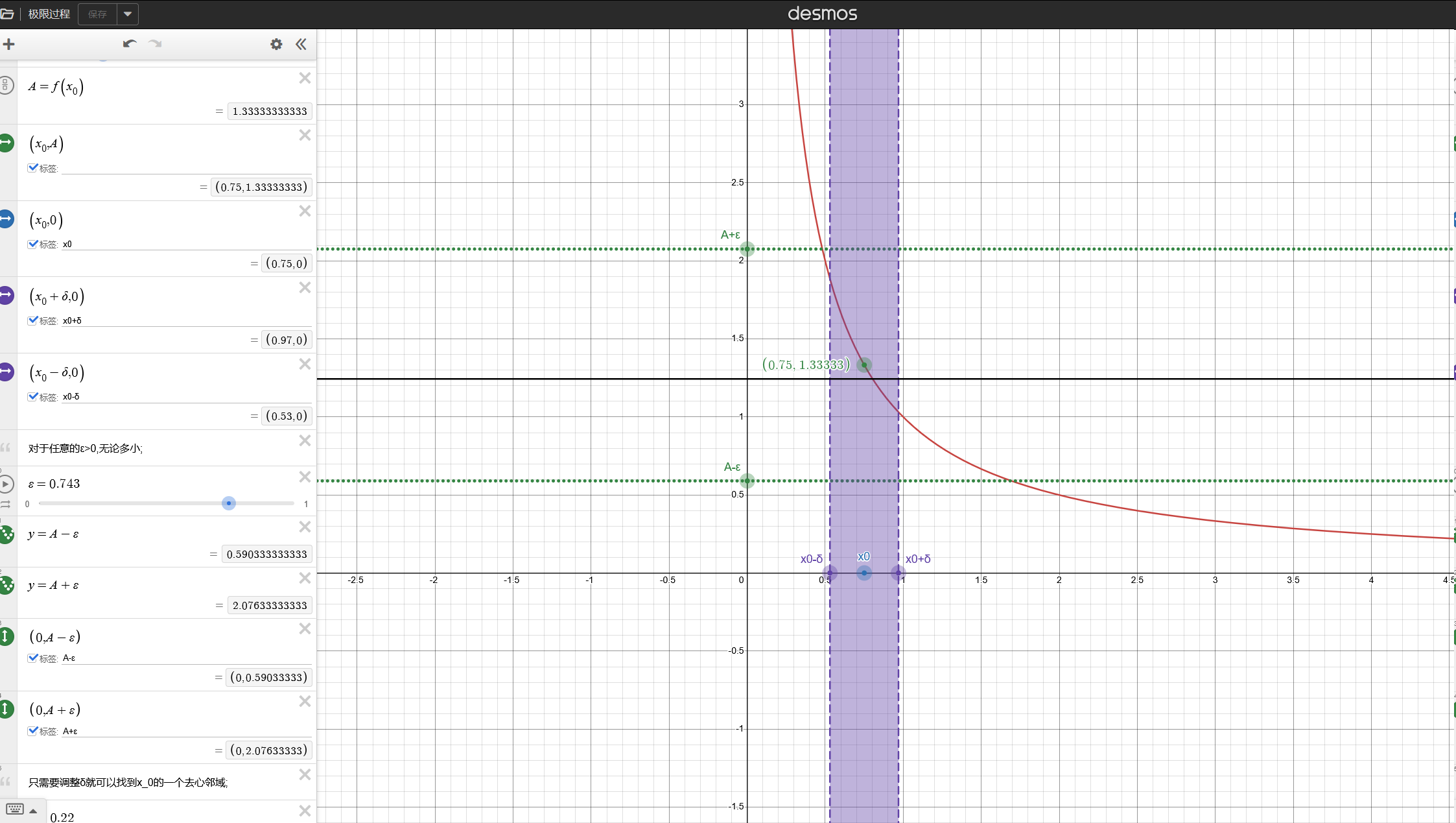
上图链接,调整 ε , δ \varepsilon,\delta ε,δ,操作试试:极限过程
在求证函数在 x 0 x_0 x0处的极限是A;
也就是寻找一个 U ˚ ( x 0 , δ ) \r{U}(x_0,\delta) U˚(x0,δ),使得属于这个邻域的任意一个数对应的函数值,落在 A ± ε A\pm \varepsilon A±ε内
严格单调且连续的函数 f ( x ) f(x) f(x),且反函数也连续时
若我将原函数的反函数记为 g ( x ) g(x) g(x),这个邻域最大范围实际就是 g ( A ± ε ) g(A\pm \varepsilon) g(A±ε)的范围
左右极限
示例
f ( x ) = { x , x ∈ ( − 2 , − 1 ) ∪ ( − 1 , 1 ] x + 1 , x ∈ ( 1 , 2 ) f(x)=\begin{cases} x,\quad x\in(-2,-1)\cup(-1,1]\\ x+1,\quad x\in(1,2) \end{cases} f(x)={
x,x∈(−2,−1)∪(−1,1]x+1,x∈(1,2)
绘制他的图像可见以下结论
| x x x | 左极限 | 右极限 | 极限 |
|---|---|---|---|
| -2 | x | √ | x |
| -1 | √ | √ | √ |
| 1 | √ | √ | x |
| 2 | √ | x | x |
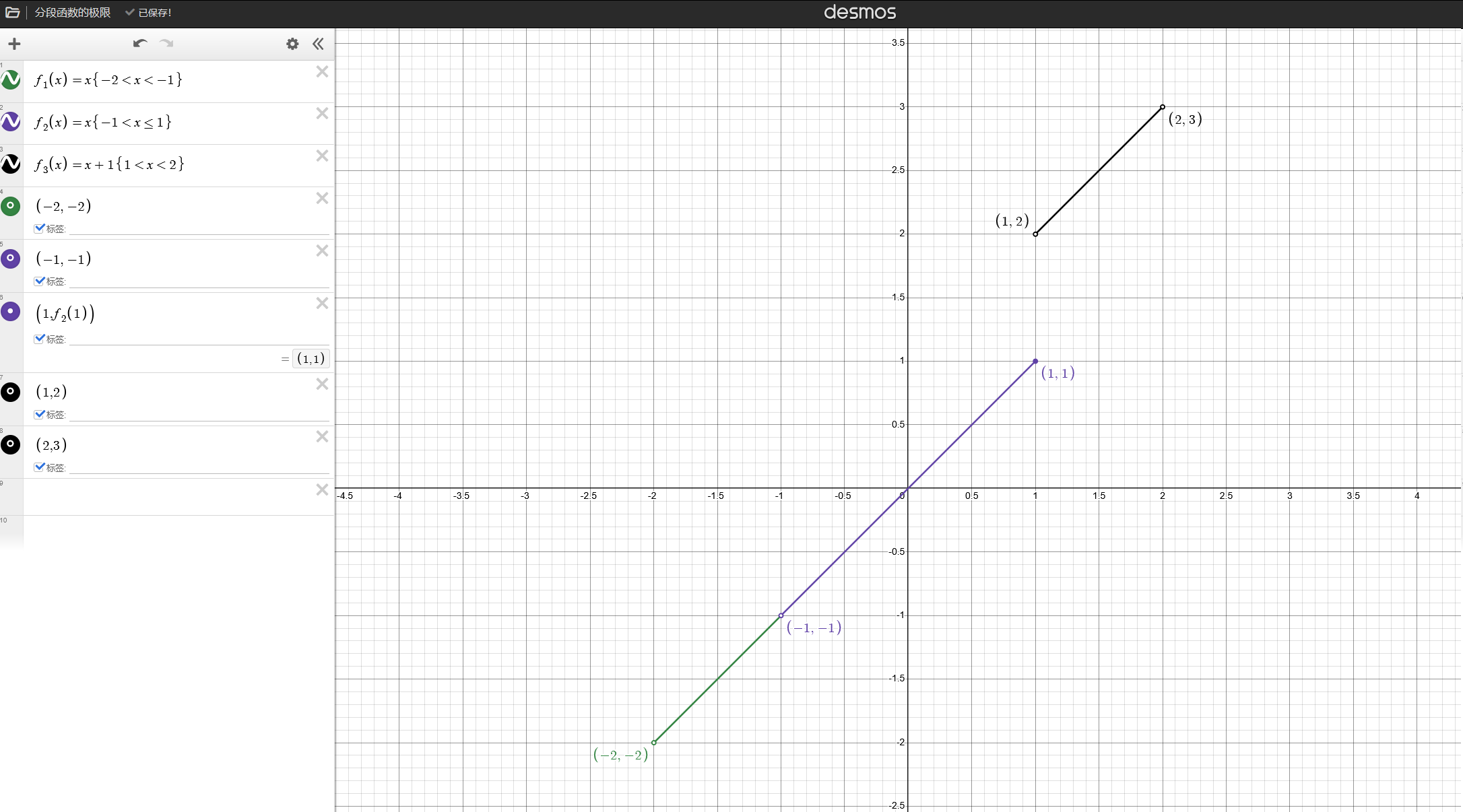
关键点分析
1. x = − 2 x = -2 x=−2
- 左极限:
函数在 x = − 2 x = -2 x=−2左侧未定义(定义域从 − 2 -2 −2开始),左极限不存在(记为x)。 - 右极限:
当 x → − 2 + x \to -2^+ x→−2+时, x ∈ ( − 2 , − 1 ) x \in (-2, -1) x∈(−2,−1), f ( x ) = x f(x) = x f(x)=x,故右极限为 − 2 -2 −2(记为√)。 - 极限:
因左极限不存在,整体极限不存在(记为x)。
2. x = − 1 x = -1 x=−1
- 左极限:
当 x → − 1 − x \to -1^- x→−1−时, x ∈ ( − 2 , − 1 ) x \in (-2, -1) x∈(−2,−1), f ( x ) = x f(x) = x f(x)=x,故左极限为 − 1 -1 −1(记为√)。 - 右极限:
当 x → − 1 + x \to -1^+ x→−1+时, x ∈ ( − 1 , 1 ] x \in (-1, 1] x∈(−1,1], f ( x ) = x f(x) = x f(x)=x,故右极限为 − 1 -1 −1(记为√)。 - 极限:
左右极限相等,极限存在且为 − 1 -1 −1(记为√)。
3. x = 1 x = 1 x=1
- 左极限:
当 x → 1 − x \to 1^- x→1−时, x ∈ ( − 1 , 1 ] x \in (-1, 1] x∈(−1,1], f ( x ) = x f(x) = x f(x)=x,故左极限为 1 1 1(记为√)。 - 右极限:
当 x → 1 + x \to 1^+ x→1+时, x ∈ ( 1 , 2 ) x \in (1, 2) x∈(1,2), f ( x ) = x + 1 f(x) = x+1 f(x)=x+1,故右极限为 2 2 2(记为√)。 - 极限:
左右极限不等,极限不存在(记为x)。
4. x = 2 x = 2 x=2
- 左极限:
当 x → 2 − x \to 2^- x→2−时, x ∈ ( 1 , 2 ) x \in (1, 2) x∈(1,2), f ( x ) = x + 1 f(x) = x+1 f(x)=x+1,故左极限为 3 3 3(记为√)。 - 右极限:
函数在 x = 2 x = 2 x=2右侧未定义(定义域到 2 2 2为止),右极限不存在(记为x)。 - 极限:
因右极限不存在,整体极限不存在(记为x)。
定义与关系
实际就是从单侧逼近目标点 x 0 x_0 x0的行为,定义为:
左极限:
lim x → x 0 + f ( x ) = A 或 f ( x 0 + ) = A \lim_{x\to x_0^+}f(x)=A\quad 或 \quad f(x_0^+)=A x→x0+limf(x)=A或f(x0+)=A
lim x → x 0 + f ( x ) = A ⟺ ∀ ε > 0 , ∃ δ > 0 , 当 x 0 − δ < x < x 0 + δ 时 , 有 ∣ f ( x ) − A ∣ < ε \boxed{\lim_{x\to x_0^+}f(x)=A \iff \forall \varepsilon>0,\exists \delta>0,当x_0-\delta<x<x_0+\delta时,有|f(x)-A|<\varepsilon} x→x0+limf(x)=A⟺∀ε>0,∃δ>0,当x0−δ<x<x0+δ时,有∣f(x)−A∣<ε
右极限
lim x → x 0 − f ( x ) = A 或 f ( x 0 − ) = A \lim_{x\to x_0^-}f(x)=A\quad 或 \quad f(x_0^-)=A x→x0−limf(x)=A或f(x0−)=A
lim x → x 0 − f ( x ) = A ⟺ ∀ ε > 0 , ∃ δ > 0 , 当 x 0 − δ < x < x 0 时 , 有 ∣ f ( x ) − A ∣ < ε \boxed{\lim_{x\to x_0^-}f(x)=A \iff \forall \varepsilon>0,\exists \delta>0,当x_0-\delta<x<x_0时,有|f(x)-A|<\varepsilon} x→x0−limf(x)=A⟺∀ε>0,∃δ>0,当x0−δ<x<x0时,有∣f(x)−A∣<ε
与极限关系
lim x → x 0 f ( x ) = A ⟺ lim x → x 0 − f ( x ) = lim x → x 0 + f ( x ) = A \boxed{\lim_{x \to x_0}f(x)=A\iff \lim_{x \to x_0^-}f(x)=\lim_{x\to{x_0}^+}f(x)=A} x→x



 浙公网安备 33010602011771号
浙公网安备 33010602011771号