【剑指Offer-10】I. 斐波那契数列

问题

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例

输入：n = 2
输出：1

输入：n = 5
输出：5

解答1：递归

class Solution {
public:
    int fib(int n) {
        if (n < 2) return n;
        return (fib(n - 1) + fib(n - 2)) % 1000000007;
    }
};

解答2：带记忆递归

class Solution {
public:
    int fib(int n) {
        if (memo[n]) return memo[n];
        if (n < 2) return n;
        memo[n] = (fib(n - 1) + fib(n - 2)) % 1000000007;
        return memo[n];
    }
private:
    int memo[101]{};
};

重点思路

由图可知，直接使用递归会产生很多重复计算。我们可以暂存这些数据，减少内存与时间的消耗。

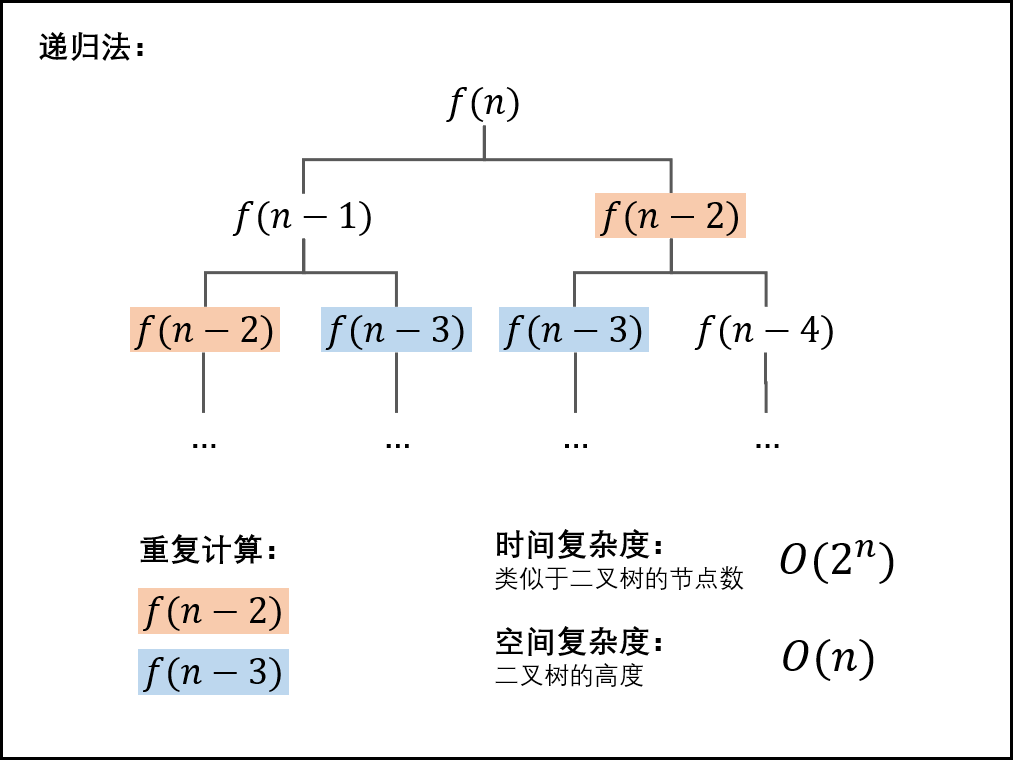
解答3：动态规划

class Solution {
public:
    int fib(int n) {
        if (n < 2) return n;
        int pre = 0, cur = 1;
        for (int i = 2; i <= n; i++) {
            int tmp = cur;
            cur = (pre + cur) % 1000000007;
            pre = tmp;
        }
        return cur;
    }
};

重点思路

状态转移方程已经写在题目里了，f(n) = f(n-1) + f(n-2)，注意边界条件即可。