【生成扩散模型】通过随机微分方程（SDE）构建 基于分数的生成建模

文章目录

• • 前言
  • 背景
  • • 基于朗之万动力学的去噪分数匹配(SMLD)
    • 去噪扩散概率模型(DDPM)
  • 使用SDE扰动数据
  • 通过反向随机微分方程生成样本
  • 评估SDE的分数
  • 示例: VE, VP SDES AND BEYOND
  • 结尾

前言

扩散模型的核心是加噪和去噪的过程通过离散的，但它依然属于随机过程的范畴，而就是，这一过程里数据随时间（或步骤）的随机变化能够看作一个随机过程。虽然实际中扩散模型的时间SDE 作为描述随机过程的通用工具，能为这类 “连续时间 + 随机扰动” 的演化提供严谨的数学表达 ——大部分随机过程都可视为 SDE 的解，这让它能精准刻画扩散模型中数据从真实分布到噪声分布，再从噪声分布逆推回真实分布的全过程。

背景

基于朗之万动力学的去噪分数匹配(SMLD)

参考文章：基于分数的生成模型SMLD（score-Matching） ------- Langevin Dynamics（朗之万动力学）公式推导

设 $p_{\sigma }(\tilde{x}|x):=\mathcal{N}(\tilde{x};x,{\sigma }^{2}I)$为扰动核（perturbation kernel），$p_{\sigma }(\tilde{x}):=\int p_{\text{data}}(x)p_{\sigma }(\tilde{x}|x)dx$为扰动后的边缘分布 —— 其中$p_{\text{data}}(x)$表示原始数据分布。

Perturbation kernel：扰动核 —— 用均值为 x、方差为${\sigma }^{2}I$的高斯分布，生成带噪声的扰动样本$\tilde{x}$。

乘以 $p_{\text{data}}(x)$ 是为了 “加权平均”—— 原始数据 x 本身有概率分布（有的 x 出现频繁，有的出现少），必须按原始数据的出现概率加权，才能得到所有扰动样本的整体分布。

考虑一组递增的正噪声尺度序列${\sigma }_{\text{min}}={\sigma }_1<{\sigma }_2<\cdots <{\sigma }_N={\sigma }_{\text{max}}$：

• ${\sigma }_{\text{min}}$足够小，使得$p_{{\sigma }_{\text{min}}}(x)\approx p_{\text{data}}(x)$（扰动微弱，接近原始数据分布）；
• ${\sigma }_{\text{max}}$足够大，使得$p_{{\sigma }_{\text{max}}}(x)\approx \mathcal{N}(x;0,{\sigma }_{\text{max}}^{2}I)$（扰动强烈，接近零均值高斯噪声分布）。

Song & Ermon (2019) 提出训练一个噪声条件分数网络（Noise Conditional Score Network, NCSN）$s_{\theta }(x,\sigma )$，其优化目标为去噪分数匹配（denoising score matching, Vincent, 2011）目标的加权和：

$${\theta }^{\star }=\arg \underset{\theta }{\min }\sum _{i=1}^N{\sigma }_i^2{\mathbb{E}}_{p_{\text{data}}(x)}{\mathbb{E}}_{p_{{\sigma }_i}(\tilde{x}|x)}\left[{\Vert s_{\theta }(\tilde{x},{\sigma }_i)-{\nabla }_{\tilde{x}}\log p_{{\sigma }_i}(\tilde{x}|x)\Vert }_2^2\right]（1）$$

• 网络 $s_{\theta }(\tilde{x},{\sigma }_i)$：输入是 “带噪声样本$\tilde{x}$” 和 “噪声尺度${\sigma }_i$”，输出是 “该样本在该尺度下的去噪方向”（分数函数近似）；
• 真实条件分数函数${\nabla }_{\tilde{x}}\log p_{{\sigma }_i}(\tilde{x}|x)$：“带噪声样本$\tilde{x}$要还原回原始数据 x 的最优方向”
• 权重 ${\sigma }_i^2$：给不同噪声尺度的训练分配权重，避免小噪声尺度（易学习）主导训练，确保大噪声尺度（难学习）也能充分训练；
• 双层期望 ${\mathbb{E}}_{p_{\text{data}}(x)}{\mathbb{E}}_{p_{{\sigma }_i}(\tilde{x}|x)}$：对 “所有原始数据” 和 “每个素材在该尺度下的所有可能噪声样本” 求平均，保证模型泛化性。

当数据量和模型容量足够时，最优基于分数的模型$s_{{\theta }^{\star }}(x,\sigma )$，在所有 $\sigma \in \{{\sigma }_i{\}}_{i=1}^N$下，几乎处处匹配目标分数函数${\nabla }_x\log p_{\sigma }(x)$。—— 即网络学会了 “在任意噪声强度下，如何判断带噪声样本的去噪方向”。

采样阶段，Song & Ermon (2019) 采用朗之万马尔可夫链蒙特卡洛（Langevin MCMC） 算法，对每个分布$p_{{\sigma }_i}(x)$依次执行 M 步迭代采样：

$$x_i^m=x_i^{m-1}+{ϵ}_i{s}_{{\theta }^{\star }}(x_i^{m-1},{\sigma }_i)+\sqrt{2{ϵ}_i}{z}_i^m,m=1,2,\dots ,M(2)$$

其中：

• ${ϵ}_i>0$ 为步长；
• $z_i^m$服从标准正态分布$(z_i^m\sim \mathcal{N}(0,I)$）。

采样过程按噪声尺度从大到小依次执行$(i=N,N-1,\dots ,1$）：

• 初始采样：$x_N^0\sim \mathcal{N}(x;0,{\sigma }_{\text{max}}^{2}I)$（从最大噪声尺度的高斯分布开始）；
• 尺度衔接：当 (i < N) 时，前一尺度的最终采样结果作为当前尺度的初始值，即$x_i^0=x_{i+1}^M$。

在一定正则性条件下，当所有尺度的迭代步数$M\to \infty$ 且步长 ${ϵ}_i\to 0$ 时，最小噪声尺度对应的最终采样结果$x_1^M$ 成为 $p_{{\sigma }_{\text{min}}}(x)\approx p_{\text{data}}(x)$的精确样本（即原始数据分布的样本）。

去噪扩散概率模型(DDPM)

Sohl-Dickstein 等人（2015）、Ho 等人（2020）提出考虑一组正噪声尺度序列$0<{\beta }_1,{\beta }_2,\dots ,{\beta }_N<1$。对于每个服从数据分布的训练样本$x_0\sim p_{\text{data}}(x)$，构造离散马尔可夫链$\{x_0,x_1,\dots ,x_N\}$，满足：

• 转移概率 $(p(x_i|x_{i-1})=\mathcal{N}(x_i;\sqrt{1-{\beta }_i}{x}_{i-1},{\beta }_{i}I)$（从 $x_{i-1}$ 到 $x_i$的单步扰动规则）；

通俗理解：比如 $x_{i-1}$是 “轻度模糊的照片” (保留 $x_{i-1}$ 的核心特征)，乘以 $\sqrt{1-{\beta }_i}$ 后 “稍微缩小特征幅值” ，再加方差为${\beta }_i$的噪声，得到 “更模糊一点的照片$x_i$” (${\beta }_i$越小，噪声越弱)。

• 由此可推导得累积转移概率$p_{{\alpha }_i}(x_i|x_0)=\mathcal{N}(x_i;\sqrt{{\alpha }_i}{x}_0,(1-{\alpha }_i)I)$（从 $x_0$ 直接到 $x_i$的多步累积扰动），其中${\alpha }_i:={\prod }_{j=1}^i(1-{\beta }_j)$（累积保持系数，随 i 增大而减小）。-----------（由于该过程是马尔科夫链，从初始数据$x_0$到最终噪声$x_T$的完成轨迹的的联合概率分布，可以表示为所有单步转移概率的连乘）

由于每一步扰动都是独立高斯噪声，N 步累积后仍服从高斯分布（高斯分布的可加性）；
$\sqrt{{\alpha }_i}$ 是原始数据 $x_0$经过 i 步扰动后的 “特征保留比例”，$1-{\alpha }_i$ 是 “累积噪声比例”.

与 SMLD 类似，扰动后的数据分布可表示为 $p_{{\alpha }_i}(\tilde{x}):=\int p_{\text{data}}(x)p_{{\alpha }_i}(\tilde{x}|x)dx$（所有原始数据经 i 步扰动后，扰动样本的整体分布）。噪声尺度的设置需满足：最终状态$x_N$近似服从标准高斯分布$\mathcal{N}(0,I)$（完全噪声状态）。

反向过程中，变分马尔可夫链经过以下概率分布参数化：

$$p_{\theta }(x_{i-1}|x_i)=\mathcal{N}\left(x_{i-1};\frac{1}{\sqrt{1-{\beta }_i}}\left(x_i+{\beta }_i{s}_{\theta }(x_i,i)\right),{\beta }_{i}I\right)$$

模型训练采用证据下界（ELBO）的重加权变体，优化目标为：

$${\theta }^{\star }=\arg \underset{\theta }{\min }\sum _{i=1}^N(1-{\alpha }_i){\mathbb{E}}_{p_{\text{data}}(x)}{\mathbb{E}}_{p_{{\alpha }_i}(\tilde{x}|x)}\left[{\Vert s_{\theta }(\tilde{x},i)-{\nabla }_{\tilde{x}}\log p_{{\alpha }_i}(\tilde{x}|x)\Vert }_2^2\right](3)$$

经过公式（3）求得最优模型$s_{{\theta }^{\star }}(x,i)$后，生成样本的过程如下：

1. 从标准高斯分布$x_N\sim \mathcal{N}(0,I)$中采样初始噪声样本；
2. 沿估计的反向马尔可夫链从后向前迭代$(i=N,N-1,\dots ,1$）：
   $$x_{i-1}=\frac{1}{\sqrt{1-{\beta }_i}}\left(x_i+{\beta }_i{s}_{{\theta }^{\star }}(x_i,i)\right)+\sqrt{{\beta }_i}{z}_i(4)$$

其中 $z_i\sim \mathcal{N}(0,I)$为标准正态噪声。

• $s_{{\theta }^{\star }}(x_i,i)={\nabla }_x\log p_{{\alpha }_i}(x_i)$，即 “噪声样本 $x_i$所在分布的梯度方向”—— 这个方向就是 “概率密度增加最快的方向”，也就是 “最可能的去噪方向”.
• 正向过程中，${\beta }_i$是 “第 i 步加的噪声强度”；反向过程中，去噪幅度必须和加噪强度对应—— 加的噪声越多$({\beta }_i$越大），去噪幅度就越大；
• 当前噪声样本$x_i$ 包含 “噪声 + 少量原始特征”，加上 “校准后的去噪调整幅度”，相当于 “减去噪声带来的偏差”。
• 正向过程中，单步转移概率的均值是 $\sqrt{1-{\beta }_i}\cdot x_{i-1}$（即 “清晰样本$x_{i-1}$乘以小于 1 的系数，再叠加噪声得到$x_i$”）；反向过程中，需要除以这个系数，把 “初步去噪后的样本” 还原到原始幅值范围，避免样本数值被过度压缩。

我们将该采样方法称为祖先采样（ancestral sampling）—— 其本质是对概率图模型${\prod }_{i=1}^N{p}_{\theta }(x_{i-1}|x_i)$执行祖先采样。公式（3）对应的目标函数即为 Ho 等人（2020）中的$L_{\text{simple}}$去噪分数匹配目标的加权和，这意味着最优模型就是，此处采用与公式（1）更具相似性的形式书写。与公式（1）类似，公式（3）也$s_{{\theta }^{\star }}(\tilde{x},i)$会匹配扰动数据分布的分数函数${\nabla }_x\log p_{{\alpha }_i}(x)$。

值得注意的是，公式（1）和（3）中第 i 项求和的权重（分别为${\sigma }_i^2$ 和 $(1-{\alpha }_i)$），与对应扰动核的函数形式存在相同关联：${\sigma }_i^2\propto 1/\mathbb{E}\left[{\Vert {\nabla }_x\log p_{{\sigma }_i}(\tilde{x}|x)\Vert }_2^2\right]$，且 $(1-{\alpha }_i)\propto 1/\mathbb{E}\left[{\Vert {\nabla }_x\log p_{{\alpha }_i}(\tilde{x}|x)\Vert }_2^2\right]$（权重与条件分数函数的二阶矩成反比）。

特征	DDPM	NCSN
噪声尺度表示	步数 i + 累积保持系数${\alpha }_i$	直接用噪声尺度${\sigma }_i$
正向过程	离散马尔可夫链（逐步轻微加噪）	单步固定尺度加噪（多尺度并行）
反向采样算法	祖先采样（固定方差高斯分布）	朗之万 MCMC（梯度引导 + 随机探索）
训练目标来源	变分推断 ELBO（等价分数匹配）	直接去噪分数匹配
核心优势	采样速度快（固定步数迭代）	生成样本多样性更好

运用SDE扰动材料

将数据通过无限多个噪声尺度进行连续扰动，使得扰动后的分布随噪声强度增加而遵循 SDE 演化，最终从原始数据分布转化为易于采样的先验分布 “分数扩散模型”（Score-Based Diffusion Models）的核心思想。就是。这

“生成模型要造出自带‘真实感’的扰动数据，关键是得有不同强度的噪声 —— 不是只加一次固定噪声，而是用随机微分方程（SDE）让噪声‘连续加码’。
为啥要这么做呢？原来的数据里，有的地方信息点挤得密（密度高），有的地方稀稀拉拉（密度低）。倘若直接在原始数据里瞎采样，大概率会抽到那些稀疏的‘冷门区域’，很难覆盖到大家想要的目标点。而用SDE 让噪声慢慢增强，就像给数据点‘逐步松绑’：随着噪声强度一点点变大，原本集中在高密度区的数据会慢慢扩散开来，稀疏区也能被均匀覆盖，这样采样时就更容易碰到我们需要的目标点，最后还能让内容从原始分布平滑变成好采样的纯噪声分布，为后续生成真实数据打基础。”

扩散过程的定义：构造一个由连续时间变量$t\in [0,T]$索引的扩散过程$\{x(t){\}}_{t=0}^T$，满足：

• $x(0)\sim p_0$：初始状态服从原始数据分布（$p_0$），即我们有独立同分布（i.i.d.）的样本数据集；
• $x(T)\sim p_T$：最终状态服从先验分布（$p_T$），这是一种易于高效生成样本的 “便捷分布”（如高斯分布）。

直观理解：随着时间 t 从 0 增加到 T，数据$x(t)$逐渐被噪声 “污染”，从真实数据分布$p_0$平滑过渡到先验分布$p_T$（如纯噪声分布）。

• $p_t(x)$：状态 $x(t)$在时间 t 的概率密度函数，描述 t 时刻数据的分布；$p_{s\to t}(x(t)|x(s))$：
• 转移核（transition kernel）—— 描述从时间 s 的状态$x(s)$演化到时间 t 的状态$x(t)$的条件概率分布（$0\le s<t\le T$）。

该扩散过程被建模为伊藤型随机微分方程（Ito SDE）：
$$dx=f(x,t)dt+g(t)dw$$

• w：标准维纳过程（Wiener Process，即布朗运动）—— 核心随机源，引入噪声扰动；
• $f(\cdot ,t):{\mathbb{R}}^d\to {\mathbb{R}}^d$：漂移系数（drift coefficient）—— 向量值函数，描述系统的确定性演化趋势；
• $g(\cdot ):\mathbb{R}\to \mathbb{R}$：扩散系数（diffusion coefficient）—— 标量函数，描述随机扰动的强度，仅与时间 t 相关

只要系数 f 和 g 在状态和时间上满足全局利普希茨条件（Lipschitz condition），SDE 就存在唯一强解（ksendal, 2003）—— 若不满足利普希茨条件：比如$f(x,t)=x^2$（变化率无上限），SDE 可能出现 “解爆炸”（(x(t)) 随时间趋于无穷大）或 “解不唯一”（同一噪声下，数据可能扩散到两个完全不同的方向）。

全局利普希茨条件（Lipschitz condition）:函数的变化率有明确上限，不会 “突变”。
对 SDE 中的系数$f(x,t)$（漂移系数）和$g(x,t)$（扩散系数），全局利普希茨条件要求：存在一个固定常数 (L > 0)（利普希茨常数），对任意两个状态 (x_1、x_2) 和任意时间$t\in [0,T]$，都满足：
$$\Vert f(x_1,t)-f(x_2,t)\Vert \le L\cdot \Vert x_1-x_2\Vert$$$$|g(x_1,t)-g(x_2,t)\Vert \le L\cdot \Vert x_1-x_2\Vert$$不管在什么状态、什么时间，两个状态的 “距离” 乘以 L，总能 “管住” 系数 f（或 g）在这两个状态下的 “差值”。

强解（Strong Solution）SDE 的解是 “随机过程 (x(t))”.
强解的核心是：解 (x(t)) 完全由随机源（布朗运动 (w(t))）决定。通俗理解：给定一个固定的布朗运动轨迹（比如 “某一次噪声的具体建立”），对应的 SDE 解是唯一的 “解和布朗运动一起被确定”，同一噪声轨迹可能对应多个解，无法直接用于数值计算（所以生成模型、工程场景都必须强解）。就是。反之，“弱解” 则

通过反向随机微分方程生成样本

从服从先验分布$x(T)\sim p_T$的样本出发，反向执行上述扩散过程，即可得到服从原始数据分布$x(0)\sim p_0$ 的样本。

Anderson (1982) 的一项关键研究结果表明：扩散过程的反向过程同样是一个扩散过程—— 该过程沿时间反向运行，由反向时间随机微分方程（reverse-time SDE） 描述：
$$dx=\left[f(x,t)-g(t{)}^2{\nabla }_x\log p_t(x)\right]dt+g(t)d\bar{w}（6）$$

其中：

• $\bar{w}$：当时间从 T 反向流向 0 时的标准维纳过程（布朗运动）；
• dt：无穷小的负时间步长（体现 “时间反向”）；
• ${\nabla }_x\log p_t(x)$：各边缘分布$p_t(x)$ 的分数函数（score function），即对数概率密度关于状态 x 的梯度。只要已知所有时间 t 下边缘分布的分数函数${\nabla }_x\log p_t(x)$，就能通过公式（6）推导得到反向扩散过程，并通过模拟该过程从先验分布$p_T$中采样得到原始数据分布$p_0$ 的样本。

核心差异在于漂移项多了 “分数函数修正项”$-g(t{)}^2{\nabla }_x\log p_t(x)$，这是反向过程能 “去噪声、还原数据” 的核心：在正向趋势基础上，用分数函数 “修正方向”，引导样本从噪声向数据的高密度区域移动（即 “去模糊”）。

若 (x(t)) 是模糊照片中的一个像素，分数函数会引导该像素向 “清晰照片中对应像素的位置” 移动。
反向过程没有 “真实数据标签”，全靠分数函数给予 “去噪声的方向指引”，这也是 “基于分数的生成模型” 名称的由来。

基于分数的生成模型（通过SDE实现）“正向扩散-逆向生成”双过程，如下图所示：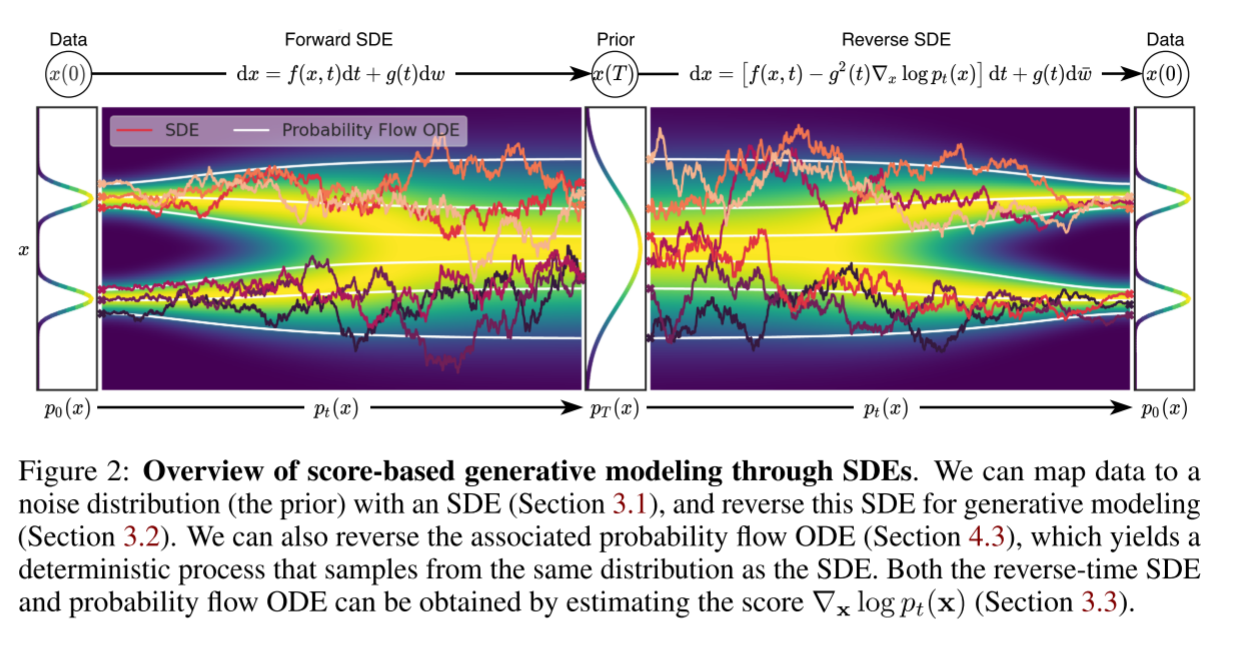

评估SDE的分数

分布的分数函数可通过分数匹配（score matching） 办法，在样本上训练基于分数的模型来估计（Hyvärinen, 2005; Song et al., 2019a）。为估计${\nabla }_x\log p_t(x)$，我们可通过对公式（1）和（3）的连续时间推广，训练一个依赖时间的基于分数的模型$s_{\theta }(x,t)$，其优化目标为：

$${\theta }^{\star }=\arg \underset{\theta }{\min }{\mathbb{E}}_t\left\{\lambda (t){\mathbb{E}}_{p_0(x)}{\mathbb{E}}_{p_{0\to t}(x(t)|x(0))}\left[{\Vert s_{\theta }(x(t),t)-{\nabla }_{x(t)}\log p_{0\to t}(x(t)|x(0))\Vert }_2^2\right]\right\}(7)$$

其中：

• $\lambda :[0,T]\to {\mathbb{R}}_{>0}$：正权重函数；

• t：在 $[0,T]$上均匀采样的时间；

• $x(0)\sim p_0(x)$：原始数据样本（服从数据分布$p_0$）；

• $x(t)\sim p_{0\to t}(x(t)|x(0))$：从 $x(0)$经正向 SDE 演化到 t 时刻的扰动样本（服从正向转移核$p_{0\to t}$）；

• ${\nabla }_{x(t)}\log p_{0\to t}(x(t)|x(0))$：条件分布 $p_{0\to t}(x(t)|x(0))$ 关于 $x(t)$的对数概率密度梯度（即 “条件分数函数”）。

当数据量和模型容量足够时，分数匹配可保证公式（7）的最优解$s_{{\theta }^{\star }}(x,t)$，在几乎所有 x 和 t 下都等于目标分数函数${\nabla }_x\log p_t(x)$。与 SMLD 和 DDPM 类似，权重函数通常可选择$\lambda (t)\propto 1/\mathbb{E}\left[{\Vert {\nabla }_{x(t)}\log p_{0\to t}(x(t)|x(0))\Vert }_2^2\right]$（即与条件分数函数的二阶矩成反比）。

权重函数 $\lambda (t)$：解决 “不同时间分数函数难度差异”问题：不同时间 t 下，条件分数函数${\nabla }_{x(t)}\log p_{0\to t}(x(t)|x(0))$ 的 “波动幅度” 不同（比如 t 接近 0 时，内容扰动小，分数函数波动大；t 接近 T 时，内容接近噪声，分数函数波动小）--------------- 给波动大的 t 分配更大权重，波动小的 t 分配更小权重，避免模型被 “容易学习的时间步” 主导；-------------$\lambda (t)$与条件分数函数的二阶矩成反比（即$\lambda (t)\propto 1/\mathbb{E}[\Vert \cdot {\Vert }_2^2]$），相当于 “难学的时间步多花精力，易学的少花精力”。

公式（7）采用的是去噪分数匹配（denoising score matching）, 为高效求解公式（7），我们通常得已知正向转移核$p_{0\to t}(x(t)|x(0))$

• 当漂移系数 $f(\cdot ,t)$为仿射函数（affine function，如线性函数加常数项）时，转移核$p_{0\to t}$高斯分布，其均值和方差通常具有闭合解（解析表达式），可通过标准办法求得；就是始终
• 对于更一般的 SDE，可借助求解柯尔莫哥洛夫前向方程（Kolmogorov’s forward equation, Øksendal, 2003） 得到$p_{0\to t}$；此外，也可直接模拟正向 SDE 从$p_{0\to t}$中采样，并用切片分数匹配替代公式（7）中的去噪分数匹配进行模型训练 —— 此种方式可绕过条件分数函数${\nabla }_{x(t)}\log p_{0\to t}(x(t)|x(0))$的计算（见附录 A）。

为什么用条件分数函数？：
因为 $p_{0\to t}(x(t)|x(0))$ 的解析形式更容易获取（比如漂移系数为仿射函数时是高斯分布），而$p_t(x)$难以直接计算 —— 用条件分数函数作为训练目标，是一种 “迂回逼近” 真实分数函数的策略；

获取方式	适用场景	核心特点
闭合解（解析形式）	漂移系数 $f(\cdot ,t)$为仿射函数（如线性函数）	最快最精准，直接写出均值和方差（如高斯分布）
求解柯尔莫哥洛夫前向方程	一般形式的 SDE（无解析解）	偏微分方程求解，数学严谨但计算复杂
直接模拟 SDE 采样	所有 SDE（尤其是无解析解的情况）	工程上最常用，通过数值方法（如欧拉 - 马尔可夫）生成扰动样本，无需计算分布解析形式

示例: VE, VP SDES AND BEYOND

SMLD 和 DDPM 中使用的噪声扰动可视为两种不同随机微分方程（SDE）的离散化形式。以下进行简要讨论，更多细节请参见附录 B。

当使用共 N 个噪声尺度时，SMLD 的每个扰动核$p_{{\sigma }_i}(x|x_0)$对应如下马尔可夫链中$x_i$ 的分布：

$$x_i=x_{i-1}+\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}{z}_{i-1},i=1,\dots ,N(8)$$

SMLD 的通过递增的噪声尺度逐步扰动内容就是核心，最终让数据分布变为纯噪声。公式（8）的推导基于高斯噪声的方差可加性：
为了从 $x_{i-1}$（方差 ${\sigma }_{i-1}^2$）过渡到 $x_i$（方差 ${\sigma }_i^2$），要求添加 “方差增量” 为 ${\sigma }_i^2-{\sigma }_{i-1}^2$的高斯噪声。根据高斯分布的可加性：若$x_{i-1}\sim \mathcal{N}(x_0,{\sigma }_{i-1}^{2}I$)，且添加独立噪声$\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}{z}_{i-1}$（其中 $z_{i-1}\sim \mathcal{N}(0,I)$），则：$x_i=x_{i-1}+\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}{z}_{i-1}$此时 $x_i$ 的方差为：$$\text{Var}(x_i)=\text{Var}(x_{i-1})+\text{Var}\left(\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}{z}_{i-1}\right)={\sigma }_{i-1}^2+({\sigma }_i^2-{\sigma }_{i-1}^2)={\sigma }_i^2$$即 $x_i\sim \mathcal{N}(x_0,{\sigma }_i^{2}I)$，满足设计目标。

其中 $z_{i-1}\sim \mathcal{N}(0,I)$，且为简化符号引入${\sigma }_0=0$。当 $N\to \infty$ 时，$\{{\sigma }_i{\}}_{i=1}^N$ 变为函数 $\sigma (t)$，$z_i$ 变为 $z(t)$，马尔可夫链 $\{x_i{\}}_{i=1}^N$变为连续随机过程$\{x(t){\}}_{t=0}^1$（此处用连续时间变量$t\in [0,1]$索引，而非整数 i）。该过程由以下 SDE 描述：
$$dx=\sqrt{\frac{d[{\sigma }^2(t)]}{dt}}dw(9)$$

$\Delta x_i=x_i-x_{i-1}=\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}\cdot z_{i-1}$
当 $N\to \infty$时，时间步长$\Delta t=\frac{1}{N}\to 0$，此时：

• ${\sigma }_i^2-{\sigma }_{i-1}^2\approx \frac{d[{\sigma }^2(t)]}{dt}\cdot \Delta t$（函数的微分近似，即$df(t)\approx f^{\prime }(t)\Delta t$）；
• $z_{i-1}\cdot \sqrt{\Delta t}\approx dw(t)$（布朗运动的增量性质：$w(t+\Delta t)-w(t)\sim \mathcal{N}(0,\Delta tI$)，因此 $z_{i-1}\sqrt{\Delta t}$ 是 $dw(t)$的离散近似）。
  将上述近似代入增量式$\Delta x_i$，得到：$$\Delta x\approx \sqrt{\frac{d[{\sigma }^2(t)]}{dt}\cdot \Delta t}\cdot \frac{dw(t)}{\sqrt{\Delta t}}=\sqrt{\frac{d[{\sigma }^2(t)]}{dt}}\cdot dw(t)$$当 $\Delta t\to 0$时，增量形式过渡为微分形式，即：$dx=\sqrt{\frac{d[{\sigma }^2(t)]}{dt}}dw$

类似地，对于 DDPM 的扰动核$\{p_{{\alpha }_i}(x|x_0){\}}_{i=1}^N$，其离散马尔可夫链为：
$$x_i=\sqrt{1-{\beta }_i}{x}_{i-1}+\sqrt{{\beta }_i}{z}_{i-1},i=1,\dots ,N(10)$$

DDPM 的核心是通过 “保留特征 + 添加噪声” 的方式逐步扰动数据，最终让数据分布变为纯高斯噪声。
第 i 步的扰动后分布$p_{{\alpha }_i}(x_i|x_0)$ 是方差为 $1-{\alpha }_i$的高斯分布（其中${\alpha }_i={\prod }_{j=1}^i(1-{\beta }_j)$，初始 ${\alpha }_0=1$）。
为了从 $x_{i-1}$（满足 $x_{i-1}\sim \mathcal{N}(\sqrt{{\alpha }_{i-1}}{x}_0,(1-{\alpha }_{i-1})I)$）过渡到 $x_i$，需对 $x_{i-1}$ 做 “缩放 + 加噪声” 操作：$x_i=\sqrt{1-{\beta }_i}{x}_{i-1}+\sqrt{{\beta }_i}{z}_{i-1}$其中 $z_{i-1}\sim \mathcal{N}(0,I)$。
验证 $x_i$ 的分布：
均值：$$\mathbb{E}[x_i]=\sqrt{1-{\beta }_i}\cdot \sqrt{{\alpha }_{i-1}}{x}_0=\sqrt{(1-{\beta }_i){\alpha }_{i-1}}{x}_0=\sqrt{{\alpha }_i}{x}_0$$（因为 ${\alpha }_i=(1-{\beta }_i){\alpha }_{i-1}$）；
方差：$$\text{Var}(x_i)=(1-{\beta }_i)\cdot (1-{\alpha }_{i-1})+{\beta }_i\cdot 1=1-{\beta }_i-(1-{\beta }_i){\alpha }_{i-1}+{\beta }_i=1-(1-{\beta }_i){\alpha }_{i-1}=1-{\alpha }_i$$
因此，$x_i\sim \mathcal{N}(\sqrt{{\alpha }_i}{x}_0,(1-{\alpha }_i)I)$，满足设计目标。

当 $N\to \infty$时，公式（10）收敛到如下 SDE：

$$dx=-\frac{1}{2}\beta (t)xdt+\sqrt{\beta (t)}dw(11)$$

$\Delta x_i=x_i-x_{i-1}=\left(\sqrt{1-{\beta }_i}-1\right)x_{i-1}+\sqrt{{\beta }_i}{z}_{i-1}$
当 ${\beta }_i\ll 1$（因 $N\to \infty$，${\beta }_i=\beta (t)\Delta t\ll 1$），利用泰勒展开$\sqrt{1-ϵ}\approx 1-\frac{ϵ}{2}-\frac{{ϵ}^2}{8}-\dots$，取一阶近似：$\sqrt{1-{\beta }_i}-1\approx -\frac{{\beta }_i}{2}=-\frac{\beta (t)\Delta t}{2}$
布朗运动的增量满足$w(t+\Delta t)-w(t)\sim \mathcal{N}(0,\Delta tI)$，因此 $z_{i-1}\sqrt{\Delta t}\approx dw(t)$（即 $z_{i-1}\approx \frac{dw(t)}{\sqrt{\Delta t}}$）。代入得：$$\sqrt{{\beta }_i}{z}_{i-1}=\sqrt{\beta (t)\Delta t}\cdot \frac{dw(t)}{\sqrt{\Delta t}}=\sqrt{\beta (t)}dw(t)$$
将上述近似代入$\Delta x_i$：
$$\Delta x_i\approx -\frac{\beta (t)\Delta t}{2}{x}_{i-1}+\sqrt{\beta (t)}dw(t)$$
当 $\Delta t\to 0$ 时，$x_{i-1}\approx x(t)$（连续过程的近似），增量$\Delta x_i$过渡为微分 dx，因此：$$dx=-\frac{1}{2}\beta (t)xdt+\sqrt{\beta (t)}dw(t)$$

因此，SMLD 和 DDPM 中启用的噪声扰动分别对应公式（9）和（11）这两种 SDE 的离散化形式。

结尾

好文推荐：

生成扩散模型漫谈：一般框架之SDE篇

扩散模型（Diffusion Models）详解