代码改变世界

深入解析：神经网络反向传播：原理、算法与实现

2026-01-02 20:30  tlnshuju  阅读(4)  评论(0)    收藏  举报

一、反向传播算法概述
反向传播（Backpropagation）是神经网络训练中最核心的算法之一，它利用链式法则高效地计算损失函数相对于网络参数的梯度。该算法由Rumelhart、Hinton和Williams于1986年系统性地提出，已成为现代深度学习的基础。

核心思想
反向传播通过"前向传播"计算网络输出和损失，然后借助"反向传播"将误差从输出层逐层传回输入层，计算各层参数的梯度，末了利用梯度下降法更新参数。

二、数学原理

  1. 链式法则
    对于复合函数f(g(x))f(g(x))f(g(x))，其导数为：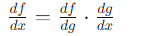
    在这里插入图片描述
    在神经网络中，损失函数LLL 关于参数 www 的梯度为：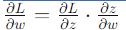
    在这里插入图片描述
    其中 zzz 是 www所在层的输出。
  2. 激活函数的导数
    常用激活函数及其导数：

Sigmoid:σ(x)=11+e−x\sigma(x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1​, σ′(x)=σ(x)(1−σ(x))\sigma'(x) = \sigma(x)(1-\sigma(x))σ′(x)=σ(x)(1−σ(x))

ReLU: f(x)=max⁡(0,x)f(x) = \max(0, x)f(x)=max(0,x), f′(x)={ 1if x>0 0otherwisef'(x) = \begin{cases} 1 & \text{if } x > 0 \ 0 & \text{otherwise} \end{cases}f′(x)={ 1​if x>00​otherwise​

Tanh: tanh⁡(x)=ex−e−xex+e−x\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}tanh(x)=ex+e−xex−e−x​, tanh⁡′(x)=1−tanh⁡2(x)\tanh'(x) = 1 - \tanh^2(x)tanh′(x)=1−tanh2(x)

三、反向传播算法步骤
算法流程

1. 初始化网络参数（权重和偏置）
2. 重复以下步骤直到收敛：
a. 前向传播：计算每一层的激活值
b. 计算输出层误差：δ