完整教程：Transformer的Lora微调机制详解

Lora理论介绍

Lora（LOW-RANK ADAPTATION）的核心思想就是在微调Transformer时，只对Transformer的attention部分的QKVO的变换矩阵W进行低秩微调。

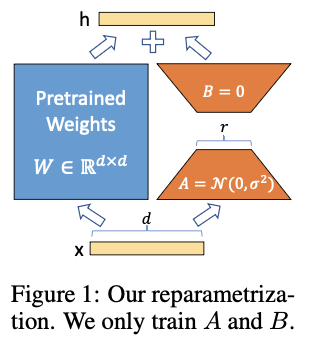
其中A矩阵为随机初始化的，B为全0矩阵

为什么A是随机初始化，B为0初始化，而不是反过来？

相关解答：

https://zhuanlan.zhihu.com/p/17191065380https://zhuanlan.zhihu.com/p/17191065380相关论文：The Impact of Initialization on LoRA Finetuning Dynamics专门讨论了这个问题。论文的结果说明：

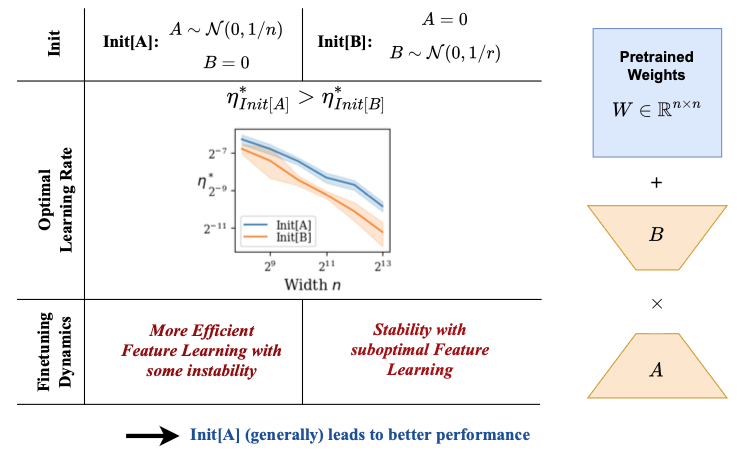
1，其实两种初始化的方式都可以训起来

2，初始化A矩阵的方式，最后得到的loss会更小

3，初始化A矩阵的方式，学习率可以调的更大，模型更容易训练

总之就是初始化A的方式比较好。但是反过来也是可以的

lora参数设置

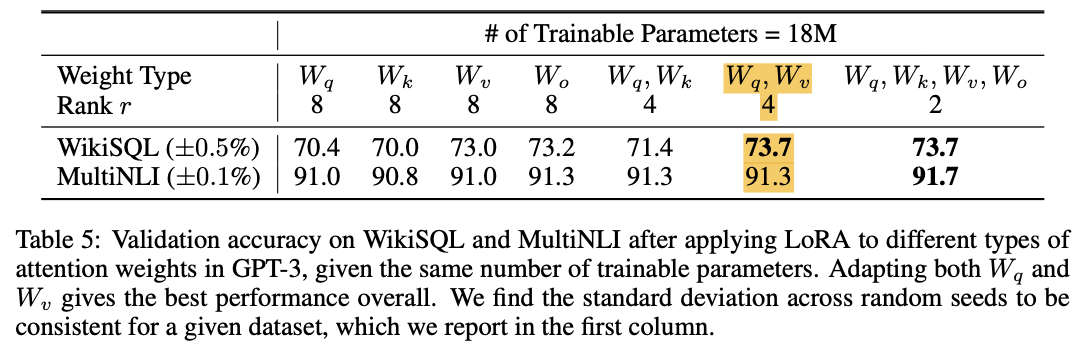
 原文中很多实验都只对Q和V的权重矩阵施加了lora

一般情况下，只需要对Transformer中的Q V矩阵做lora，并将rank设置为4就可以取得很好的效果

lora在上Delta W还有一个超参alpha

对做一个scaling， 其方式是alpha / rank

这样在确定了alpha之后，在调rank时就不用再管学习率的问题

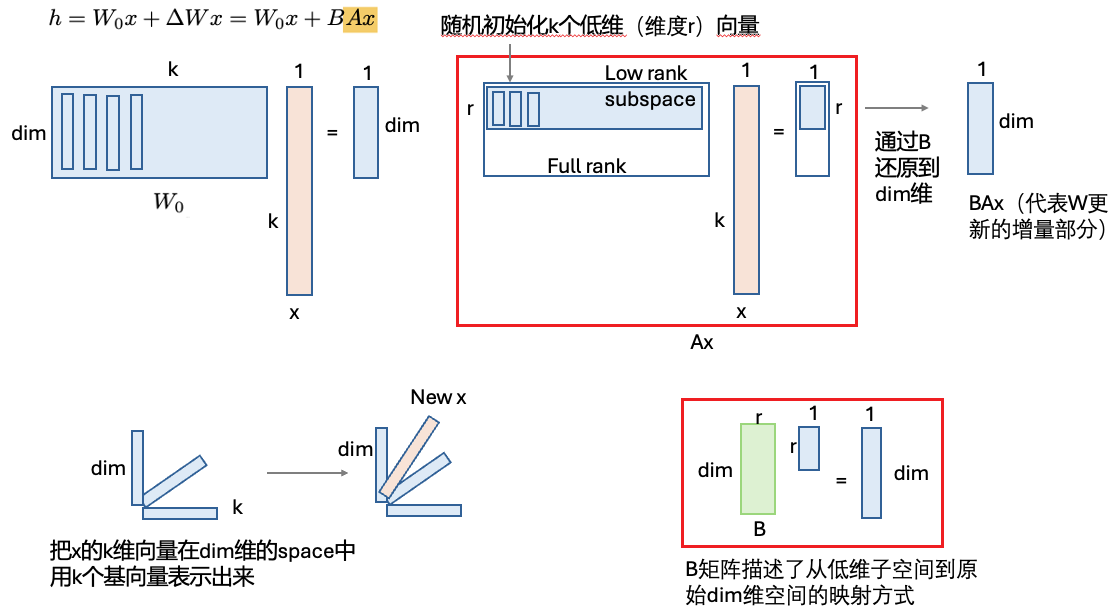
Lora具体的计算方式：

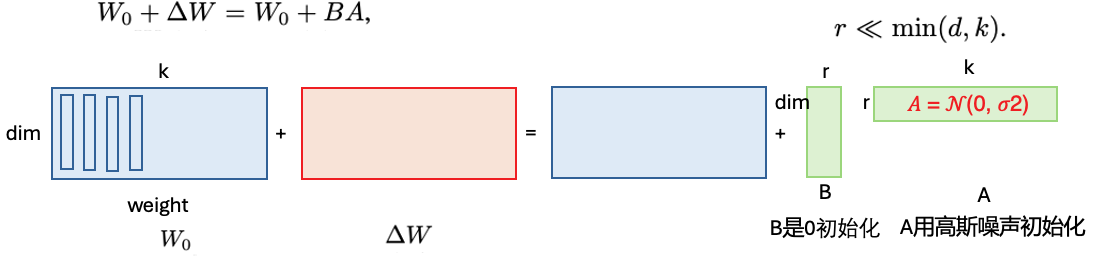
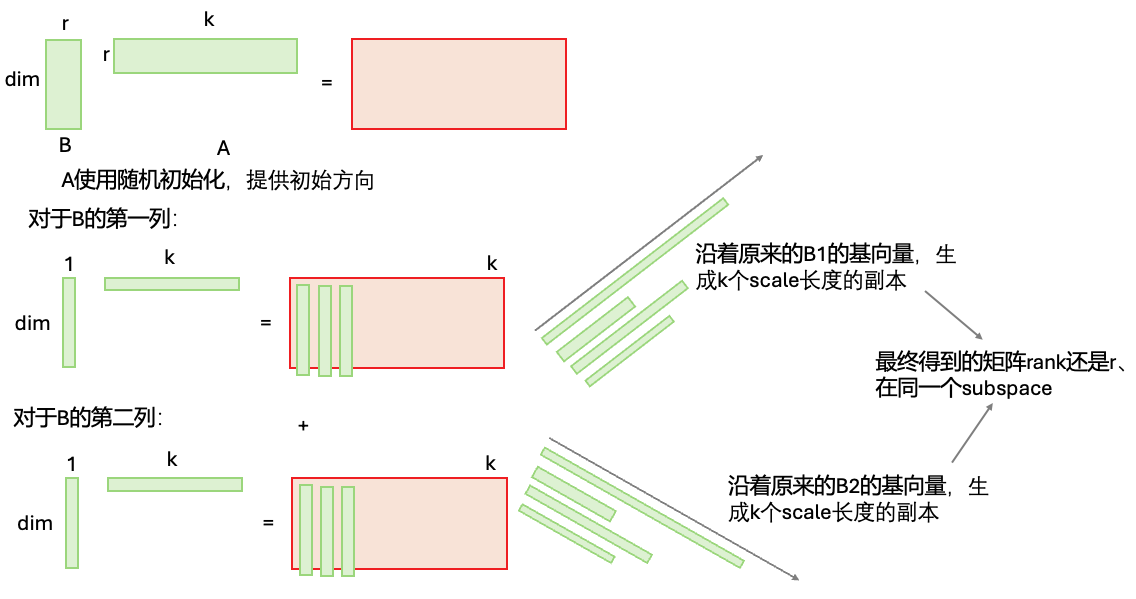
补充知识：为什么两个向量相乘，得到的矩阵的秩还是1:

---

Lora的Pytorch代码实现：

代码实现其实非常简单

大致使用方法：

import torch.nn as nn
# 使用nn.Parameter 来初始化A B矩阵
# LoRALinear
self.A = nn.Parameter(torch.randn(r, self.in_features) * 0.01)
self.B = nn.Parameter(torch.zeros(self.out_features, r))
#缩放因子
self.scale = alpha / r if r > 0 else 1.0
# 使用LoRALinear附加到原来的线性层变换矩阵上
out = self.orig_linear(x) # 原始的矩阵output
# 使用lora来更新output
# x_d @ A.T shape: (..., r)
lora_intermediate = torch.matmul(x_d, self.A.t()) # [batch, seq_len, d_model] @ [d_model, r] -> [batch, seq_len, r]
# (..., r) @ B.t -> (..., out)
lora_out = torch.matmul(lora_intermediate, self.B.t()) * self.scale # 还要乘一个scale # [batch, seq_len, r] @ [r, out] -> [batch, seq_len, out]
out = out + lora_out # out = [batch, seq_len, d_model]
# 在使用时，用LoRALinear 来替换目标位置原来的linear层
orig_linear = getattr(parent, attr)
lora_linear = LoRALinear(orig_linear, r=r, alpha=alpha, dropout=dropout) # 替换原来的linear层
setattr(parent, attr, lora_linear)
replaced.append(name)

完整代码：

import torch
import torch.nn as nn
class LoRALinear(nn.Module):
    """
    LoRA wrapper for an nn.Linear layer.
    It keeps the original weight (frozen) and adds a low-rank update BA (trainable).
    W' = W + scale * B @ A   where A shape = (r, in_features), B shape = (out_features, r)
    """
    def __init__(self, orig_linear: nn.Linear, r: int = 4, alpha: float = 1.0, dropout: float = 0.0):
        super().__init__()
        # store original linear layer params (frozen)
        self.in_features = orig_linear.in_features
        self.out_features = orig_linear.out_features
        self.orig_linear = orig_linear
        # freeze original weight and bias
        self.orig_linear.weight.requires_grad = False
        if self.orig_linear.bias is not None:
            self.orig_linear.bias.requires_grad = False
        # LoRA params
        self.r = r
        self.alpha = alpha
        self.scale = alpha / r if r > 0 else 1.0
        self.dropout = nn.Dropout(dropout) if dropout > 0.0 else None
        if r > 0:
            # A: down projection (r x in)
            # 在这里设置lora的AB矩阵
            self.A = nn.Parameter(torch.randn(r, self.in_features) * 0.01) # 高斯噪声初始化
            # B: up projection (out x r) initialized to zeros
            self.B = nn.Parameter(torch.zeros(self.out_features, r))
        else:
            # r == 0 means no LoRA
            self.register_parameter('A', None) # 避免state_dict 缺少键名
            self.register_parameter('B', None)
        # Flag whether to merge LoRA into orig weight for fast inference
        self.merged = False
    def forward(self, x):
        '''
        输入 x 形状是 [batch, seq_len, d_model]
        '''
        # original linear output
        out = self.orig_linear(x) # 原始的矩阵output
        if self.r > 0 and not self.merged:
            # compute LoRA update: (x @ A.T) -> shape (..., r), then @ B.T -> (..., out)
            if self.dropout is not None:
                x_d = self.dropout(x)
            else:
                x_d = x
            # x_d @ A.T shape: (..., r)
            lora_intermediate = torch.matmul(x_d, self.A.t()) # [batch, seq_len, d_model] @ [d_model, r] -> [batch, seq_len, r]
            # (..., r) @ B.t -> (..., out)
            lora_out = torch.matmul(lora_intermediate, self.B.t()) * self.scale # 还要乘一个scale # [batch, seq_len, r] @ [r, out] -> [batch, seq_len, out]
            out = out + lora_out # out = [batch, seq_len, d_model]
        return out
    def merge_to_orig(self):
        """Merge LoRA weights into original weight matrix (in-place). After merging,
           you can set merged=True to avoid computing LoRA in forward and optionally
           delete A,B to save memory.
        """
        if self.r <= 0 or self.merged:
            return
        # W' = W + scale * B @ A
        delta = (self.B @ self.A) * self.scale  # shape (out, in)
        # orig_linear.weight is (out, in)
        self.orig_linear.weight.data += delta.data
        self.merged = True
    def unmerge_from_orig(self):
        """Reverse merge if needed. Only works if delta still available or stored externally.
           This is a simple helper; in practice you might avoid unmerge or reload original weights.
        """
        if self.r <= 0 or not self.merged:
            return
        delta = (self.B @ self.A) * self.scale
        self.orig_linear.weight.data -= delta.data
        self.merged = False
# 注入lora
def inject_lora(model: nn.Module, r=4, alpha=1.0, dropout=0.0, filter_fn=None):
    """
    Replace nn.Linear modules in `model` with LoRALinear wrappers.
    filter_fn(name, module) -> bool  if True, replace this linear.
    If filter_fn is None, replace all nn.Linear.
    Returns list of names replaced.
    """
    replaced = []
    for name, module in list(model.named_modules()):
        # We need the parent container to replace attribute; named_modules returns nested names.
        # Skip root
        if isinstance(module, nn.Linear):
            # decide whether to replace (default replace all)
            do_replace = True if filter_fn is None else filter_fn(name, module)
            if not do_replace:
                continue
            # find parent and attribute name
            parent = model
            name_parts = name.split('.')
            for p in name_parts[:-1]:
                parent = getattr(parent, p)
            attr = name_parts[-1]
            orig_linear = getattr(parent, attr)
            lora_linear = LoRALinear(orig_linear, r=r, alpha=alpha, dropout=dropout)
            setattr(parent, attr, lora_linear)
            replaced.append(name)
    return replaced
def qkv_filter(name, module):
    # 根据模型中线性层命名习惯定制
    # 例如 "attn.q_proj", "attn.k_proj", "attn.v_proj" 常见
    low = name.lower()
    return ('q_proj' in low) or ('k_proj' in low) or ('v_proj' in low) or ('q' in low and 'proj' in low)
def get_lora_parameters(model: nn.Module):
    params = []
    for n, p in model.named_parameters():
        if p.requires_grad:
            # if using LoRALinear above, A and B are trainable, orig weights are frozen
            params.append(p)
    return params
# 或者更明确地只收集 A,B
def get_lora_AB(model: nn.Module):
    ab = []
    for m in model.modules():
        if isinstance(m, LoRALinear) and m.r > 0:
            ab.append(m.A)
            ab.append(m.B)
    return ab
# 假设 model 是某个 transformer 模型
# 只给名字包含 'q_proj' 'k_proj' 'v_proj' 的线性层注入
replaced = inject_lora(model, r=8, alpha=32, dropout=0.0, filter_fn=qkv_filter)
print("replaced layers:", replaced)
optimizer = torch.optim.Adam(get_lora_AB(model), lr=1e-4)
# 训练完毕后，为最高效推理可以把 LoRA 合并进原模型权重：
for m in model.modules():
    if isinstance(m, LoRALinear):
        m.merge_to_orig()
# 假设 model 是某个 transformer 模型
# 只给名字包含 'q_proj' 'k_proj' 'v_proj' 的线性层注入
replaced = inject_lora(model, r=8, alpha=32, dropout=0.0, filter_fn=qkv_filter)
print("replaced layers:", replaced)
# 优化器只包含 LoRA 参数
optimizer = torch.optim.Adam(get_lora_AB(model), lr=1e-4)