【动手学深度学习PyTorch】softmax回归 - 实践

softmax回归

一、分类困难

1. 介绍

假设每次输入是一个$2\times 2$的灰度图像。每个图像属于类别“猫”“鸡”和“狗”中的一个。接下来，我们要选择如何表示标签。
选择就是最直接的想法$y\in \{1,2,3\}$，其中整数分别代表$\{\text{狗},\text{猫},\text{鸡}\}$。这是在计算机上存储此类信息的有效方法。

2. 独热编码（one-hot encoding）

独热编码是一个向量，它的分量和类别一样多。

类别对应的分量设置为1，其他所有分量设置为0。
在上边的例子中，标签$y$将是一个三维向量，其中$(1,0,0)$对应于“猫”、$(0,1,0)$对应于“鸡”、$(0,0,1)$​对应于“狗”：$$y\in \{(1,0,0),(0,1,0),(0,0,1)\}.$$

二、网络架构

为了估计所有可能类别的条件概率，我们得一个有多个输出的模型，每个类别对应一个输出。
为了解除线性模型的分类问题，我们必须和输出一样多的仿射函数（affine function）。每个输出对应于它自己的仿射函数。
在我们的例子中，由于我们有4个特征和3个可能的输出类别，我们将需要12个标量来表示权重（带下标的$w$），3个标量来表示偏置（带下标的$b$）。
下面我们为每个输入计算三个未规范化的预测（logit）：$o_1$、$o_2$和$o_3$。
$$\begin{array}{rl}{o}_1& =x_1{w}_{11}+x_2{w}_{12}+x_3{w}_{13}+x_4{w}_{14}+b_1,\\ o_2& =x_1{w}_{21}+x_2{w}_{22}+x_3{w}_{23}+x_4{w}_{24}+b_2,\\ o_3& =x_1{w}_{31}+x_2{w}_{32}+x_3{w}_{33}+x_4{w}_{34}+b_3.\end{array}$$

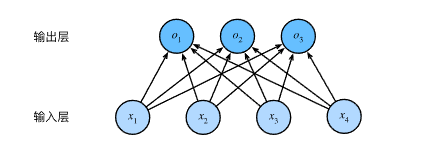
我们许可用神经网络图来描述这个计算过程。
与线性回归一样，softmax回归也是一个单层神经网络。由于计算每个输出$o_1$、$o_2$和$o_3$取决于所有输入$x_1$、$x_2$、$x_3$和$x_4$，因而softmax回归的输出层也是全连接层。

通过向量形式表达为$\mathbf{o}=\mathbf{Wx}+\mathbf{b}$，

三、全连接层的参数开销

全连接层是“完全”连接的，可能有很多可学习的参数。
具体来说，对于任何具有$d$个输入和$q$个输出的全连接层，参数开销为$\mathcal{O}(dq)$，这个数字在实践中可能高得令人望而却步。然而将$d$个输入转换为$q$个输出的成本可以减少到$\mathcal{O}(\frac{dq}{n})$，其中超参数$n$行由我们灵活指定，以在实际应用中平衡参数节约和模型有效性

四、softmax运算

softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。

• 为了做完这一目标，我们首先对每个未规范化的预测求幂，这样可以确保输出非负。
• 为了确保最终输出的概率值总和为1，我们再让每个求幂后的结果除以它们的总和。
• 如下式：$$\hat{\mathbf{y}}=\mathrm{softmax}(\mathbf{o})\text{其中}{\hat{y}}_j=\frac{\exp (o_j)}{{\sum }_k\exp (o_k)}$$
  • 对于所有的$j$总有$0\le {\hat{y}}_j\le 1$。因此，$\hat{\mathbf{y}}$可以视为一个正确的概率分布。

softmax运算不会改变未规范化的预测$\mathbf{o}$之间的大小次序，只会确定分配给每个类别的概率。因此，在预测过程中，我们仍然可以用下式来选择最有可能的类别。
$$\underset{j}{\mathrm{argmax}}{\hat{y}}_j=\underset{j}{\mathrm{argmax}}{o}_j.$$

尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。因此，softmax回归是一个线性模型（linear model）。

五、小批量样本的矢量化

为了提高计算效率并且充分利用GPU，我们通常会对小批量样本的材料执行矢量计算。
假设大家读取了一个批量的样本$\mathbf{X}$，其中特征维度（输入数量）为$d$，批量大小为$n$。此外，假设我们在输出中有$q$个类别。那么小批量样本的特征为$\mathbf{X}\in {\mathbb{R}}^{n\times d}$，权重为$\mathbf{W}\in {\mathbb{R}}^{d\times q}$，偏置为$\mathbf{b}\in {\mathbb{R}}^{1\times q}$。
softmax回归的矢量计算表达式为：

$$\begin{array}{rl}\mathbf{O}& =\mathbf{XW}+\mathbf{b},\\ \hat{\mathbf{Y}}& =\mathrm{softmax}(\mathbf{O}).\end{array}$$

相对于一次处理一个样本，小批量样本的矢量化加快了$\mathbf{X}和\mathbf{W}$的矩阵-向量乘法。
由于$\mathbf{X}$中的每一行代表一个数据样本，那么softmax运算许可按行（rowwise）执行：
对于$\mathbf{O}$的每一行，我们先对所有项进行幂运算，然后凭借求和对它们进行标准化。
在$\begin{array}{rl}\mathbf{O}& =\mathbf{XW}+\mathbf{b}\end{array}$中，$\mathbf{XW}+\mathbf{b}$的求和会使用广播机制，小批量的未规范化预测$\mathbf{O}$和输出概率$\hat{\mathbf{Y}}$都是形状为$n\times q$的矩阵。

六、损失函数

1. 对数似然

softmax函数给出了一个向量$\hat{\mathbf{y}}$，我们能够将其视为“对给定任意输入$\mathbf{x}$的每个类的条件概率”。例如，${\hat{y}}_1$=$P(y=\text{猫}\mid \mathbf{x})$。
假设整个数据集$\{\mathbf{X},\mathbf{Y}\}$具有$n$个样本，其中索引$i$的样本由特征向量${\mathbf{x}}^{(i)}$和独热标签向量${\mathbf{y}}^{(i)}$组成。我们许可将估计值与实际值进行比较：
$$P(\mathbf{Y}\mid \mathbf{X})=\prod _{i=1}^{n}P({\mathbf{y}}^{(i)}\mid {\mathbf{x}}^{(i)}).$$

根据最大似然估计，我们最大化$P(\mathbf{Y}\mid \mathbf{X})$，相当于最小化负对数似然：

$$-\log P(\mathbf{Y}\mid \mathbf{X})=\sum _{i=1}^n-\log P({\mathbf{y}}^{(i)}\mid {\mathbf{x}}^{(i)})=\sum _{i=1}^{n}l({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}),$$

其中，对于任何标签$\mathbf{y}$和模型预测$\hat{\mathbf{y}}$，损失函数为：$ l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j. $

2. softmax及其导数

subsec_softmax_and_derivatives

由于softmax和相关的损失函数很常见，
因此我们需要更好地理解它的计算方式。
将$\hat{\mathbf{y}}=\mathrm{softmax}(\mathbf{o})\text{其中}{\hat{y}}_j=\frac{\exp (o_j)}{{\sum }_k\exp (o_k)}$代入损失$ l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j. $中。
利用softmax的定义，我们得到：
$$\begin{array}{rl}l(\mathbf{y},\hat{\mathbf{y}})& =-\sum _{j=1}^q{y}_j\log \frac{\exp (o_j)}{{\sum }_{k=1}^q\exp (o_k)}\\ & =\sum _{j=1}^q{y}_j\log \sum _{k=1}^q\exp (o_k)-\sum _{j=1}^q{y}_j{o}_j\\ & =\log \sum _{k=1}^q\exp (o_k)-\sum _{j=1}^q{y}_j{o}_j.\end{array}$$

考虑相对于任何未规范化的预测$o_j$的导数，大家得到：

$${\partial }_{o_j}l(\mathbf{y},\hat{\mathbf{y}})=\frac{\exp (o_j)}{{\sum }_{k=1}^q\exp (o_k)}-y_j=\mathrm{softmax}(\mathbf{o}{)}_j-y_j.$$

3. 交叉熵损失

我们启用$ l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j$来定义损失$l$，它是所有标签分布的预期损失值。
此损失称为交叉熵损失（cross-entropy loss），它是分类障碍最常用的损失之一。

小结

• softmax运算获取一个向量并将其映射为概率。
• softmax回归适用于分类障碍，它应用了softmax运算中输出类别的概率分布。
• 一个衡量两个概率分布之间差异的很好的度量，它测量给定模型编码数据所需的比特数。就是交叉熵

---

内容声明
本文基于开源教材《动手学深度学习》（Dive into Deep Learning, 作者：Aston Zhang、Zachary C. Lipton、Mu Li、Alexander J. Smola 等）整理，原始项目地址：https://github.com/d2l-ai/d2l-zh。
在整理过程中对部分内容进行了删改和补充，仅用于个人学习与交流，版权归原作者所有。

---