实用指南：动态规划之买卖股票的最佳时机III和IV

目录

简单介绍

题目连接

思路与代码

动态规划之买卖股票的最佳时机III代码实现

简单分析一下动态规划之买卖股票的最佳时机IV​编辑

动态规划之买卖股票的最佳时机IV的代码实现

---

简单介绍

这两道题是动态规划专题的。这两道题的唯一差距就是交易次数的不同。动态规划之买卖股票的最佳时机III的代码完全可以推广到动态规划之买卖股票的最佳时机IV。

题目连接

123. 买卖股票的最佳时机 III - 力扣（LeetCode）

188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

思路与代码

重点分析动态规划之买卖股票的最佳时机III哦~~~

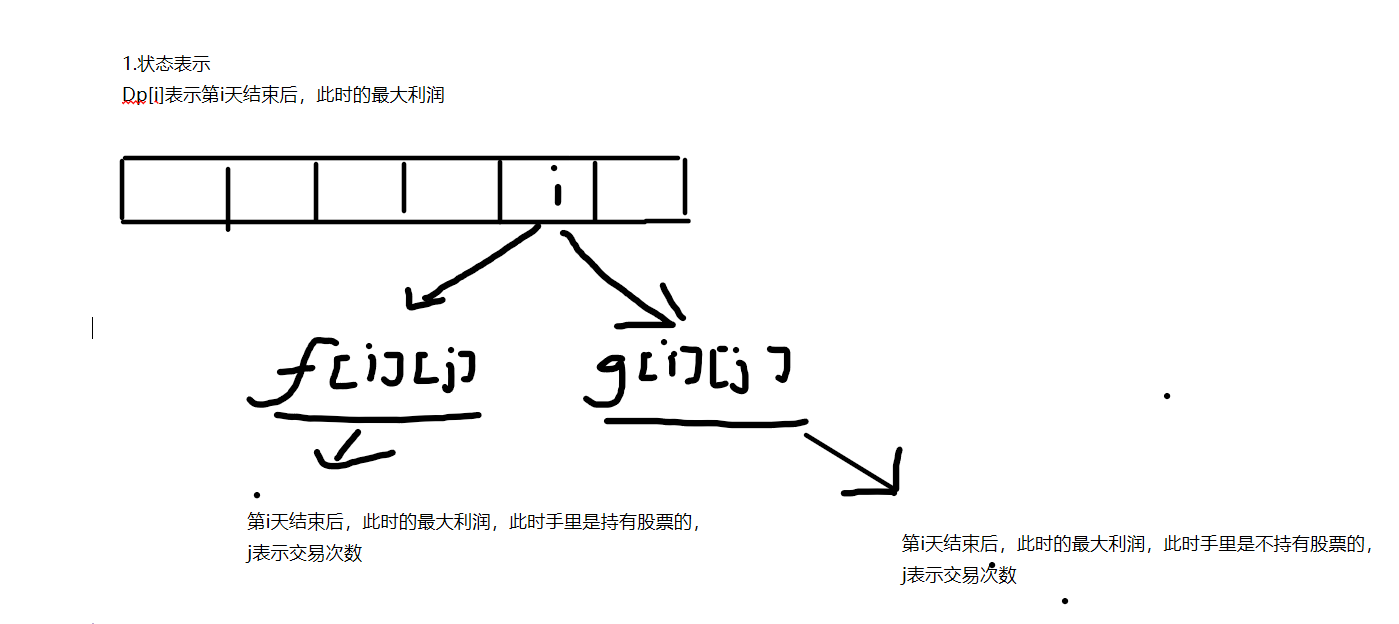
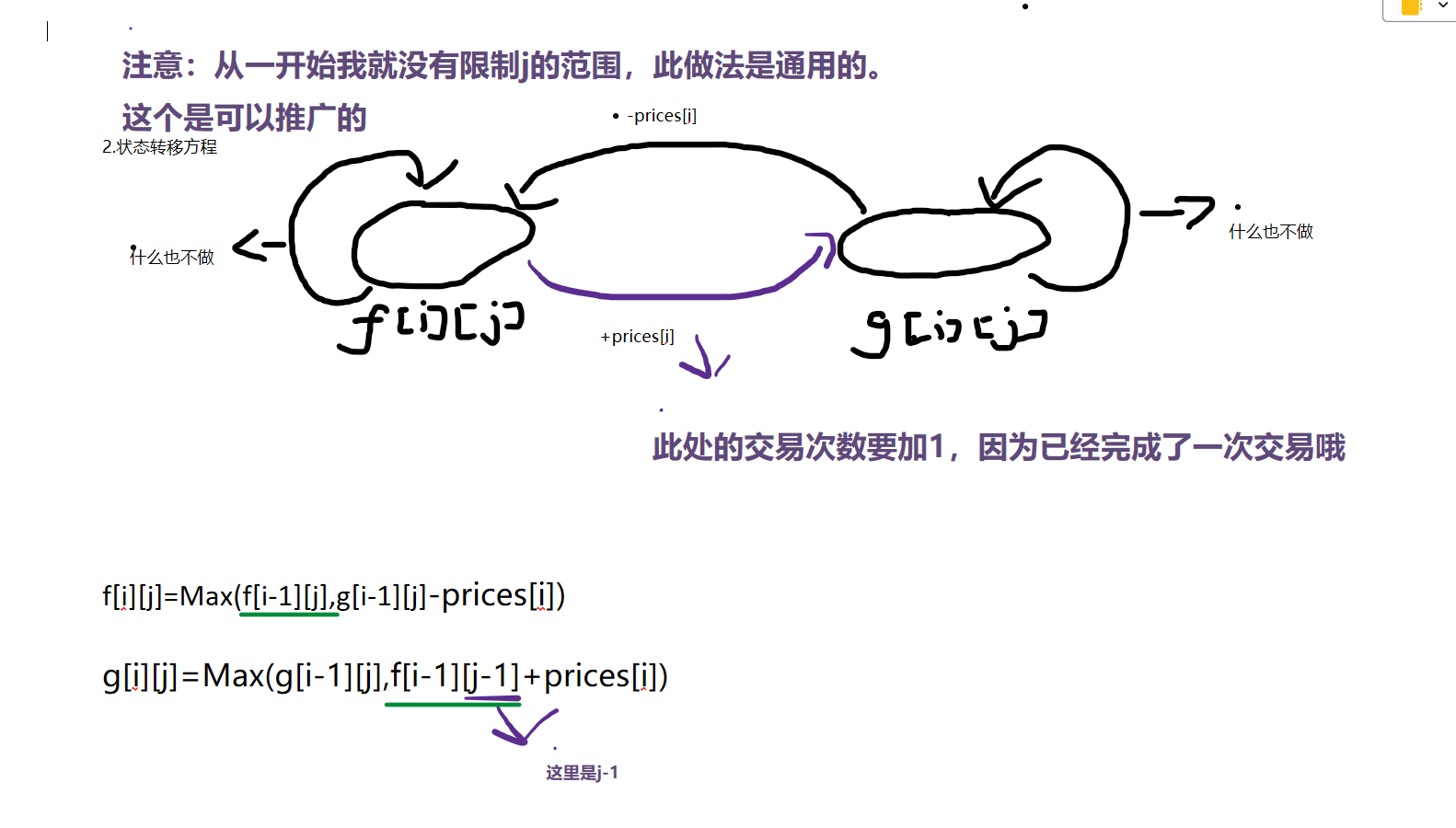
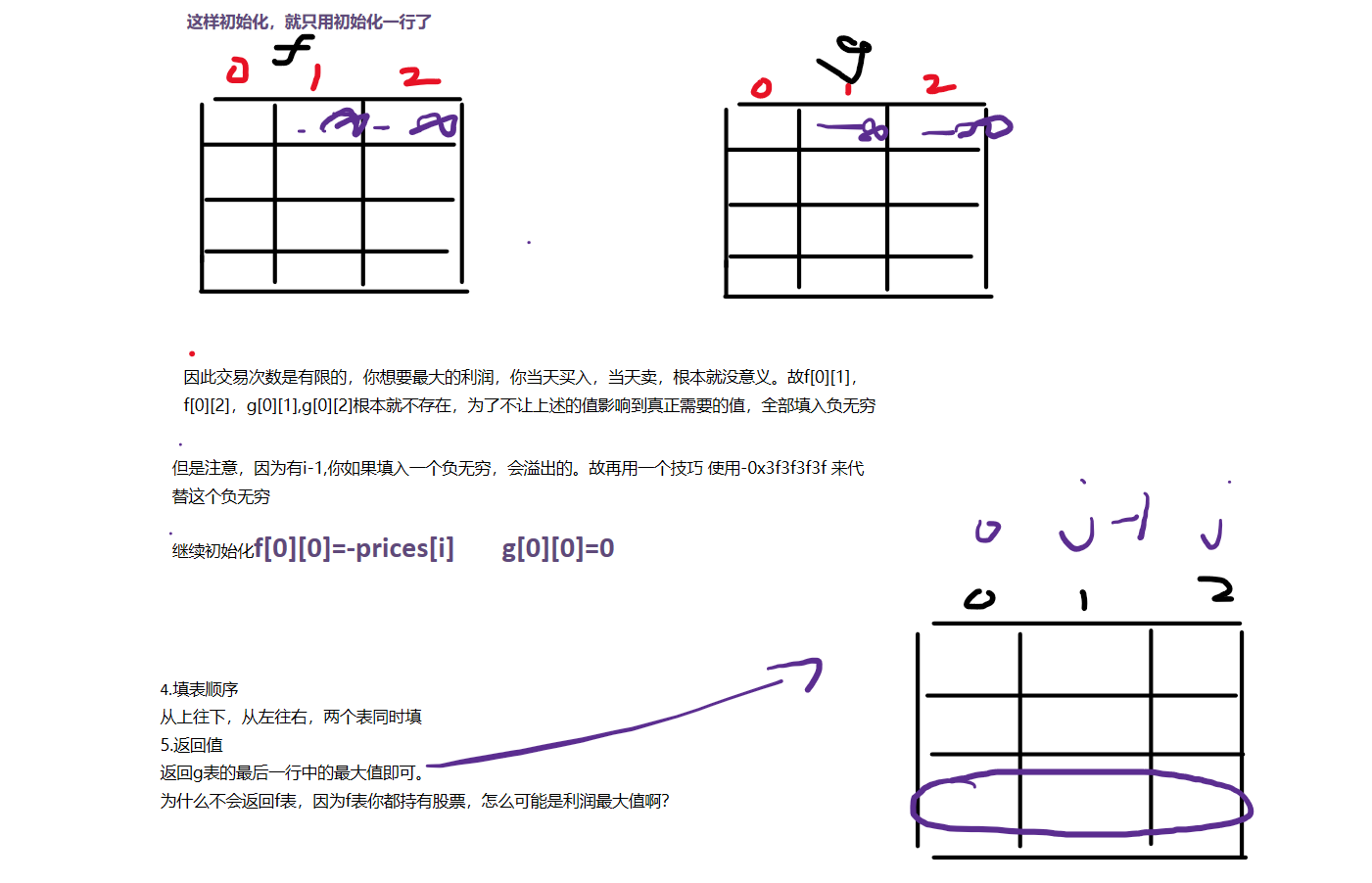
动态规划之买卖股票的最佳时机III代码实现

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        if(n==1){
            return 0;
        }
        boolean islow=true;
       for(int m=0;m=prices[m+1]){
            islow=true;
        }else{
            islow=false;
            break;
        }
       }
        if(islow==true){
            return 0;
        }
        int[][] f=new int[n][3];
        int[][] g=new int[n][3];
        f[0][0]=-prices[0];
        g[0][0]=0;
        f[0][1]=-0x3f3f3f3f;
        f[0][2]=-0x3f3f3f3f;
        g[0][1]=-0x3f3f3f3f;
        g[0][2]=-0x3f3f3f3f;
        for(int i=1;i=0){
                    g[i][j]=Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        return Math.max(g[n-1][0],Math.max(g[n-1][1],g[n-1][2]));
    }
}

简单分析一下动态规划之买卖股票的最佳时机IV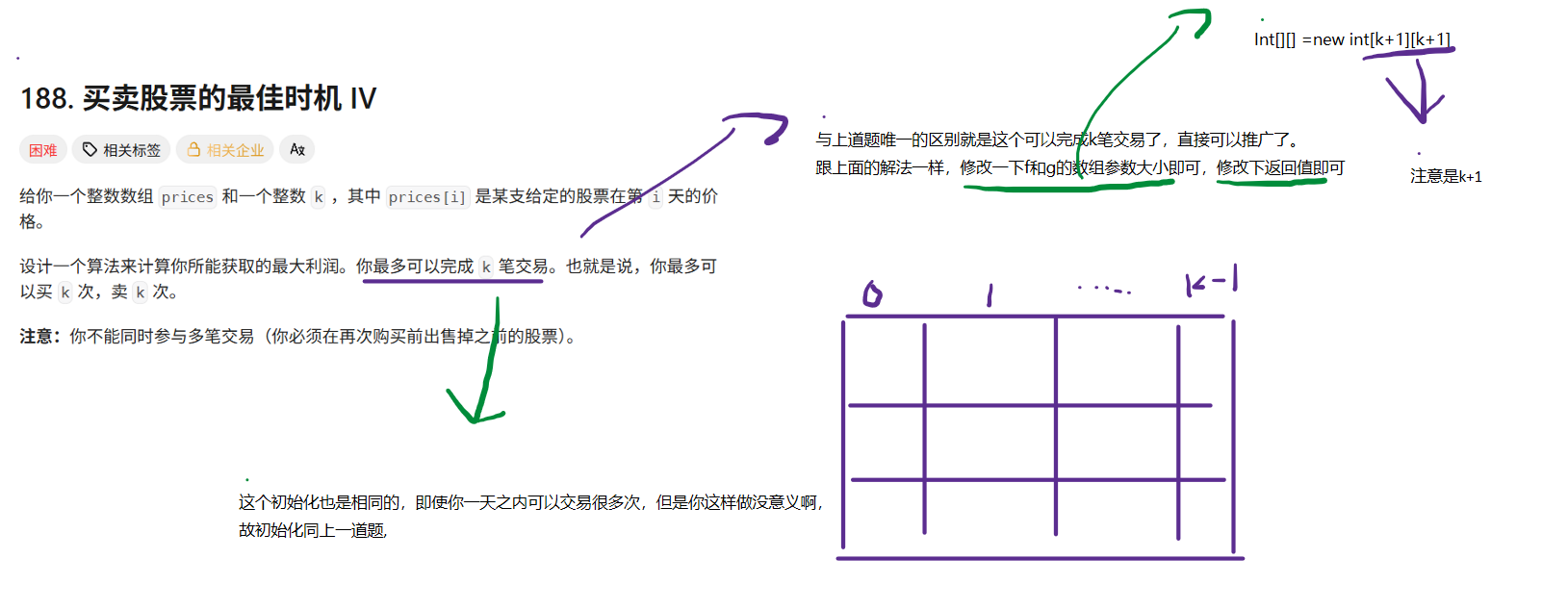

动态规划之买卖股票的最佳时机IV的代码实现

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n=prices.length;
        if(n==1){
            return 0;
        }
        boolean islow=true;
       for(int m=0;m=prices[m+1]){
            islow=true;
        }else{
            islow=false;
            break;
        }
       }
        if(islow==true){
            return 0;
        }
        //正如2次对应3
        //k对应k+1
        int[][] f=new int[n][k+1];
        int[][] g=new int[n][k+1];
        f[0][0]=-prices[0];
        g[0][0]=0;
        for(int j=1;j=0){
                    g[i][j]=Math.max(g[i-1][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        int max=0;
        for(int j=0;j=max){
                max=g[n-1][j];
            }
        }
        return max;
    }
}