数字信号处理 · 时域采样与频域采样 | 理论解析与实验验证 - 实践

注：本文为 “数字信号处理 · 时域采样与频域采样” 相关合辑。
略作重排，如有内容异常，请看原文。

---

时域采样定理和频域采样定理

yangyuwen_yang 于 2017-08-06 11:25:42 发布

采样定理的形象化描述

在时域对信号进行采样，等效于在频域对信号频谱进行周期延拓；在频域对频谱进行采样，等效于在时域对信号进行周期延拓。

时域采样定理（含带通采样定理）

对于一个频带有限的信号 $f(t)$，若其最高频率为 $f_m$，则该信号可唯一地由其在均匀间隔 $T_s$（采样间隔）上的样值点 $f(n{T}_s)$（其中 $n$ 为整数）恢复。实现信号唯一恢复的核心条件是：采样频率 $f_s=\frac{1}{T_s}$ 必须满足 $f_s>2f_m$，即采样间隔必须满足 $T_s<\frac{1}{2f_m}$。若不满足此条件，信号频谱会发生 混叠，导致无法从样值点准确重构原信号。

需指出，当 $T_s>\frac{1}{2f_m}$（即不满足无混叠采样条件）时，虽无法恢复原信号，但可通过滤波处理得到与原波形形态一致、但在时域上展宽的信号。这一特性在工程中具有实际应用，例如 取样示波器，其核心原理便是利用混叠效应，将难以直接显示的高频信号转化为易于观测的低频信号，实现对高频信号的间接测量。

频域采样定理

根据时域与频域的 对偶性（时域与频域的特性存在对称对应关系），可推导得出频域采样定理：对于一个时限信号 $f(t)$（即信号在时域区间 $(-t_m,t_m)$ 以外的取值均为 0），其频谱函数 $F(\mathrm{j}\omega )$ 可唯一地由其在均匀频率间隔 $\Delta f$（频率采样间隔）上的样值点 $F(\mathrm{j}n{\omega }_s)$（其中 $n$ 为整数，${\omega }_s=2\pi \Delta f$ 为角频率采样间隔）确定。实现频谱唯一确定的条件是：频率采样间隔需满足 $\Delta f<\frac{1}{2t_m}$。

从频域采样定理出发，可清晰建立 傅里叶变换 与 傅里叶级数 的内在联系：

1. 周期信号 $f_T(t)$ 的傅里叶系数，等于该周期信号单个周期内的信号 $f_0(t)$（即 $f_0(t)$ 仅在 $f_s(t)$ 的一个周期内与 $f_s(t)$ 取值相同，超出该周期时 $f_0(t)=0$）的傅里叶变换，在频域以数字角频率间隔 $n\Omega$（其中 $\Omega$ 为周期信号 $f_s(t)$ 的基波角频率）进行采样的结果；
2. 周期信号 $f_T(t)$ 的傅里叶变换，表现为以其傅里叶系数 $F_n$ 为相对模值的冲激序列，其数学表达式为：
   $$F(\mathrm{j}\omega )=2\pi \sum _{n=-\infty }^{\infty }{F}_n\delta (\omega -n\Omega )$$
   其中，$\delta (\cdot )$ 为冲激函数，仅在自变量为 0 时取值为无穷大，其余时刻取值为 0，用于表征周期信号频谱的离散冲激特性。

---

数字信号处理实验：时域采样与频域采样

Windsky_Yan 已于 2023-12-15 20:12:10 修改

实验内容

实验目的

时域采样理论与频域采样理论是数字信号处理中的重要理论。

本实验要求

• 掌握模拟信号采样前后频谱的变化，以及如何选择采样频率才能使采样后的信号不丢失信息；
• 掌握频率域采样会引起时域周期化的概念，以及频率域采样定理及其对频域采样点数选择的指导作用。

实验原理与方法

时域采样定理的要点是：

(1) 对模拟信号 $x_a(t)$ 以间隔 $T$ 进行时域等间隔理想采样，形成的采样信号的频谱 $\hat{X}(j\Omega )$ 是原模拟信号频谱 $X_a(j\Omega )$ 以采样角频率 ${\Omega }_s({\Omega }_s=2\pi /T)$ 为周期进行周期延拓。公式为：

$${\hat{X}}_a(j\Omega )=FT[\hat{x}(t)]=\frac{1}{T}\sum _{n=-\infty }^{\infty }{X}_a(j\Omega -jn{\Omega }_s)$$

采样频率 ${\Omega }_s$ 必须大于等于模拟信号最高频率的两倍以上，才能使采样信号的频谱不产生频谱混叠。

利用计算机计算上式并不方便，下面我们导出另外一个公式，以便用计算机上进行实验。理想采样信号 ${\hat{x}}_a(t)$ 和模拟信号 $x_a(t)$ 之间的关系为：

$${\hat{x}}_a(t)=x_a\sum _{n=-\infty }^{\infty }\delta (t-nT)$$

对上式进行傅里叶变换，得到：

$$\begin{array}{rl}{\hat{X}}_a(j\Omega )& ={\int }_{-\infty }^{\infty }[x_a(t)\sum _{n=\infty }^{\infty }\delta (t-nT)]e^{-j\Omega t}dt\\ & =\sum _{n=-\infty }^{\infty }{\int }_{-\infty }^{\infty }{x}_a(t)\delta (t-nT)e^{-j\Omega }dt\end{array}$$

在上式的积分号内只有当 $t=nT$ 时，才有非零值，因此：

$${\hat{X}}_a(j\Omega )=\sum _{n=-\infty }^{\infty }{x}_a(nT)e^{-j\Omega nT}$$

上式中，在数值上 $x_a(nT)=x(n)$，再将 $\omega =\Omega T$ 代入，得到：

$${\hat{X}}_a(j\Omega )=\sum _{n=-\infty }^{\infty }x(n)e^{-j\omega n}$$

上式的右边就是序列的傅立叶变换 $X(e^{j\omega })$，即

$${\hat{X}}_a(j\Omega )=X(e^{j\omega }){\mid }_{\omega =\Omega T}$$

上式说明理想采样信号的傅立叶变换可用相应的采样序列的傅立叶变换得到，只要将自变量 $\omega$ 用 $\Omega$ 代替即可。

频域采样定理的要点是：

对信号 $x(n)$ 的频谱函数 $X(e^{j\omega })$ 在 $[0,2\pi ]$ 上等间隔采样 $N$ 点，得到

$$X_N(k)=X(e^{j\omega }){\mid }_{\omega =\frac{2\pi }{N}}k=0,1,2,\dots ,N-1$$

则 $N$ 点 $IDFT[X_N(k)]$ 得到的序列就是原序列 $x(n)$ 以 $N$ 为周期进行周期延拓后的主值区序列，

公式为：

$$X_N(n)=IDFT[X_N(k){]}_N=[\sum _{i=\infty }^{\infty }x(n+iN)]R_N(n)$$

由上式可知，频域采样点数 $N$ 必须大于等于时域离散信号的长度 $M$（即 $N\ge M$），才能使时域不产生混叠，则 $N$ 点 $IDFT[X_N(k)]$ 得到的序列 $x_N(n)$ 就是原序列 $x(n)$，即 $X_n(n)=x(n)$。
如果 $N>M$，$x_N(n)$ 比原序列尾部多 $N-M$ 个零点；
如果 $N<M$，则 $x_N(n)=IDFT[X_N(k)]$ 发生了时域混叠失真，而且 $x_N(n)$ 的长度 $N$ 也比 $x(n)$ 的长度 $M$ 短。
因此，$x_N(n)$ 与 $x(n)$ 不相同。

在数字信号处理的应用中，只要涉及时域或者频域采样，都必须服从这两个采样理论的要点。

对比上面叙述的时域采样原理和频域采样原理，得到一个有用的结论，这两个采样理论具有对偶性：“时域采样频谱周期延拓，频域采样时域信号周期延拓”。因此放在一起进行实验。

实验内容及步骤

时域采样理论的验证

给定模拟信号

$$x_a=A{e}^{-at}\sin ({\Omega }_{0}t)u(t)$$

式中 $A=444.128$，$\alpha =50\sqrt{2}\pi$，${\Omega }_0=50\sqrt{2}\pi$ 它的幅频特性曲线如图所示。

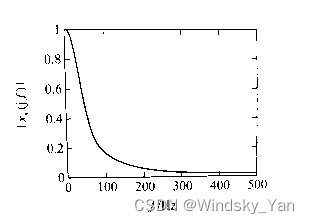
现用 DFT（FFT）求该模拟信号的幅频特性，以验证时域采样理论。

按照 $x_a(t)$ 的幅频特性曲线，选取三种采样频率，即 $F_s=1\text{kHz}$，300Hz，200Hz。观测时间选 $T_p=50\text{ms}$。

为使用 DFT，首先用下面公式产生时域离散信号，对三种采样频率，采样序列按顺序用 $x_1(n),x_2(n),x_3(n)$ 表示。

$$x(n)=x_a(nT)=A{e}^{-\alpha nT}\sin ({\Omega }_{0}nT)u(nT)$$

因为采样频率不同，得到的 $x_1(n),x_2(n),x_3(n)$ 的长度不同，长度（点数）用公式 $N=Y_p\times F_s$ 计算。选 FFT 的变换点数为 $M=64$，序列长度不够 64 的尾部加零。

$$X(k)=FFT[x(n)],k=0,1,2,\dots ,M-1$$

式中，$k$ 代表的频率为 ${\omega }_k=\frac{2\pi }{M}k$。

要求：编写实验程序，计算 $x_1(n),x_2(n),x_3(n)$ 的幅度特性，并绘图显示。观察分析频谱混叠失真。

频域采样理论的验证

给定信号如下：

$$x(n)=\{\begin{array}{ll}n+1& 0\le n\le 13\\ 27-n& 14\le n\le 26\\ 0& \text{其它}\end{array}$$

编写程序分别对频谱函数 $X(e^{j\omega })=FT[x(n)]$ 在区间 $[0,2\pi ]$ 上等间隔采样 32 点和 16 点，得到 $X_{32}(k)$ 和 $X_{16}(k)$：

$$\begin{gathered} X_{32}(k)=X(e^{j\omega }){\mid }_{\omega =\frac{2\pi }{32}k},k=0,1,2,\dots ,31 \\ {X}_{16}(k)=X(e^{j\omega }){\mid }_{\omega =\frac{2\pi }{16}k},k=0,1,2,\dots ,15 \end{gathered}$$

再分别对 $X_{32}(k)$ 和 $X_{16}(k)$ 进行 32 点和 16 点 IFFT，得到 $x_{32}(k)$ 和 $x_{16}(k)$：

$$\begin{gathered} x_{32}(n)=IFFT[X_{32}(k){]}_{32},n=0,1,2,\dots ,31 \\ {x}_{16}(n)=IFFT[X_{16}(k){]}_{16},n=0,1,2,\dots ,15 \end{gathered}$$

分别画出 $X(e^{j\omega })$、$X_{32}(k)$ 和 $X_{16}(k)$ 的幅度谱，并绘图显示 $x(n)$、$x_{32}(k)$ 和 $x_{16}(k)$ 的波形，进行对比和分析，验证总结频域采样理论。

提示：频域采样用以下方法容易变程序实现。

直接调用 MATLAB 函数 fft 计算 $X_{32}(k)=FFT[x(n){]}_{32}$ 就得到 $X(e^{j\omega })$ 在 $[0,2\pi ]$ 的 32 点频率域采样 $X_{32}(k)$。

抽取 $X_{32}(k)$ 的偶数点即可得到 $X(e^{j\omega })$ 在 $[0,2\pi ]$ 的 16 点频率域采样 $X_{16}(k)$，即 $X_{16}(k)=X_{32}(2k),k=0,1,2,\dots ,15$。

当然也可以按照频域采样理论，先将信号 $x(n)$ 以 16 为周期进行周期延拓，取其主值区（16 点），再对其进行 16 点 DFT（FFT），得到的就是 $X(e^{j\omega })$ 在 $[0,2\pi ]$ 的 16 点频率域采样 $X_{16}(k)$。

实验程序

%《数字信号处理(第4版）》第10章实验2程序exp2b.m
% 西安电子科技大学出版社出版  高西全  丁玉美 合著 2016年
% 频域采样理论验证
M = 27; N = 32; n = 0:M;
% 产生M长三角波序列x(n)
xa = 0:floor(M / 2); xb = ceil(M / 2) - 1:-1:0; xn = [xa, xb];
Xk = fft(xn, 1024); % 1024点FFT[x(n)],用于近似序列x(n)的TF
X32k = fft(xn, 32); % 32点FFT[x(n)]
x32n = ifft(X32k); % 32点IFFT[X32(k)]得到x32(n)
X16k = X32k(1:2:N); % 隔点抽取X32k得到X16(K)
x16n = ifft(X16k, N / 2); % 16点IFFT[X16(k)]得到x16(n)
subplot(3, 2, 2); stem(n, xn, '.'); box on
title('(b) 三角波序列x(n)'); xlabel('n'); ylabel('x(n)'); axis([0, 32, 0, 20])
k = 0:1023; wk = 2 * k / 1024;
subplot(3, 2, 1); plot(wk, abs(Xk)); title('(a)FT[x(n)]')
xlabel('\omega/\pi'); ylabel('|X(e^{j\omega})|'); axis([0, 1, 0, 200])
k = 0:N / 2 - 1;
subplot(3, 2, 3); stem(k, abs(X16k), '.'); box on
title('(c) 16点频域采样'); xlabel('k'); ylabel('|X_{16}(k)|'); axis([0, 8, 0, 200])
n1 = 0:N / 2 - 1;
subplot(3, 2, 4); stem(n1, x16n, '.'); box on
title('(d) 16点IDFT[X_{16}(k)]'); xlabel('n'); ylabel('x_{16}(n)'); axis([0, 32, 0, 20])
k = 0:N - 1;
subplot(3, 2, 5); stem(k, abs(X32k), '.'); box on
title('(e) 32点频域采样'); xlabel('k'); ylabel('|X_{32}(k)|'); axis([0, 16, 0, 200])
n1 = 0:N - 1;
subplot(3, 2, 6); stem(n1, x32n, '.'); box on
title('(f) 32点IDFT[X_{32}(k)]'); xlabel('n'); ylabel('x_{32}(n)'); axis([0, 32, 0, 20])

%《数字信号处理(第4版）》第10章实验2程序exp2a.m
% 西安电子科技大学出版社出版  高西全  丁玉美 合著 2016年
% 时域采样理论验证
Tp = 64 / 1000;
% 产生M长采样序列x(n)
Fs = 1000; T = 1 / Fs;
M = Tp * Fs; n = 0:M - 1;
A = 444.128; alph = pi * 50 * 2^0.5; omega = pi * 50 * 2^0.5;
xnt = A * exp(-alph * n * T) .* sin(omega * n * T);
Xk = T * fft(xnt, M); % M点FFT[xnt)]
yn = 'xa(nT)';
subplot(3, 2, 1); tstem(xnt, yn); box on; title('(a) Fs=1000Hz')
k = 0:M - 1; fk = k / Tp;
subplot(3, 2, 2); plot(fk, abs(Xk)); title('(a) T*FT[xa(nT)],Fs=1000Hz')
xlabel('f(Hz)')
ylabel('幅度'); axis([0, Fs, 0, 1.2 * max(abs(Xk))])
Fs = 300; T = 1 / Fs;
M = ceil(Tp * Fs); n = 0:M - 1;
xnt = A * exp(-alph * n * T) .* sin(omega * n * T);
Xk = T * fft(xnt, M); % M点FFT[xnt)]
yn = 'xa(nT)';
subplot(3, 2, 3); tstem(xnt, yn); box on; title('(b) Fs=300Hz')
k = 0:M - 1; fk = k / Tp;
subplot(3, 2, 4); plot(fk, abs(Xk)); title('(b) T*FT[xa(nT),Fs=300Hz')
xlabel('f(Hz)'); ylabel('幅度'); axis([0, Fs, 0, 1.2 * max(abs(Xk))])
Fs = 200; T = 1 / Fs;
M = ceil(Tp * Fs); n = 0:M - 1;
xnt = A * exp(-alph * n * T) .* sin(omega * n * T);
Xk = T * fft(xnt, M); % M点FFT[xnt)]
yn = 'xa(nT)';
subplot(3, 2, 5); tstem(xnt, yn); box on; title('(c) Fs=200Hz')
k = 0:M - 1; fk = k / Tp;
subplot(3, 2, 6); plot(fk, abs(Xk)); title('(c) T*FT[xa(nT),Fs=200Hz')
xlabel('f(Hz)'); ylabel('幅度'); axis([0, Fs, 0, 1.2 * max(abs(Xk))])

% 时域序列绘图函数
% xn:信号数据序列，yn:绘图信号的纵坐标名称（字符串）
function tstem(xn, yn)
n = 0:length(xn) - 1;
stem(n, xn, '.');
xlabel('n'); ylabel(yn);
axis([0, n(end), min(xn), 1.2 * max(xn)]);
end

实验结果

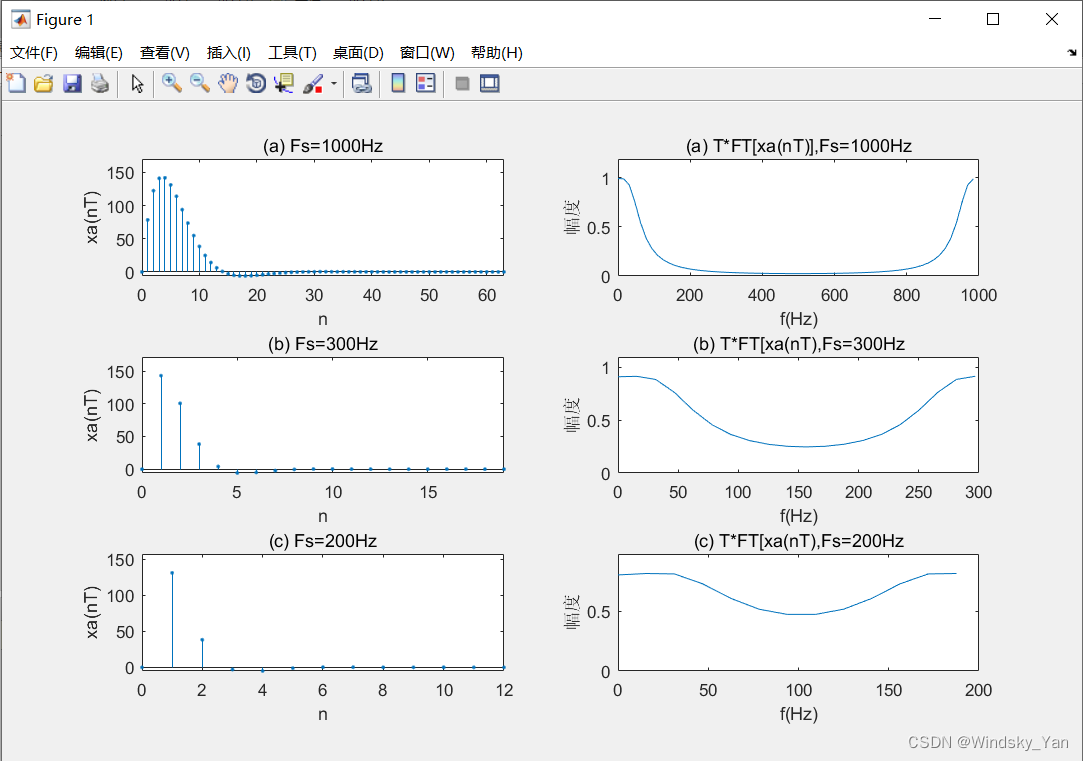
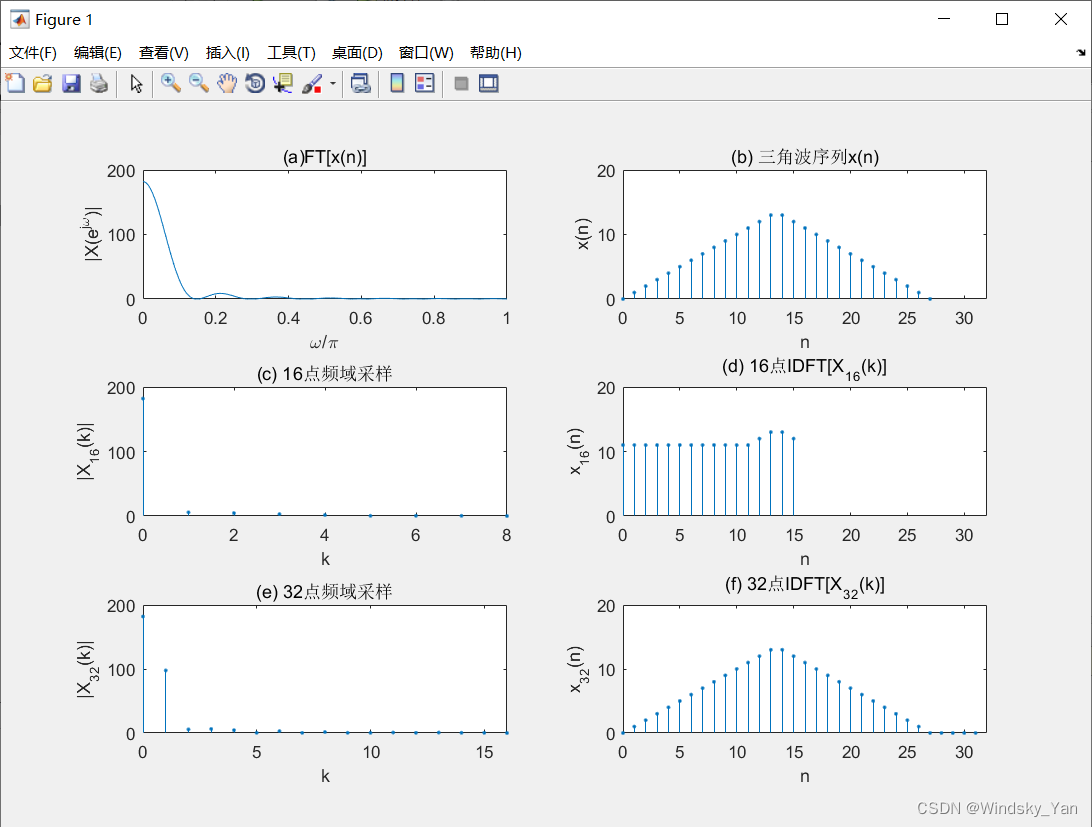
实验结果分析与实验总结

由图 1 可见，采样序列的频谱的确是以采样频率为周期对模拟信号频谱的周期延拓。
当采样频率为 1000 Hz 时，频谱混叠很小；
当采样频率为 300 Hz 时，在折叠频率 150 Hz 附近频谱混叠很严重；
当采样频率为 200 Hz 时，在折叠频率 100 Hz 附近频谱混叠更严重。

图 2 验证了频域采样理论和频域采样定理。对信号 $x(n)$ 的频谱函数 $X(e^{j\omega })$ 在 $[0,2\pi ]$ 上等间隔采样 $N=16$ 时，$N$ 点 $IDFT[X_N(k)]$ 得到的序列正是原序列 $x(n)$ 以 16 为周期进行周期延拓后的主值区序列：

$$X_N(n)=IDFT[X_N(k){]}_N=\left[\sum _{i=-\infty }^{\infty }x(n+iN)\right]R_N(n)$$

如图所示，
由于 $N<M$，所以发生了时域混叠失真，因此 $x_N(n)$ 与 $x(n)$ 不相同。
当 $N=32$ 时，由于 $N>M$，根据频域采样定理，不存在时域混叠失真。因此，$X_N(n)$ 与 $x(n)$ 相同。

• 若$N<M$，则不满足频域采样定理，时域混叠失真生，$x_N(n)$与$x(n)$相异；
• 若$N=32$（且$N>M$），则满足频域采样定理，时域混叠失真消，$x_N(n)$与$x(n)$相同。

---

via:

• 时域采样定理和频域采样定理-CSDN博客
  https://blog.csdn.net/yangyuwen_yang/article/details/76761305

• 数字信号处理实验二：时域采样与频域采样_时域采样定理和频域采样定理-CSDN博客
  https://blog.csdn.net/m0_69137195/article/details/134171335