线代一轮复习 - 教程
2025-10-03 12:05 tlnshuju 阅读(52) 评论(0) 收藏 举报文章目录
1、行列式
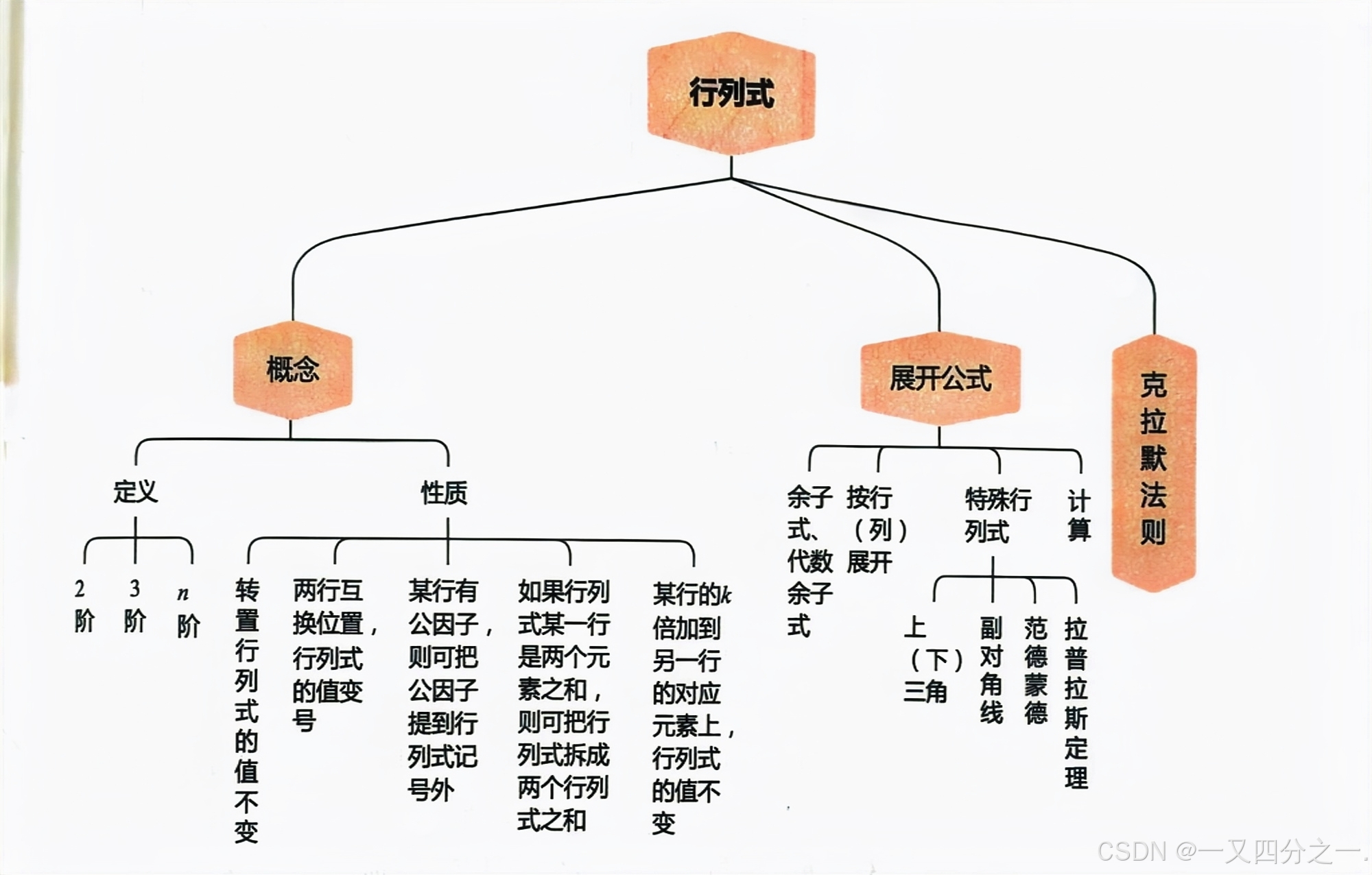
1.1 性质
转置性质
行列式转置后值不变:
∣ A T ∣ = ∣ A ∣ |A^T| = |A|∣AT∣=∣A∣行/列互换
两行(或列)互换,行列式变号。若两行(或列)相同,行列式为0。公因子提取
某行(或列)有公因子k kk,可提出:- 推论1:某行(或列)全为0,行列式为0。
- 推论2:两行(或列)成比例,行列式为0。
行列式拆分
若某行(或列)为两元素之和,可拆分为两个行列式之和:
∣ a 1 + b 1 ⋯ ⋮ ⋱ ∣ = ∣ a 1 ⋯ ⋮ ⋱ ∣ + ∣ b 1 ⋯ ⋮ ⋱ ∣ \begin{vmatrix}a_1+b_1 & \cdots \\\ \vdots & \ddots\end{vmatrix} = \begin{vmatrix}a_1 & \cdots \\\ \vdots & \ddots\end{vmatrix} + \begin{vmatrix}b_1 & \cdots \\\ \vdots & \ddots\end{vmatrix}a1+b1⋮⋯⋱=a1⋮⋯⋱+b1⋮⋯⋱倍加性质
某行(或列)的k kk倍加到另一行(或列),行列式值不变。
1.2 行列式展开公式
余子式与代数余子式
- 余子式M i j M_{ij}Mij:划去a i j a_{ij}aij所在行、列得到的( n − 1 ) (n-1)(n−1)阶行列式。
- 代数余子式A i j = ( − 1 ) i + j M i j A_{ij} = (-1)^{i+j}M_{ij}Aij=(−1)i+jMij。
展开定理
定理1.1:行列式可按任意行(列)展开:
∣ A ∣ = ∑ k = 1 n a i k A i k (按第 i 行展开) |A| = \sum_{k=1}^n a_{ik}A_{ik} \quad \text{(按第$i$行展开)}∣A∣=k=1∑naikAik(按第i行展开)∣ A ∣ = ∑ k = 1 n a k j A k j (按第 j 列展开) |A| = \sum_{k=1}^n a_{kj}A_{kj} \quad \text{(按第$j$列展开)}∣A∣=k=1∑nakjAkj(按第j列展开)
定理1.2:不同行(列)的代数余子式乘积和为0:
∑ k = 1 n a i k A j k = 0 ( i ≠ j ) \sum_{k=1}^n a_{ik}A_{jk} = 0 \quad (i \ne j)k=1∑naikAjk=0(i=j)
1.3 特殊行列式
- 三角形行列式
上(下)三角行列式等于主对角线元素乘积:
∣ a 11 ⋯ a 1 n ⋱ ⋮ 0 a n n ∣ = a 11 a 22 ⋯ a n n \begin{vmatrix}a_{11} & \cdots & a_{1n} \\\ & \ddots & \vdots \\\ 0 & & a_{nn}\end{vmatrix} = a_{11}a_{22}\cdots a_{nn}a110⋯⋱a1n⋮ann=a11a22⋯ann
- 副对角线行列式
∣ 0 ⋯ a 1 n ⋮ ⋱ ⋮ a n 1 ⋯ 0 ∣ = ( − 1 ) n ( n − 1 ) 2 a 1 n a 2 , n − 1 ⋯ a n 1 \begin{vmatrix}0 & \cdots & a_{1n} \\\ \vdots & \ddots & \vdots \\\ a_{n1} & \cdots & 0\end{vmatrix} = (-1)^{\frac{n(n-1)}{2}} a_{1n}a_{2,n-1}\cdots a_{n1}0⋮an1⋯⋱⋯a1n⋮0=(−1)2n(n−1)a1na2,n−1⋯an1
- 分块行列式(拉普拉斯展开)
若A AA为m mm阶,B BB为n nn阶矩阵:
∣ A ∗ O B ∣ = ∣ A ∣ ⋅ ∣ B ∣ \begin{vmatrix}A & * \\\ O & B\end{vmatrix} = |A|\cdot|B|AO∗B=∣A∣⋅∣B∣∣ O A B ∗ ∣ = ( − 1 ) m n ∣ A ∣ ⋅ ∣ B ∣ \begin{vmatrix}O & A \\\ B & *\end{vmatrix} = (-1)^{mn}|A|\cdot|B|OBA∗=(−1)mn∣A∣⋅∣B∣
- 范德蒙行列式
∣ 1 ⋯ 1 x 1 ⋯ x n ⋮ ⋱ ⋮ x 1 n − 1 ⋯ x n n − 1 ∣ = ∏ 1 ≤ j < i ≤ n ( x i − x j ) \begin{vmatrix}1 & \cdots & 1 \\\ x_1 & \cdots & x_n \\\ \vdots & \ddots & \vdots \\\ x_1^{n-1} & \cdots & x_n^{n-1}\end{vmatrix} = \prod_{1 \leq j < i \leq n} (x_i - x_j)1x1⋮x1n−1⋯⋯⋱⋯1xn⋮xnn−1=1≤j<i≤n∏(xi−xj)
注:
1.4 克拉默法则
定理1.3(克拉默法则)
对于由 ( n ) 个方程、( n ) 个未知量构成的非齐次线性方程组:
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 , a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 , ⋮ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1, \\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2, \\\ \vdots \\\\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n \end{cases}⎩⎨⎧a11x1+a12x2+⋯+a1nxn=b1,a21x1+a22x2+⋯+a2nxn=b2,⋮an1x1+an2x2+⋯+annxn=bn
若其系数行列式 (∣ A ∣ ≠ 0 |A| \neq 0∣A∣=0),则方程组有唯一解:
x i = ∣ A i ∣ ∣ A ∣ , i = 1 , 2 , ⋯ , n x_i = \frac{|A_i|}{|A|}, \quad i = 1, 2, \cdots, nxi=∣A∣∣Ai∣,i=1,2,⋯,n
其中 (∣ A i ∣ |A_i|∣Ai∣) 是将 ( ∣ A ∣ ( |A|(∣A∣) 的第 (i ii) 列替换为常数项 (b 1 , b 2 , ⋯ , b n b_1, b_2, \cdots, b_nb1,b2,⋯,bn) 所得的行列式。
注:
- 唯一解条件:仅当 (∣ A ∣ ≠ 0 |A| \neq 0∣A∣=0) 时适用。
- 特殊情况:
- 若 ( $|A| = 0 $),方程组可能无解或有无穷多解,但不可能有唯一解。
推论(齐次线性方程组)
对于齐次线性方程组(常数项全为0):
- 若 ( ∣ A ∣ ≠ 0 |A| \neq 0∣A∣=0),方程组仅有零解 (x 1 = x 2 = ⋯ = x n = 0 x_1 = x_2 = \cdots = x_n = 0x1=x2=⋯=xn=0)。
- 若 (∣ A ∣ = 0 |A| = 0∣A∣=0),方程组存在非零解(无穷多解)。
2、矩阵
2.1 矩阵多项式
2.2 运算法则
(1) 加法
设 A AA, B BB, C CC为同型矩阵,则:
- 交换律:A + B = B + A A + B = B + AA+B=B+A
- 结合律:( A + B ) + C = A + ( B + C ) (A + B) + C = A + (B + C)(A+B)+C=A+(B+C)
- 零矩阵:A + O = A A + O = AA+O=A(O OO为同型零矩阵)
- 负矩阵:A + ( − A ) = O A + (-A) = OA+(−A)=O
(2) 数乘矩阵
设 k kk, m mm为标量,则:
- 结合性:k ( m A ) = ( k m ) A = m ( k A ) k(mA) = (km)A = m(kA)k(mA)=(km)A=m(kA)
- 分配律:( k + m ) A = k A + m A (k + m)A = kA + mA(k+m)A=kA+mA
- 线性性:k ( A + B ) = k A + k B k(A + B) = kA + kBk(A+B)=kA+kB
- 单位数乘:1 A = A 1A = A1A=A, 0 A = O 0A = O0A=O
(3) 乘法
若矩阵 A AA, B BB, C CC满足乘法条件,则:
- 结合律:( A B ) C = A ( B C ) (AB)C = A(BC)(AB)C=A(BC)
- 左分配律:A ( B + C ) = A B + A C A(B + C) = AB + ACA(B+C)=AB+AC
- 右分配律:( B + C ) A = B A + C A (B + C)A = BA + CA(B+C)A=BA+CA
(4) 转置
- 和的转置:( A + B ) T = A T + B T (A + B)^T = A^T + B^T(A+B)T=AT+BT
- 数乘转置:( k A ) T = k A T (kA)^T = kA^T(kA)T=kAT
- 积的转置:( A B ) T = B T A T (AB)^T = B^T A^T(AB)T=BTAT
- 转置的转置:( A T ) T = A (A^T)^T = A(AT)T=A
注:矩阵乘法一般不满足交换律(即A B ≠ B A AB \neq BAAB=BA)。
2.3 对角矩阵的性质与运算
对角矩阵乘法
两个对角矩阵相乘结果仍为对角矩阵,且元素为对应位置相乘:
[ a 1 0 0 0 a 2 0 0 0 a 3 ] [ b 1 0 0 0 b 2 0 0 0 b 3 ] = [ a 1 b 1 0 0 0 a 2 b 2 0 0 0 a 3 b 3 ] \begin{bmatrix} a_1 & 0 & 0 \\\\ 0 & a_2 & 0 \\\\ 0 & 0 & a_3 \end{bmatrix} \begin{bmatrix} b_1 & 0 & 0 \\\\ 0 & b_2 & 0 \\\\ 0 & 0 & b_3 \end{bmatrix} = \begin{bmatrix} a_1 b_1 & 0 & 0 \\\\ 0 & a_2 b_2 & 0 \\\\ 0 & 0 & a_3 b_3 \end{bmatrix}a1000a2000a3b1000b2000b3=a1b1000a2b2000a3b3
性质
交换律
对角矩阵乘法可交换:Λ 1 Λ 2 = Λ 2 Λ 1 \Lambda_1 \Lambda_2 = \Lambda_2 \Lambda_1Λ1Λ2=Λ2Λ1。逆矩阵
若对角元素均非零(a i ≠ 0 a_i \neq 0ai=0),其逆矩阵为元素取倒数:
[ a 1 0 0 0 a 2 0 0 0 a 3 ] − 1 = [ 1 a 1 0 0 0 1 a 2 0 0 0 1 a 3 ] \begin{bmatrix} a_1 & 0 & 0 \\\\ 0 & a_2 & 0 \\\\ 0 & 0 & a_3 \end{bmatrix}^{-1} = \begin{bmatrix} \frac{1}{a_1} & 0 & 0 \\\\ 0 & \frac{1}{a_2} & 0 \\\\ 0 & 0 & \frac{1}{a_3} \end{bmatrix}a1000a2000a3−1=a11000a21000a31
2.4 伴随矩阵
设 A AA 是一个 n nn 阶方阵(n ≥ 2 n \geq 2n≥2),其伴随矩阵A ∗ A^*A∗(或记作 adj ( A ) \text{adj}(A)adj(A))定义为:
A ∗ = [ A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋱ ⋮ A 1 n A 2 n ⋯ A n n ] A^* = \begin{bmatrix} A_{11} & A_{21} & \cdots & A_{n1} \\\\ A_{12} & A_{22} & \cdots & A_{n2} \\\\ \vdots & \vdots & \ddots & \vdots \\\\ A_{1n} & A_{2n} & \cdots & A_{nn} \end{bmatrix}A∗=A11A12⋮A1nA21A22⋮A2n⋯⋯⋱⋯An1An2⋮Ann
其中 A i j A_{ij}Aij 是矩阵 A AA 的元素 a i j a_{ij}aij 的代数余子式(Cofactor),即:
A i j = ( − 1 ) i + j M i j , A_{ij} = (-1)^{i+j} M_{ij},Aij=(−1)i+jMij,
M i j M_{ij}Mij 是 A AA 删去第 i ii 行第 j jj 列后得到的 ( n − 1 ) (n-1)(n−1)阶子矩阵的行列式。
伴随矩阵的公式:
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^*A = |A|EAA∗=A∗A=∣A∣E
( A ∗ ) − 1 = ( A − 1 ) ∗ = 1 ∣ A ∣ A (A^*)^{-1} = (A^{-1})^* = \frac{1}{|A|}A(A∗)−1=(A−1)∗=∣A∣1A (∣ A ∣ ≠ 0 |A|\neq 0∣A∣=0)
( k A ) ∗ = k n − 1 A ∗ (kA)^* = k^{n-1}A^*(kA)∗=kn−1A∗
( A ∗ ) ⊤ = ( A ⊤ ) ∗ (A^*)^{\top} = (A^{\top})^*(A∗)⊤=(A⊤)∗
∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*| = |A|^{n-1}∣A∗∣=∣A∣n−1
( A ∗ ) ∗ = ∣ A ∣ n − 2 A (A^*)^* = |A|^{n-2}A(A∗)∗=∣A∣n−2A (n ≥ 2 n \geq 2n≥2)
2.4 可逆矩阵的概念与定理
定义 设 A AA 是 n nn阶矩阵,要是存在n nn 阶矩阵 B BB 使得
A B = B A = E AB = BA = EAB=BA=E(单位矩阵)
成立,则称 A AA 是可逆矩阵或非奇异矩阵,B BB 是 A AA的逆矩阵,记成A − 1 = B A^{-1} = BA−1=B。
定理 2.1 若 A AA 可逆,则 A AA的逆矩阵唯一。
定理 2.2A AA 可逆 ⇔ \Leftrightarrow⇔∣ A ∣ ≠ 0 |A| \neq 0∣A∣=0。
定理 2.3 设 A AA 和 B BB 是 n nn 阶矩阵且 A B = E AB = EAB=E,则 B A = E BA = EBA=E。
3. n nn 阶矩阵 A AA可逆的充分必要条件
- 存在 n nn 阶矩阵 B BB,使 A B = E AB = EAB=E(或 B A = E BA = EBA=E)
- ∣ A ∣ ≠ 0 |A| \neq 0∣A∣=0,或秩 r ( A ) = n r(A) = nr(A)=n,或 A AA的列(行)向量线性无关
- 齐次方程组 A x = 0 Ax = 0Ax=0 只有零解
- ∀ b \forall b∀b,非齐次线性方程组A x = b Ax = bAx=b 总有唯一解
- 矩阵 A AA的特征值全不为 0
4. 逆矩阵的运算性质
若 k ≠ 0 k \neq 0k=0, A AA 可逆,则 ( k A ) − 1 = 1 k A − 1 (kA)^{-1} = \frac{1}{k}A^{-1}(kA)−1=k1A−1。
若 A , B A, BA,B 可逆,则 ( A B ) − 1 = B − 1 A − 1 (AB)^{-1} = B^{-1}A^{-1}(AB)−1=B−1A−1,特别地 ( A 2 ) − 1 = ( A − 1 ) 2 (A^2)^{-1} = (A^{-1})^2(A2)−1=(A−1)2。
若 A ⊤ A^{\top}A⊤ 可逆,则 ( A ⊤ ) − 1 = ( A − 1 ) ⊤ (A^{\top})^{-1} = (A^{-1})^{\top}(A⊤)−1=(A−1)⊤;( A − 1 ) − 1 = A (A^{-1})^{-1} = A(A−1)−1=A;∣ A − 1 ∣ = 1 ∣ A ∣ |A^{-1}| = \frac{1}{|A|}∣A−1∣=∣A∣1。
注意 即使 A , B A, BA,B 和 A + B A + BA+B都可逆,一般地( A + B ) − 1 ≠ A − 1 + B − 1 (A + B)^{-1} \neq A^{-1} + B^{-1}(A+B)−1=A−1+B−1。
5. 求逆矩阵的方法
方法一 用公式,若 ∣ A ∣ ≠ 0 |A|\neq0∣A∣=0,则 A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{|A|}A^*A−1=∣A∣1A∗。
方法二初等变换法。( A : E ) → 初等行变换 ( E : A − 1 ) (A:E) \xrightarrow{\text{初等行变换}} (E:A^{-1})(A:E)初等行变换(E:A−1)。
方法三 用定义求 B BB,使 A B = E AB=EAB=E 或 B A = E BA=EBA=E,则 A AA 可逆,且 A − 1 = B A^{-1}=BA−1=B。
方法四用分块矩阵。
设 B , C B,CB,C都是可逆矩阵,则
[ B O O C ] − 1 = [ B − 1 O O C − 1 ] , [ O B C O ] − 1 = [ O C − 1 B − 1 O ] \begin{bmatrix} B & O \\\\ O & C \end{bmatrix}^{-1} = \begin{bmatrix} B^{-1} & O \\\\ O & C^{-1} \end{bmatrix}, \begin{bmatrix} O & B \\\\ C & O \end{bmatrix}^{-1} = \begin{bmatrix} O & C^{-1} \\\\ B^{-1} & O \end{bmatrix}BOOC−1=B−1OOC−1,OCBO−1=OB−1C−1O
3、向量
3.1线性组合和线性表示
- 给定向量组 A : a 1 , a 2 , a 3 , . . . , a m A:a_1,a_2,a_3,...,a_mA:a1,a2,a3,...,am,对于任何一组实数k 1 , k 2 , k 3 , . . . , k m k_1,k_2,k_3,...,k_mk1,k2,k3,...,km,表达式 k 1 a 1 + k 2 a 2 + k 3 a 3 + ⋅ ⋅ ⋅ + k m a m k_1a_1+k_2a_2+k_3a_3+···+k_ma_mk1a1+k2a2+k3a3+⋅⋅⋅+kmam 称为向量组 A 的一个线性组合,k 1 , k 2 , k 3 , . . . , K m k_1,k_2,k_3,...,K_mk1,k2,k3,...,Km称为这个线性组合的系数
- 给定向量组 A : a 1 , a 2 , a 3 , . . . , a m A:a_1,a_2,a_3,...,a_mA:a1,a2,a3,...,am,向量 b bb,如果存在一组数λ 1 , λ 2 , λ 3 , ⋅ ⋅ ⋅ , λ m λ_1,λ_2,λ_3,···,λ_mλ1,λ2,λ3,⋅⋅⋅,λm,使 b = λ 1 a 1 + λ 2 a 2 + λ 3 a 3 + ⋅ ⋅ ⋅ + λ m a m b=λ_1a_1+λ_2a_2+λ_3a_3+···+λ_ma_mb=λ1a1+λ2a2+λ3a3+⋅⋅⋅+λmam ,则向量 b 是向量组 A的线性组合,这时称向量 b 能由向量组 A 线性表示
定理:
- 向量 b bb 由向量组 A : a 1 , a 2 , a 3 , . . . , a m A:a_1,a_2,a_3,...,a_mA:a1,a2,a3,...,am矩阵就是表示的充分必要条件A = ( a 1 , a 2 , a 3 , ⋅ ⋅ ⋅ , a m ) A=(a_1,a_2,a_3,···,a_m)A=(a1,a2,a3,⋅⋅⋅,am)的秩等于矩阵B = ( a 1 , a 2 , a 3 , . . . , a m , b ) B=(a_1,a_2,a_3,...,a_m,b)B=(a1,a2,a3,...,am,b) 的秩
- 若 A ,B能互相表示,则称他们是等价的
- 向量组 A 能由向量组 B线性表示的充分必要条件为R ( A ) = R ( A , B ) R(A)=R(A,B)R(A)=R(A,B),或者R ( A ) ≤ R ( B ) R(A) ≤ R(B)R(A)≤R(B),等价的充要条件为 R ( A ) = R ( B ) = R ( A , B ) R(A)=R(B)=R(A,B)R(A)=R(B)=R(A,B)
3.2 线性相关与线性无关
- 给定向量组 A : a 1 , a 2 , a 3 , . . . , a m A:a_1,a_2,a_3,...,a_mA:a1,a2,a3,...,am,存在不全为零实数k 1 , k 2 , k 3 , . . . , k m k_1,k_2,k_3,...,k_mk1,k2,k3,...,km,使 k 1 a 1 + k 2 a 2 + k 3 a 3 + ⋅ ⋅ ⋅ + k m a m = 0 k_1a_1+k_2a_2+k_3a_3+···+k_ma_m = 0k1a1+k2a2+k3a3+⋅⋅⋅+kmam=0,则称向量组 A 是线性相关的,否则称他线性无关
简单来说:
- 线性相关:有非零解
- 线性无关:只有零解
重要结论:
- 方阵形式:直接判断行列式的值是否为零,线性相关D为0,线性无关D不为0
- 行数大于列数的矩阵:判断齐次线性方程组的解,线性相关有非零解,线性无关只有零解
- 列数大于行数的矩阵:向量个数大于维数,一定线性相关
向量组 a 1 , a 2 , a 3 , . . . , a m a_1,a_2,a_3,...,a_ma1,a2,a3,...,am线性相关:其中就是的充分必要条件至少有一个向量可由其余 m -1 个向量线性表示
向量组 a 1 , a 2 , a 3 , . . . , a m a_1,a_2,a_3,...,a_ma1,a2,a3,...,am线性无关的充分必要条件是:其中每一个向量都不能由其余 m -1 个向量线性表示
若向量组 a 1 , a 2 , a 3 , . . . , a m a_1,a_2,a_3,...,a_ma1,a2,a3,...,am线性无关,而向量组a 1 , a 2 , a 3 , . . . , a m , b a_1,a_2,a_3,...,a_m,ba1,a2,a3,...,am,b 线性相关,则 b 可由a 1 , a 2 , a 3 , . . . , a m a_1,a_2,a_3,...,a_ma1,a2,a3,...,am线性表示,且表达式唯一
注:线性表示和线性相关性是不同的概念
- 若部分线性相关,则整个向量组也线性相关
- 若整体线性无关,则任意一个部分也线性无关
- 如果n维向量组a 1 , a 2 , a 3 , . . . , a m a_1,a_2,a_3,...,a_ma1,a2,a3,...,am线性无关,则在每一个向量上都添加 m 个分量,得到的n+m 维接长的向量组也线性无关
- 如果n维向量组a 1 , a 2 , a 3 , . . . , a m a_1,a_2,a_3,...,a_ma1,a2,a3,...,am线性相关,则在每一个向量上都减去 m 个分量,得到的n-m 维截断的向量组也线性相关
- 向量组线性无关 ⇔ 秩等于向量个数
- 线性相关 ⇔ 秩小于向量个数
3.3 向量组的秩
定义:向量组的极大无关组所包含向量的个数,称为向量组的的秩
定理:
- 假设两个向量组的秩相等,且其中一个向量组可由另一个线性表示,则两个向量组等价
行向量组与列向量组:
- 行向量组的秩为行秩,列向量组的秩为列秩
- 行秩=列秩=矩阵的秩
3.4 极大无关组
定义:设向量组A : a 1 , a 2 , a 3 , . . . , a m A:a_1,a_2,a_3,...,a_mA:a1,a2,a3,...,am中有一部分向量组a 1 , a 2 , a 3 , . . . , a r ( r < n ) a_1,a_2,a_3,...,a_r (r<n)a1,a2,a3,...,ar(r<n)满足
- $a_1,a_2,a_3,…,a_r $线性无关
- 向量组 A 中任意r + 1 r+1r+1(如果有 r + 1 r+1r+1个向量的话) ,则称a 1 , a 2 , a 3 , . . . , a r a_1,a_2,a_3,...,a_ra1,a2,a3,...,ar是向量组 A 的一个极大线性无关组。简称为极大无关组
3.5 内积
3.5.1 定义与性质
内积定义:对于向量a = ( a 1 , . . . , a n ) \mathbf{a}=(a_1,...,a_n)a=(a1,...,an)和b = ( b 1 , . . . , b n ) \mathbf{b}=(b_1,...,b_n)b=(b1,...,bn),其内积为:
[ a , b ] = ∑ i = 1 n a i b i [\mathbf{a},\mathbf{b}] = \sum_{i=1}^n a_ib_i[a,b]=i=1∑naibi矩阵内积:对于m × n m×nm×n矩阵A , B A,BA,B,其内积为:
[ A , B ] = ∑ i = 1 m ∑ j = 1 n a i j b i j [A,B] = \sum_{i=1}^m\sum_{j=1}^n a_{ij}b_{ij}[A,B]=i=1∑mj=1∑naijbij向量长度(范数):
∥ a ∥ = [ a , a ] = ∑ i = 1 n a i 2 \|\mathbf{a}\| = \sqrt{[\mathbf{a},\mathbf{a}]} = \sqrt{\sum_{i=1}^n a_i^2}∥a∥=[a,a]=i=1∑nai2单位向量:若∥ a ∥ = 1 \|\mathbf{a}\|=1∥a∥=1,则称a \mathbf{a}a为单位向量
施瓦茨不等式:
∣ [ a , b ] ∣ ≤ ∥ a ∥ ⋅ ∥ b ∥ |[\mathbf{a},\mathbf{b}]| \leq \|\mathbf{a}\|\cdot\|\mathbf{b}\|∣[a,b]∣≤∥a∥⋅∥b∥
3.5.2 重要性质
- 对称性:[ a , b ] = [ b , a ] [\mathbf{a},\mathbf{b}]=[\mathbf{b},\mathbf{a}][a,b]=[b,a]
- 线性性:[ k a + b , c ] = k [ a , c ] + [ b , c ] [k\mathbf{a}+\mathbf{b},\mathbf{c}]=k[\mathbf{a},\mathbf{c}]+[\mathbf{b},\mathbf{c}][ka+b,c]=k[a,c]+[b,c]
- 正定性:[ a , a ] ≥ 0 [\mathbf{a},\mathbf{a}] \geq 0[a,a]≥0,且[ a , a ] = 0 ⟺ a = 0 [\mathbf{a},\mathbf{a}]=0 \iff \mathbf{a}=\mathbf{0}[a,a]=0⟺a=0
例题1:计算向量a = ( 1 , 2 , 3 ) \mathbf{a}=(1,2,3)a=(1,2,3)和b = ( 4 , − 5 , 6 ) \mathbf{b}=(4,-5,6)b=(4,−5,6)的内积和长度。
解:
内积:
[ a , b ] = 1 × 4 + 2 × ( − 5 ) + 3 × 6 = 4 − 10 + 18 = 12 [\mathbf{a},\mathbf{b}] = 1×4 + 2×(-5) + 3×6 = 4-10+18=12[a,b]=1×4+2×(−5)+3×6=4−10+18=12长度:
∥ a ∥ = 1 2 + 2 2 + 3 2 = 14 \|\mathbf{a}\| = \sqrt{1^2+2^2+3^2} = \sqrt{14}∥a∥=12+22+32=14
∥ b ∥ = 4 2 + ( − 5 ) 2 + 6 2 = 77 \|\mathbf{b}\| = \sqrt{4^2+(-5)^2+6^2} = \sqrt{77}∥b∥=42+(−5)2+62=77
3.6 正交向量组
3.6.1 基本概念
- 正交定义:若[ a , b ] = 0 [\mathbf{a},\mathbf{b}]=0[a,b]=0,则称向量a \mathbf{a}a与b \mathbf{b}b正交
- 正交向量组:由非零向量组成的向量组,其中任意两个不同向量都正交
- 标准正交基:由单位向量组成的正交向量组
3.6.2 重要定理
正交向量组的线性无关性:
任何正交向量组都是线性无关的Gram-Schmidt正交化:
可将线性无关向量组转化为正交向量组:- b 1 = a 1 \mathbf{b}_1 = \mathbf{a}_1b1=a1
- b 2 = a 2 − [ a 2 , b 1 ] [ b 1 , b 1 ] b 1 \mathbf{b}_2 = \mathbf{a}_2 - \frac{[\mathbf{a}_2,\mathbf{b}_1]}{[\mathbf{b}_1,\mathbf{b}_1]}\mathbf{b}_1b2=a2−[b1,b1][a2,b1]b1
- b 3 = a 3 − [ a 3 , b 1 ] [ b 1 , b 1 ] b 1 − [ a 3 , b 2 ] [ b 2 , b 2 ] b 2 \mathbf{b}_3 = \mathbf{a}_3 - \frac{[\mathbf{a}_3,\mathbf{b}_1]}{[\mathbf{b}_1,\mathbf{b}_1]}\mathbf{b}_1 - \frac{[\mathbf{a}_3,\mathbf{b}_2]}{[\mathbf{b}_2,\mathbf{b}_2]}\mathbf{b}_2b3=a3−[b1,b1][a3,b1]b1−[b2,b2][a3,b2]b2
- …
例题2:验证向量组a 1 = ( 1 , 1 , 1 ) \mathbf{a}_1=(1,1,1)a1=(1,1,1),a 2 = ( 1 , − 1 , 0 ) \mathbf{a}_2=(1,-1,0)a2=(1,−1,0),a 3 = ( 1 , 1 , − 2 ) \mathbf{a}_3=(1,1,-2)a3=(1,1,−2)是否正交。
解:
计算各对内积:
- [ a 1 , a 2 ] = 1 × 1 + 1 × ( − 1 ) + 1 × 0 = 0 [\mathbf{a}_1,\mathbf{a}_2] = 1×1 + 1×(-1) + 1×0 = 0[a1,a2]=1×1+1×(−1)+1×0=0
- [ a 1 , a 3 ] = 1 × 1 + 1 × 1 + 1 × ( − 2 ) = 0 [\mathbf{a}_1,\mathbf{a}_3] = 1×1 + 1×1 + 1×(-2) = 0[a1,a3]=1×1+1×1+1×(−2)=0
- [ a 2 , a 3 ] = 1 × 1 + ( − 1 ) × 1 + 0 × ( − 2 ) = 0 [\mathbf{a}_2,\mathbf{a}_3] = 1×1 + (-1)×1 + 0×(-2) = 0[a2,a3]=1×1+(−1)×1+0×(−2)=0
因此该向量组是正交向量组。
例题3:将线性无关向量组a 1 = ( 1 , 1 , 0 ) \mathbf{a}_1=(1,1,0)a1=(1,1,0),a 2 = ( 1 , 0 , 1 ) \mathbf{a}_2=(1,0,1)a2=(1,0,1),a 3 = ( 0 , 1 , 1 ) \mathbf{a}_3=(0,1,1)a3=(0,1,1)正交化。
解:
使用Gram-Schmidt正交化:
- b 1 = a 1 = ( 1 , 1 , 0 ) \mathbf{b}_1 = \mathbf{a}_1 = (1,1,0)b1=a1=(1,1,0)
- b 2 = a 2 − [ a 2 , b 1 ] [ b 1 , b 1 ] b 1 = ( 1 , 0 , 1 ) − 1 2 ( 1 , 1 , 0 ) = ( 1 2 , − 1 2 , 1 ) \mathbf{b}_2 = \mathbf{a}_2 - \frac{[\mathbf{a}_2,\mathbf{b}_1]}{[\mathbf{b}_1,\mathbf{b}_1]}\mathbf{b}_1 = (1,0,1) - \frac{1}{2}(1,1,0) = (\frac{1}{2},-\frac{1}{2},1)b2=a2−[b1,b1][a2,b1]b1=(1,0,1)−21(1,1,0)=(21,−21,1)
- b 3 = a 3 − [ a 3 , b 1 ] [ b 1 , b 1 ] b 1 − [ a 3 , b 2 ] [ b 2 , b 2 ] b 2 = ( 0 , 1 , 1 ) − 1 2 ( 1 , 1 , 0 ) − 1 / 2 3 / 2 ( 1 2 , − 1 2 , 1 ) = ( − 2 3 , 2 3 , 2 3 ) \mathbf{b}_3 = \mathbf{a}_3 - \frac{[\mathbf{a}_3,\mathbf{b}_1]}{[\mathbf{b}_1,\mathbf{b}_1]}\mathbf{b}_1 - \frac{[\mathbf{a}_3,\mathbf{b}_2]}{[\mathbf{b}_2,\mathbf{b}_2]}\mathbf{b}_2 = (0,1,1) - \frac{1}{2}(1,1,0) - \frac{1/2}{3/2}(\frac{1}{2},-\frac{1}{2},1) = (-\frac{2}{3},\frac{2}{3},\frac{2}{3})b3=a3−[b1,b1][a3,b1]b1−[b2,b2][a3,b2]b2=(0,1,1)−21(1,1,0)−3/21/2(21,−21,1)=(−32,32,32)
最终得到正交向量组:b 1 = ( 1 , 1 , 0 ) \mathbf{b}_1=(1,1,0)b1=(1,1,0),b 2 = ( 1 2 , − 1 2 , 1 ) \mathbf{b}_2=(\frac{1}{2},-\frac{1}{2},1)b2=(21,−21,1),b 3 = ( − 2 3 , 2 3 , 2 3 ) \mathbf{b}_3=(-\frac{2}{3},\frac{2}{3},\frac{2}{3})b3=(−32,32,32)
4、线性方程组
4.1 非齐次
- 线性方程组 A m n A_{mn}Amn * x xx=b 有解的 充要条件 是 r(A,b)= r(A)
- 当线性方程组A m n ∗ x A_{mn} * xAmn∗x=b 有解时:r 为秩,n为系数项数,即未知量的个数(列向量个数)
- 若 r(A,b)= r(A)=r = n,方程组有唯一解
- 若 r(A,b)= r(A)=r < n,方 程组有无穷多解
- 同理, A m n ∗ x A_{mn }* xAmn∗x=b 无解的充要条件是r ( A , b ) ! = r ( A ) r(A,b)!=r(A)r(A,b)!=r(A)
4.2 齐次线性方程组解的判定
齐次线性方程组一定满足:r ( A , b ) r(A,b)r(A,b)=r ( A ) r(A)r(A)
- 齐次线性方程组A m n ∗ x = 0 A_{mn} * x=0Amn∗x=0只有零解的充要条件是 r(A)= n
- 齐次线性方程组A m n ∗ x = 0 A_{mn} * x=0Amn∗x=0有非零解的充要条件是 r(A)< n(有非零解即为无穷多解)
4.3齐次线性方程组的解的结构
解向量的概念
若齐次线性方程组有非零解,则它会有无穷多解,这些解组成一个n维向量组,若能求出该向量组的一个极大无关组,则就能用它来表示它的全部解,这个极大无关组称为齐次线性方程组的基础解系
齐次线性方程组有非零解,则它一定有基础解系。
- 定理1:假设齐次线性方程组A m n ∗ x = 0 A_{mn} * x=0Amn∗x=0的系数矩阵A的秩r ( A ) = r < n r(A)= r < nr(A)=r<n,则A m n ∗ x = 0 A_{mn} * x=0Amn∗x=0的基础解系中有n − r n-rn−r 个解向量
4.4非齐次线性方程组的解的结构
非齐次线性方程组的解的结构为:非齐次线性方程组的特解 + 齐次线性方程组的通解。
求线性方程组通解的一般步骤
齐次线性方程组:
- 对于增广矩阵化简为行最简型矩阵
- 判断解的情况并且得到解向量的个数 = n-r
- 通过行最简矩阵得到自由未知量,首非零元与自由未知量确定方程,求方程解,得到各个未知量的解,并且得到每一个基础解系
- 通解为 各个基础解系的k倍和
非齐次线性方程组:
- 步骤与上面基本一致,但通解为:特解 + 导出组(导出组指的是常数项为0)的基础解系
5. 特征值和特征向量
5.1 基本概念与定理
定义: 设A AA是n nn阶方阵,若存在数λ \lambdaλ和非零向量α \alphaα使得: A α = λ α A\alpha = \lambda\alphaAα=λα, 则称λ \lambdaλ为A AA的特征值,α \alphaα为对应λ \lambdaλ的特征向量。
带参数r的n阶方阵称为A的特征方阵;
它的行列式称为A的特征多项式;
∣ λ E − A ∣ |\lambda E-A|∣λE−A∣=0称为A的特征方程
求解特征值与特征向量的方法:
- n阶实方阵的特征值就是它的特征方程的n个根
- 任意取定一个特征值,其对应特征向量就是相应齐次线性方程组(rE-A)x=0 的所有非零解
例题1:求特征值和特征向量
求矩阵A = [ 3 1 1 3 ] A=\begin{bmatrix}3&1\\1&3\end{bmatrix}A=[3113]的特征值和特征向量。
解:
1. 特征方程:
∣ 3 − λ 1 1 3 − λ ∣ = ( 3 − λ ) 2 − 1 = 0 \begin{vmatrix} 3-\lambda & 1 \\\\ 1 & 3-\lambda \end{vmatrix} = (3-\lambda)^2 -1 = 03−λ113−λ=(3−λ)2−1=0
解得:λ 1 = 2 \lambda_1=2λ1=2,λ 2 = 4 \lambda_2=4λ2=4
2. 求特征向量:
- 对λ 1 = 2 \lambda_1=2λ1=2:
[ 1 1 1 1 ] [ x 1 x 2 ] = 0 ⇒ α 1 = k [ 1 − 1 ] \begin{bmatrix}1&1\\\\1&1\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\end{bmatrix}=0 \Rightarrow \alpha_1=k\begin{bmatrix}1\\\\-1\end{bmatrix}1111x1x2=0⇒α1=k1−1
- 对λ 2 = 4 \lambda_2=4λ2=4:
[ − 1 1 1 − 1 ] [ x 1 x 2 ] = 0 ⇒ α 2 = k [ 1 1 ] \begin{bmatrix}-1&1\\\\1&-1\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\end{bmatrix}=0 \Rightarrow \alpha_2=k\begin{bmatrix}1\\\\1\end{bmatrix}−111−1x1x2=0⇒α2=k11
5.2 矩阵对角化
对角化条件
- A AA有n nn个线性无关特征向量
- A AA的每个特征值的几何重数等于代数重数
例题: 将A = [ 2 − 1 − 1 2 ] A=\begin{bmatrix}2&-1\\\\-1&2\end{bmatrix}A=2−1−12对角化。
解:
- 特征值:λ 1 = 1 \lambda_1=1λ1=1,λ 2 = 3 \lambda_2=3λ2=3
- 特征向量:
- λ 1 = 1 \lambda_1=1λ1=1对应α 1 = ( 1 , 1 ) T \alpha_1=(1,1)^Tα1=(1,1)T
- λ 2 = 3 \lambda_2=3λ2=3对应α 2 = ( − 1 , 1 ) T \alpha_2=(-1,1)^Tα2=(−1,1)T
- 构造矩阵:
P = [ 1 − 1 1 1 ] , P − 1 = 1 2 [ 1 1 − 1 1 ] P=\begin{bmatrix}1&-1\\\\1&1\end{bmatrix}, \quad P^{-1}=\frac{1}{2}\begin{bmatrix}1&1\\\\-1&1\end{bmatrix}P=11−11,P−1=211−111
- 对角化结果:
A = P [ 1 0 0 3 ] P − 1 A=P\begin{bmatrix}1&0\\\\0&3\end{bmatrix}P^{-1}A=P1003P−1
5.3 特征值与特征向量的若干结论
实方阵的特征值未必是实数,特征向量也未必是实向量。
三角矩阵的特征值:
上下三角矩阵的特征值就是它的全体对角元素。特征向量的唯一性:
一个向量 p不可能是同一个方阵A的不同特征值的特征向量。方阵与其转置的特征值关系:
n阶方阵和它的转置具有相同的特征值。特征值与矩阵的关系:
设 r₁, r₂, …, rₙ 为方阵 A的全体特征值,则必有:特征值之和等于对角线元素之和(迹):
∑ i = 1 n λ i = ∑ i = 1 n a i i = tr ( A ) \sum_{i=1}^{n} \lambda_{i} = \sum_{i=1}^{n} a_{ii} = \text{tr}(A)∑i=1nλi=∑i=1naii=tr(A)
特征值之积等于行列式的值:
∏ i = 1 n λ i = ∣ A ∣ \prod_{i=1}^{n} \lambda_{i} = |A|∏i=1nλi=∣A∣
6、二次型
n nn元二次齐次函数:
f ( x 1 , . . . , x n ) = ∑ i = 1 n ∑ j = 1 n a i j x i x j ( a i j = a j i ) f(x_1,...,x_n)=\sum_{i=1}^n\sum_{j=1}^n a_{ij}x_ix_j \quad (a_{ij}=a_{ji})f(x1,...,xn)=i=1∑nj=1∑naijxixj(aij=aji)
矩阵形式:f ( x ) = x T A x f(\mathbf{x})=\mathbf{x}^TA\mathbf{x}f(x)=xTAx
- A(对称矩阵)称为二次型f的矩阵,对称阵A的秩为二次型f的秩
- 二次型与对称阵具有一一对应的关系,一个二次型 f 由其对应的实对称矩阵 A 唯一确定。当给定了二次型 f 后,便许可确定其对应的实对称矩阵 A
- A 的对角线元素为:a i i a_{ii}aii为x i 2 x_{i} ^2xi2项的系数
- A 的其他元素为:a i j = a j i a_{ij} = a_{ji}aij=aji 为 x i j x_{ij}xij 项的系数的 2 − 1 2^{-1}2−1
例题3:化二次型为标准形
化二次型f = 2 x 1 2 + 3 x 2 2 + 4 x 1 x 2 f=2x_1^2+3x_2^2+4x_1x_2f=2x12+3x22+4x1x2为标准形。
解法1(配方法):
f = 2 x 1 2 + 4 x 1 x 2 + 3 x 2 2 = 2 ( x 1 2 + 2 x 1 x 2 + x 2 2 ) + x 2 2 = 2 ( x 1 + x 2 ) 2 + x 2 2 \begin{aligned} f &= 2x_1^2+4x_1x_2+3x_2^2 \\\\ &= 2(x_1^2+2x_1x_2+x_2^2)+x_2^2 \\\\ &= 2(x_1+x_2)^2+x_2^2 \end{aligned}f=2x12+4x1x2+3x22=2(x12+2x1x2+x22)+x22=2(x1+x2)2+x22
令y 1 = x 1 + x 2 y_1=x_1+x_2y1=x1+x2,y 2 = x 2 y_2=x_2y2=x2,则f = 2 y 1 2 + y 2 2 f=2y_1^2+y_2^2f=2y12+y22
解法2(正交变换法):
- 写出矩阵A = [ 2 2 2 3 ] A=\begin{bmatrix}2&2\\\\2&3\end{bmatrix}A=2223
- 求特征值:λ 1 = 1 \lambda_1=1λ1=1,λ 2 = 4 \lambda_2=4λ2=4
- 标准形:f = y 1 2 + 4 y 2 2 f=y_1^2+4y_2^2f=y12+4y22
6.1 标准型
定义:只含平方项的 二次型称为二次型的标准型
正交变换法化二次型为标准型的方法:
- 写出二次型的矩阵A,求其特征值
- 求出特征值对应的特征向量,并且将他们正交单位化
- 将正交单位化后的特征向量依次作为列向量构成正交矩阵 P。
- 做正交变换 x = P y x=Pyx=Py,得二次型的标准型
正交单位化的时候:
- 倘若对应不同的特征值,所以他们正交,直接单位化即可
- 如果对应相同的特征值,所以要首先正交化,然后再单位化
6.2 合同
对于两个矩阵A和B,假如存在可逆矩阵C,使得C T A C = B C^TAC=BCTAC=B,就称A合同(或相合)于B,记作A≃B,也是一种等价关系。因此能够称A和B是合同矩阵。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号