二级制流量算法熵值计算,N-Gram 算法(二:改进) - 教程
2025-09-23 12:41 tlnshuju 阅读(14) 评论(0) 收藏 举报测试例图:
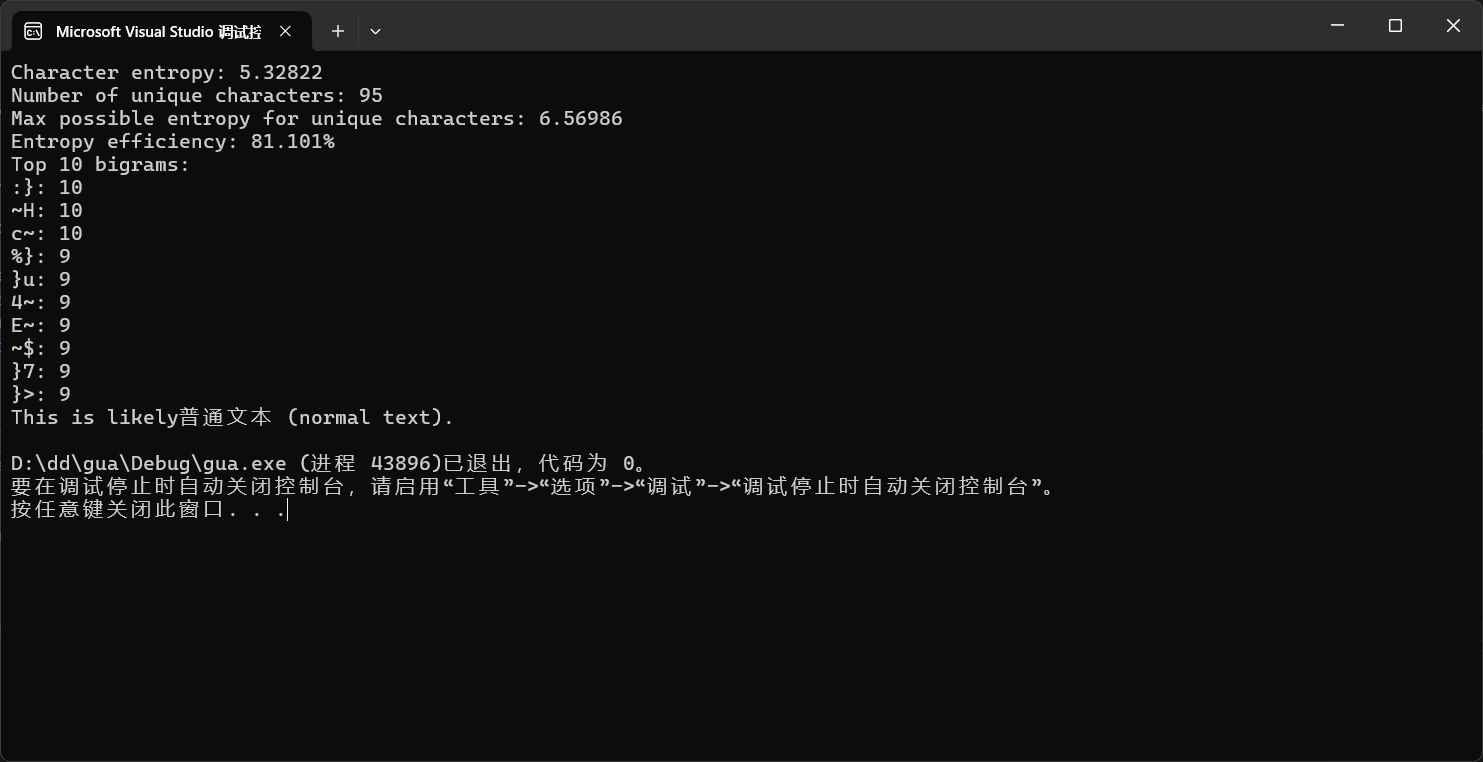
字符熵为5.33,唯一字符数为95,最大可能熵为6.57,熵效率为81.1%。根据之前的分类标准(熵效率>95%为FQ数据)。
完整实现:
#include
#include
#include
#include
#include
#include
using namespace std;
double calculateEntropy(const string& text, int& uniqueChars) {
map freq;
int totalChars = text.length();
if (totalChars == 0) {
uniqueChars = 0;
return 0.0;
}
for (char c : text) {
freq[c]++;
}
uniqueChars = freq.size();
double entropy = 0.0;
for (auto& pair : freq) {
double probability = static_cast(pair.second) / totalChars;
entropy -= probability * log2(probability);
}
return entropy;
}
void printTopBigrams(const string& text, int topN) {
map bigramFreq;
int len = text.length();
for (int i = 0; i > bigrams(bigramFreq.begin(), bigramFreq.end());
sort(bigrams.begin(), bigrams.end(), [](const pair& a, const pair& b) {
return a.second > b.second;
});
cout s}H})~F|}_}02~`~F}E}{}8~+}bL}=@l}d~Si}B}M~@5}u}.H}F}tUT}W~4x})}O~/}8*(B}T~P}u/~^}rp;}YR.%^}P}i~@}K}l~\w}m}.)}u4~Y}hr~\}zWr~:}?wj}7XY~1k3~!}R}F}wq~2&~c~5*V}T}7}cf~?S`~b}+}b};0}:}Zt}d~6~>2}J(~0~`~]=}A~\}C~K"~Mx}{e}S~G~=}>}7i&{>"}7}4~T8~ ~^B}c~:}&K}8~J}/}Q~+}Y%}+i~T~'}(0}&~_}P}M~1}M}Y~&l~4~A[}Z~1}R}{d~!,}K}W~9}Q5F~d~2}f+~[~b~7S}-}>}|}u|@}Q~'f]4f~:~CETGs}p~(~^~K~71~V_$#~,~dQ~=M~/}?}8}u~[t}s_~K}#~O8}.}s}j}c~F~V!z~G]9G}j}>}=8~~8}r'gBJ~I}5}L}4Xq}.~2}&~-}d'~1:}&}d~_~#+~\b~ P}=`l~U}i[~V}Y}~P4}N~^:/~U}G~&mIz~2}J~R|Pt}n}ir~M~H~P$3F~\~KQ=}tdG~(r~.E~%~c~/~0~6%~"~U~%}6}W~E~D};~=[%}E~ ~%~8}3uu}O}j?~dOI~D}"}%}g}C~!}iz}d!~$F~!~$}Z{~4~Ab~:w}h}Eq8dY}*G}k~.}Ho}9}RL}\}]~},9}D~.}j6GO~@2}q6~8}B17}\e~e~V~^R~L~*~9}>}t=}E{}D~0},}[}y}!`d}4}c}0~]k~(}k~=L}-}3}I~K~Hq}5}O:Kg}&~8}V[}B}m}:}y$}i}N}fP0}`p~6~@4~]}|}!}Sx#}"*}pK5}F~Dl~NLb}6}1M~H~/w}WT~5R~P~%}iE~)B~H#~$4~2a8}[+O}]h~E~PX~)~$}h}w}PC~H~@~L}w~C}i}(~&}U ~R}u~`}D}J ~:}*o}A~Q3(}9R}X(~:}3:}/}J~7~D}%}Y}U}=~b|}G}%} }q~H}Q2~N}z},~P~a}(~S?}>}3]}M~R*~Q~W~R}B~-}7.}p(~EwL)";
int uniqueChars;
double entropy = calculateEntropy(data, uniqueChars);
double maxEntropy = log2(uniqueChars);
double entropyEfficiency = entropy / maxEntropy;
cout 0.95) {
cout << "This is likelyFQ数据 (VPN or encrypted data)." << endl;
} else {
cout << "This is likely普通文本 (normal text)." << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号