【数据结构】树的概念 - 详解

01 树的概念

树是一种非线性的数据结构，它是由 n（n >= 0）个有限节点组成的一个具有层次关系的集合。

那么为什么叫 "树" 呢？

我们之所以把它成为 "树"，是因为它很像我们现实生活中的树。只是它是倒过来的，根朝上叶子朝下。

02 树的结构

① 有一个特殊的节点，成为根节点，根节点不存在前驱节点。

② 除根节点外，其余节点被分成 M( M > 0) 个互不相交的集合 T1、T2、……、Tm，其中每一个集合 Ti(1 <= i <= m) 又是一颗结构与树类似的子树。每颗子树的节点有且只有一个前驱，可以有0个或多个后继。

③ 因此，树是递归定义的。因为任何树都会被分成根和子树

注意：树型结构中，子树之间不能有交集，否则就不是树形结构。

03 树的相关概念

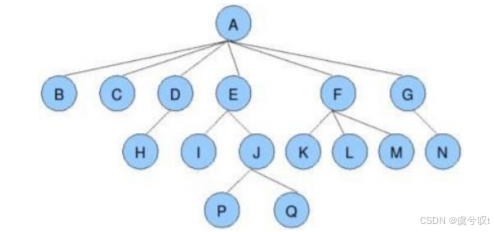
结点的度：一个结点含有的子树的个数称为该结点的度。 比如上图中，A的度为6。

叶子结点：又称终端结点，度为0的结点称为叶子结点。 比如上图中，BCHIPQ等结点就是叶子结点，因为它们的度为0。

分支结点：又称非终端结点，度不为0的结点称为分支结点。 比如上图中，DEFG等结点就是分支结点，因为他们的度不为0。

父结点：又称双亲结点，若一个结点有子结点，则这个结点称作其子结点的父结点。 比如上图中，A是B的父结点。

子结点：又称孩子结点，一个结点含有的子树的根节点称为该结点的子结点。 如上图，B是A的子结点。

兄弟结点：具有相同父结点的结点互相称为兄弟结点。 同一个父亲生的才算。如上图，B和C是兄弟结点，它们的父结点都是A。

树的度：一棵树中最大的结点的度称为树的度。 如上图，最大的结点是A，有6个子树，故A的度为6，所以树的度为6。

结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推。 也有将根定义为第0层，根的子结点为第1层的。但是我们建议还是使用根为第1层来定义比较好。

树的高度：又称树的深度，树中结点的最大层次。 如上图，树的高度为 4。

‍♂️ 堂兄弟结点：父节点在同一层的结点，它们互为堂兄弟。如上图，H 和 I 互为堂兄弟。

结点的祖先：从根到该结点所经分支上的所有结点。 如上图·，A是所有结点的祖先。

‍‍ 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。 如上图，所有结点都是A的子孙。

森林：由 m(m > 0) 棵互不相交的树的集合称为森林。 比如并查集，多个树构成森林。

04 树的表示

下面我们采用三种方式表示下面这课树：

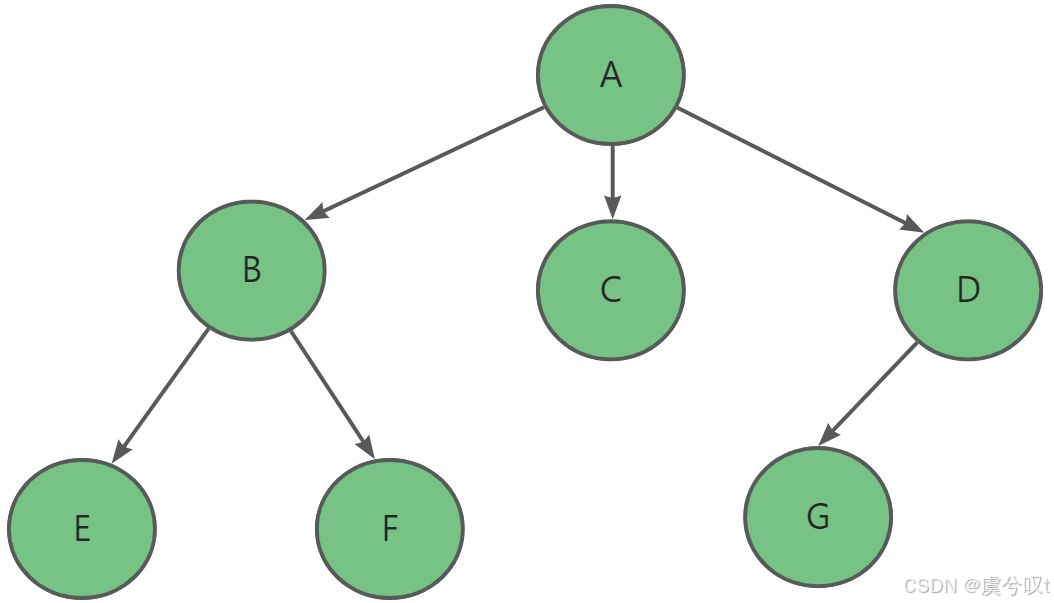
1 双亲表示法

双亲表示法采用顺序表的方式存储，即用顺序表存储各个节点的数据，并且同时存储其双亲节点的下标。注意：根节点没有双亲节点，所以特别记为-1。

#define MAX_SIZE 10
typedef int DataType;
typedef struct Node
{
DataType data;//数据域
int parent; //双亲结点在数组中的位置下标
}Node;
typedef struct PTree
{
//存放树中所有结点
Node tnode[MAX_SIZE];
//当前结点个数
int n;
}PTree;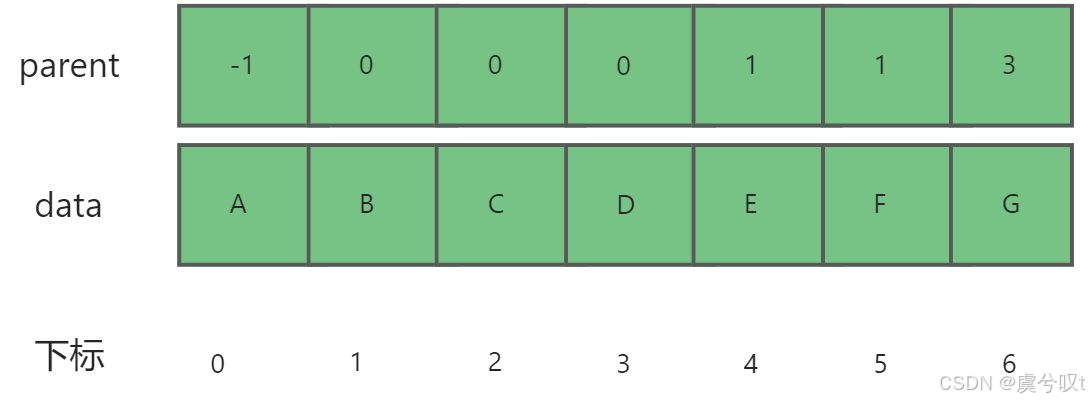

2 树的孩子表示法

树的孩子表示法就是采用顺序表与链表结合的形式，用顺序表存储树的值与链表的头节点，而链表的头节点存储其孩子节点在顺序表中的下标，若没有则记为空。

#define MAX_SIZE 10
#define DataType int
typedef struct ListNode
{
int child;
struct ListNode* next;
}ListNode;
typedef struct TNode
{
DataType data;
//孩子链表的头指针
ListNode* firstchild;
}TNode;
typedef struct PTree{
//存储结点的数组
TNode nodes[MAX_SIZE];
int n; //结点数量
}PTree;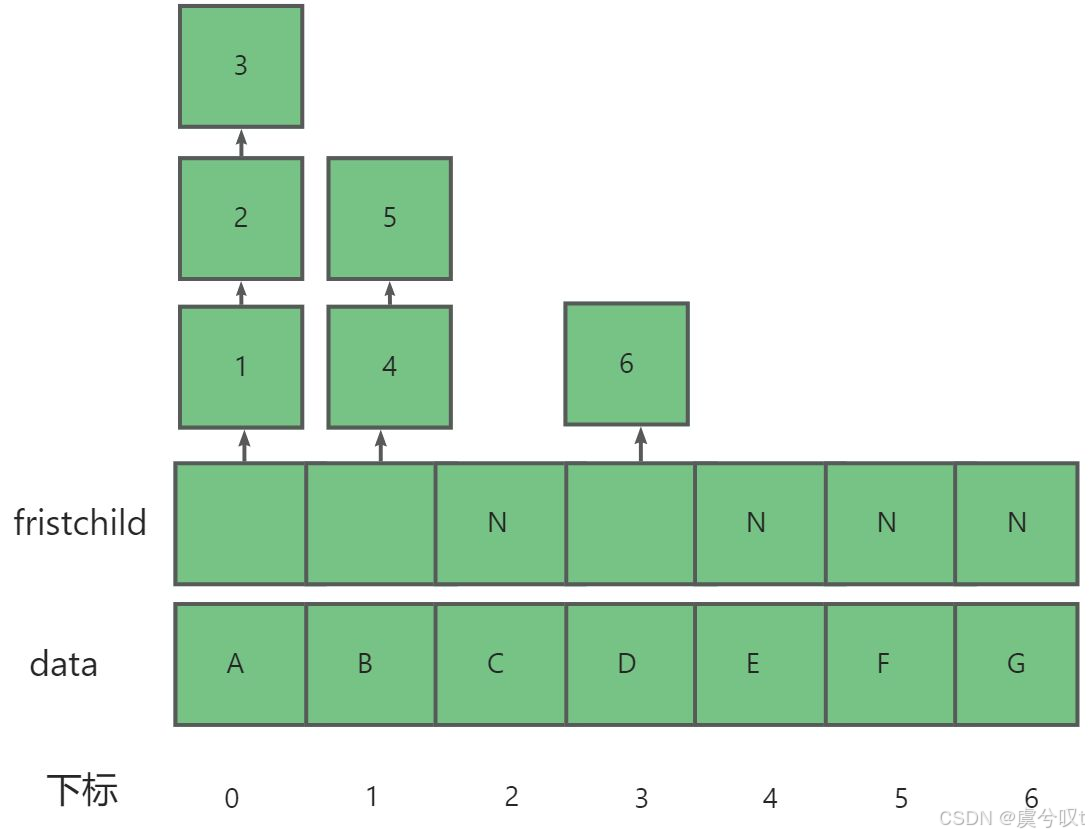

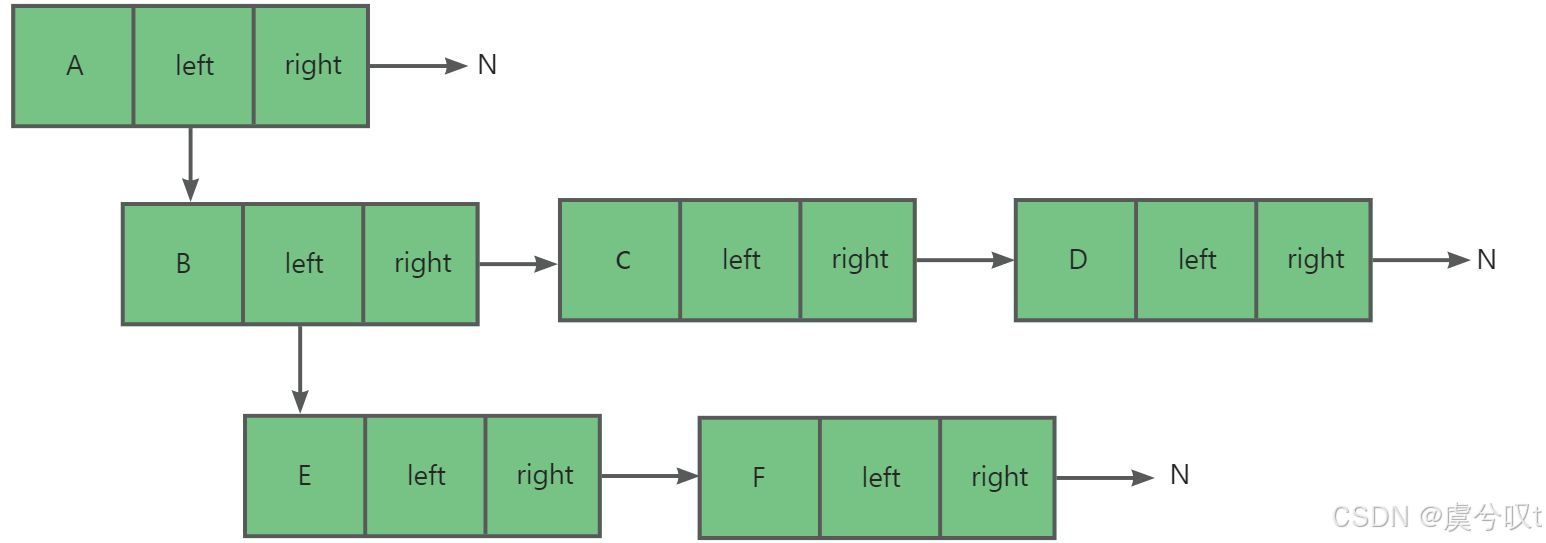
3 左右孩子兄弟表示法

最常用表示树的的方法就是左孩子右兄弟表示法，即定义两个指针，让左指针指向子结点，右指针指向兄弟结点。如果没有结点，则都指向空。

typedef int DataType;
struct Node
{
struct Node* leftChild1; // 孩子结点
struct Node* rightBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};

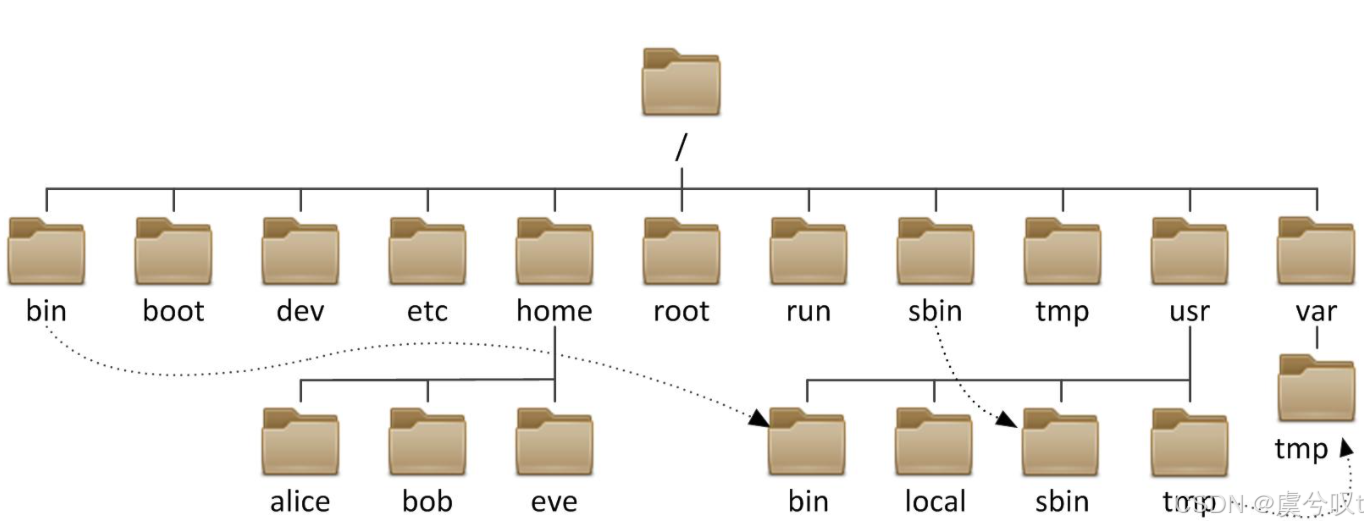
05 树在实际中的应用

文件系统的目录树结构、网络拓扑，最短路径问题，搜索引擎、思维导图等