n个平面分空间最多可分成多少份

最近周围的同学在面试，我保研了，但是也会去参加一些笔试题，其中的智力题目大大令我感兴趣。

这个问题应该可以说是n条直线分平面的推广。熟悉n条直线分平面的问题的话，可知其充要递归条件是：

第n条直线与前面n-1条直线均相交，而且交点不重叠。

如下图所示，第四条直线满足的条件是与前面3条直线相交而且交点不重叠。

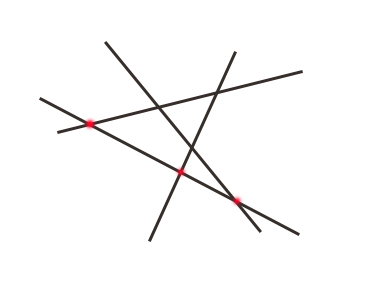
令第n条直线分割的平面数是f(n)，则f(1)=2

我们再来考虑第n条直线，第n条直线与n-1条直线相交，交点不重叠，那么第n条直线被分成了n段。如上面的图可以看出此规律。这n段线段或者射线参与了平面的分割任务，而且他们分别位于n-1条直线分割出来的不同的平面区域内。所以第n条直线加入之后，多出来的平面数量是n。

故有 f(n)=f(n-1)+n.

递归式求出来了，可知f(n)=f(1)+2+3+...+n=1+1+2+3+...+n==

 

 

下面来考虑n个平面分空间的问题。

n个平面分空间的问题的充要递归条件是：

第n个平面必须与前面n-1个平面都相交，而且这n-1个平面产生的交线在第n个平面上满足前面的直线分平面中的条件

如图所示： 黄色平面与前面3个平面的交线在黄色平面上满足上面所述性质。

可以想象，黄色平面被这些交线分割成f(3)个平面区域，这f(3)个平面区域均参与了空间分割任务，把空间一份为2，所以相对于3个平面的情况来说，增加了f(3)个空间区域。

令g(n)为n个平面分空间的空间区域数量，则g(1)=2

第n个平面被n-1条交线分割成f(n-1)个平面区域，而这f(n-1)个平面区域均位于不同的空间区域并参与了空间分割任务，所以增加了f(n-1)个空间区域

故有g(n)=g(n-1)+f(n-1)

可求g(n)=g(n-1)+f(n-1)=g(n-2)+f(n-2)+f(n-1)=...=g(1)+f(1)+...+f(n-1)=2+

对于的通项，百度下可知为，当然也可以自己求，利用等式左右均有3次式进行累加可以消除3次式并求出2次式的通项，

故g(n)=

 

话说上面的递归条件不知道能不能保证存在，估计可以把。