可持久化Trie树(字典树)

举例子：

插入cat：

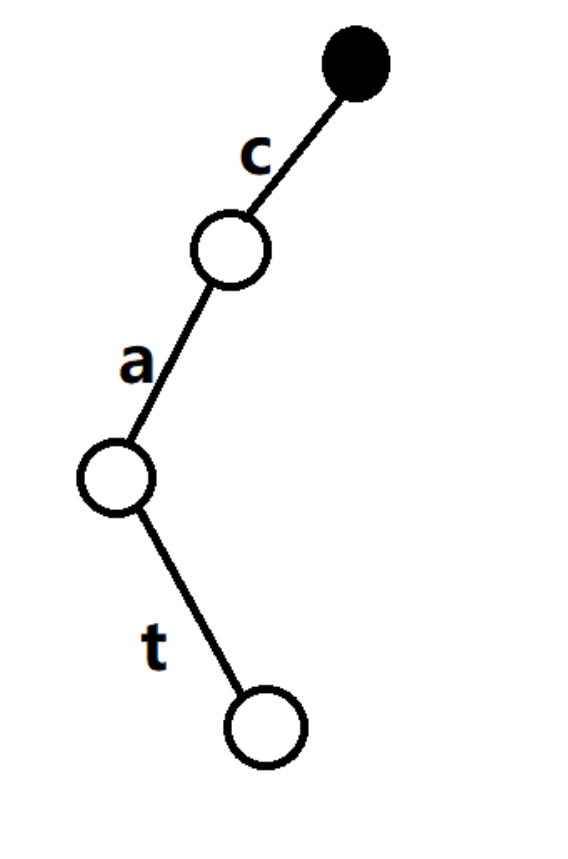
插入cup：

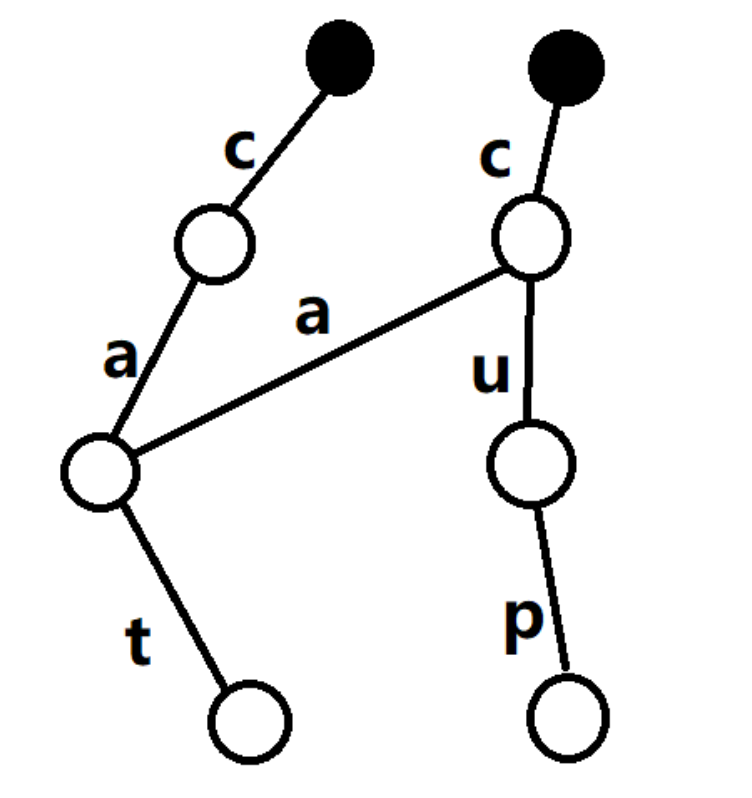
插入soup：

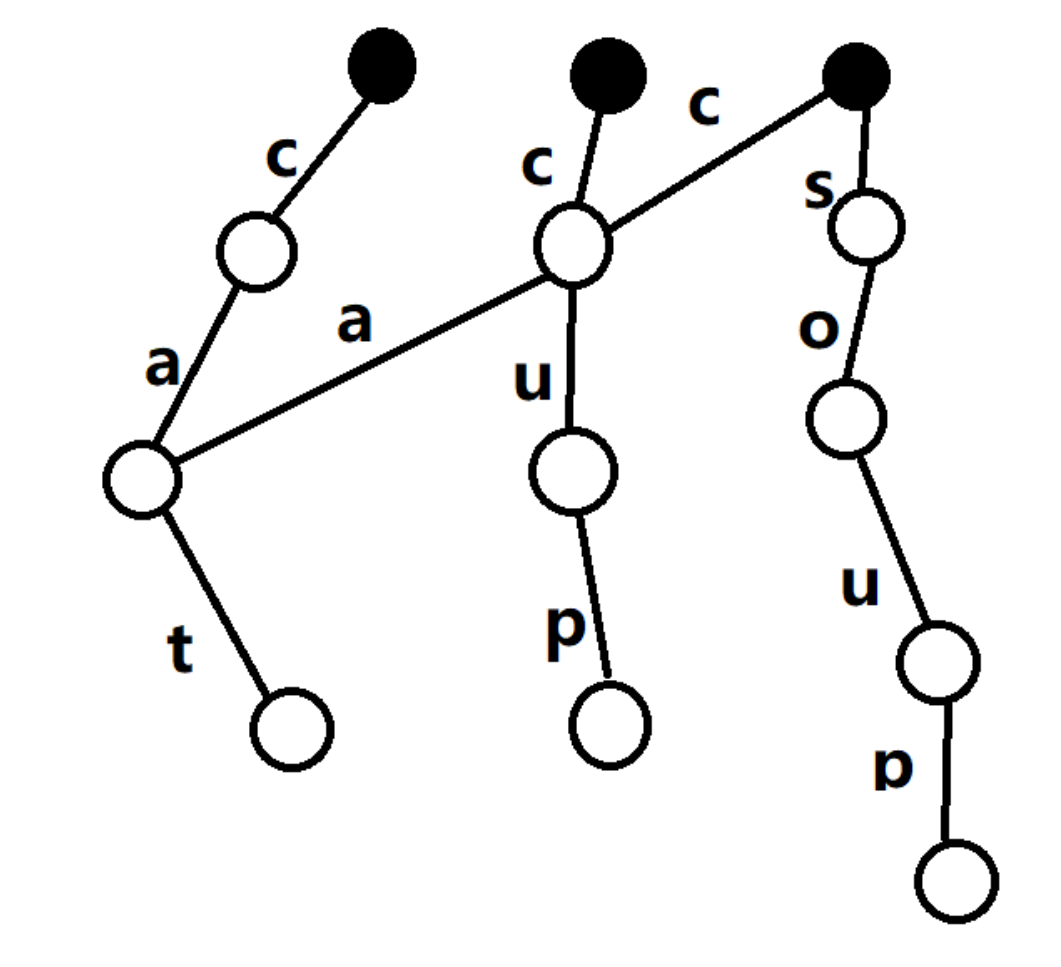
插入cut：

可持久化数据结构的重要问题就是解决区间的查询问题：

例题，洛谷4735：

 

M个操作，

操作1：添加操作，添加一个树x，序列长度+1

操作2：询问操作，找到一个位置p，满足l<=p<=r，使得a[p] ^ a[p+1] ^ ... ^ a[N] ^ x 最大，输出最大值

 

分析：

令S[k] = a[1] xor a[2] xor ... xor a[k]

  a[p] xor a[p+1] xor ... xor a[N] xor x

=(a[1] xor a[2] xor ... xor a[p-1])  xor (a[1] xor a[2] xor ... xor a[N]) xor x

=s[p-1] xor s[N] xor x

(p = 1时，a[1] xor a[2] xor ... xor a[N] xor x = s[0] xor s[N] xor x，所以s[0] = 0)

又因为s[N] xor x是定值，设为v

此时查询转变为：求一个p∈[l-1,r-1] 使得 s[p] ^ x 最大

 

思路：

构建一个可持久化0/1Trie树，第i个版本为插入了s[i]后的Trie树，初始版本0就是插入s[0]=0的tree树

每次查询，从根节点开始，贪心地选与这一位相反的值

先考虑查询[1,r]的区间，即查询[0,r-1]的区间，只需要拿出版本为r-1的Trie树，按照上面的贪心方法，即可得到[0,r-1]区间内与定值v的异或最大值

再考虑查询[l,r]的区间，即查询[l-1,r-1]的区间，依然可以拿出版本为r-1的Trie树，查询的时候尽量向着相反的方向跳，但不能超过左侧边界l-1，对每个节点维护一个ver，

ver[i]表示第一次被创建的版本。这样，在查询时只访问ver>=l−1的节点就行了。

 ver[0]代表所有的不能走的空结点，因为不能走，所以要比最小的l-1(0)要小，这样就会在判断l-1时条件时候避免走空结点，设为-1

 

 

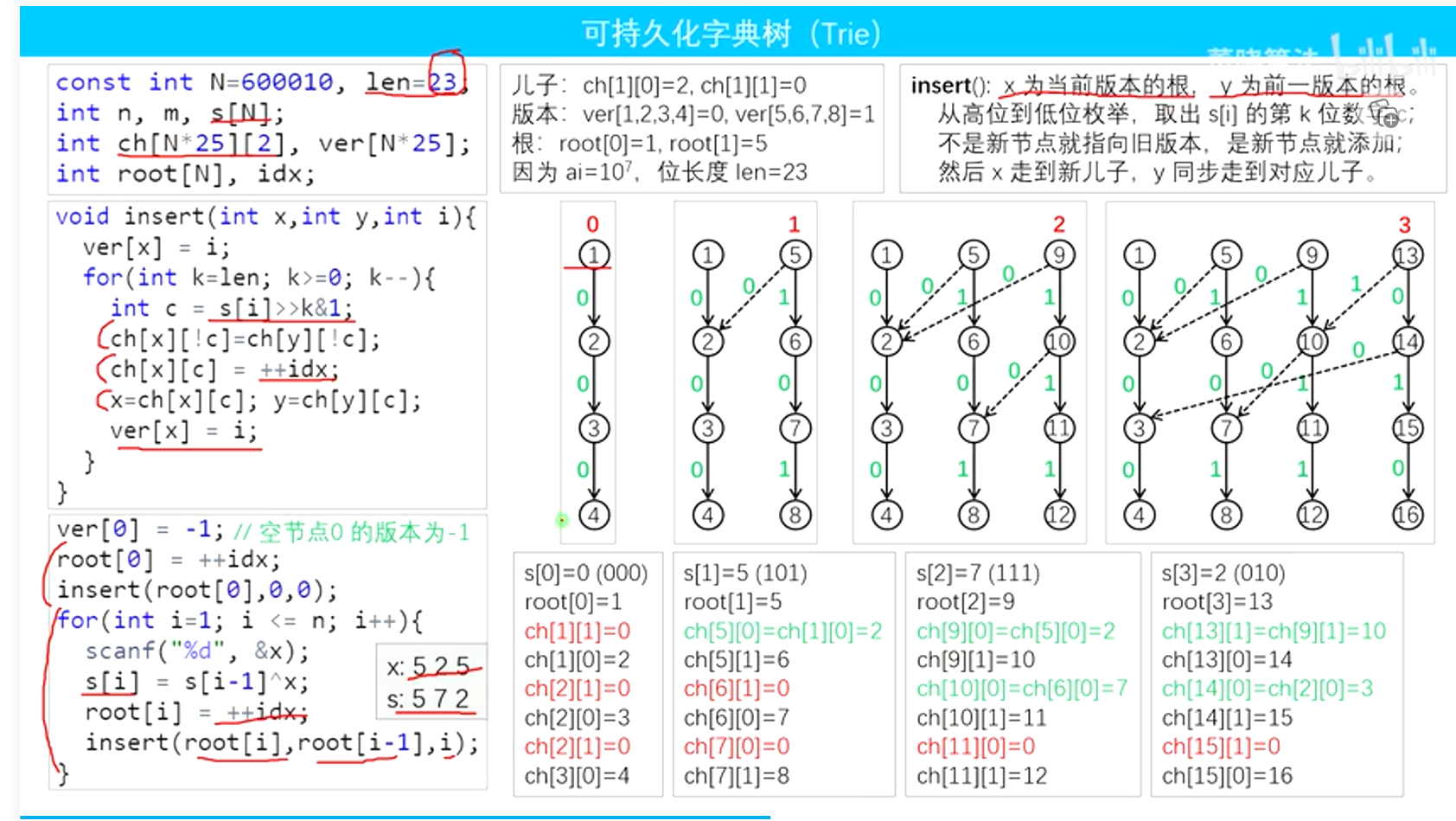
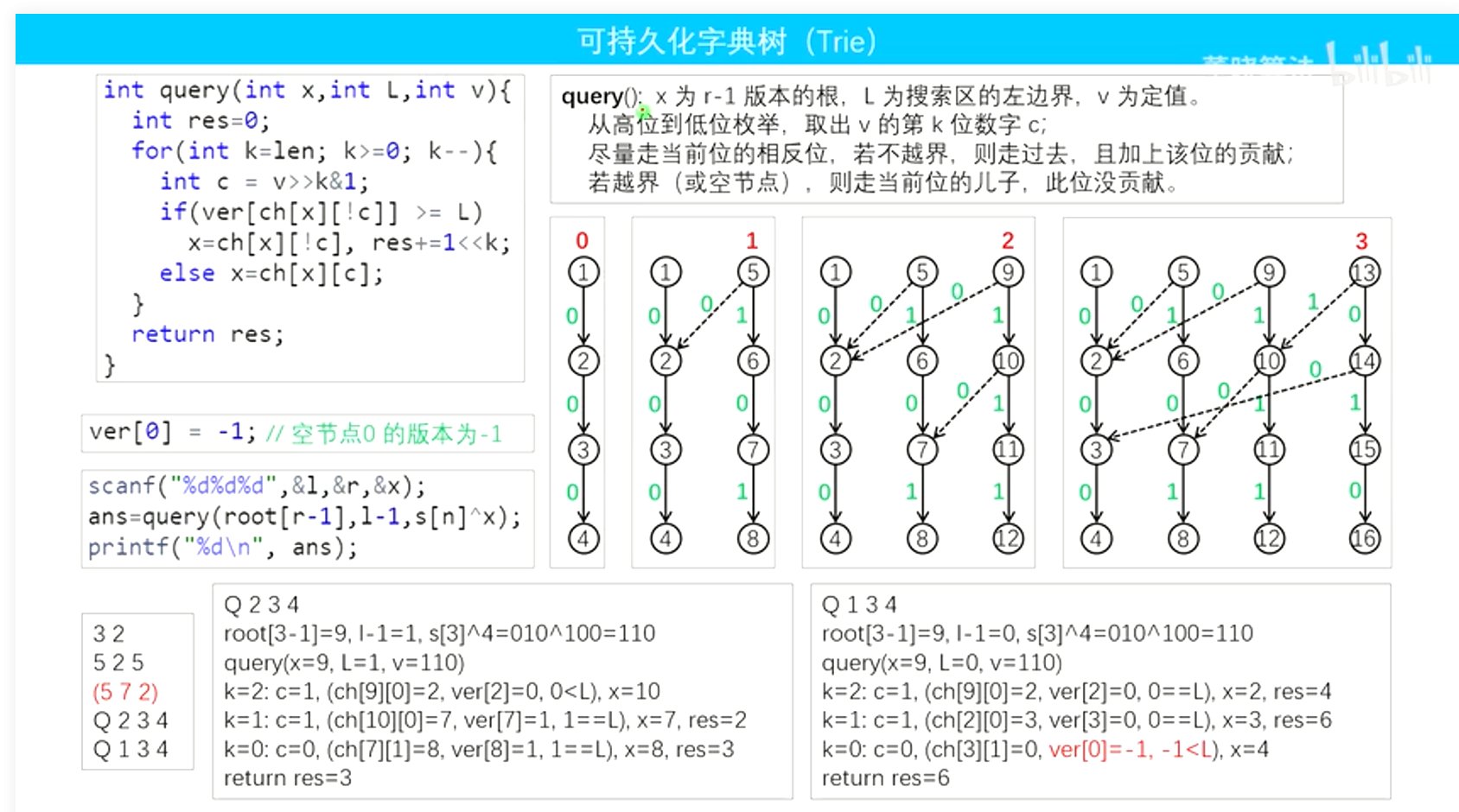
 代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 6e5 + 10;

int s[N]; // s[i]代表a[1]^a[2]^...^a[i],s[0]=0
int n, m;
int len = 23;          // 0<=a[i]<=1e7,最多23位,所以最多23*N个结点
int ver[25 * N], idx; // ver代表每个结点所属版本,idx代表树中每个结点的编号
int son[25 * N][2];      //每个结点的孩子的编号
int root[N];          // s[0~N]->每插入一个算一个版本,有版本0~N,root代表每个版本的根

// 三个参数代表,当前版本的根now,前一个版本的根pre,当前版本号i
void insert(int now, int pre, int i)
{
    ver[now] = i;
    for (int k = len; k >= 0; k--)
    {
        int u = s[i] >> k & 1;
        son[now][!u] = son[pre][!u];
        son[now][u] = ++idx;
        now = son[now][u], pre = son[pre][u];
        ver[now] = i;
    }
}
//在版本[l-1,r-1]中查找最大值，三个参数分别为root[r-1],l-1,定值s[n]^x
int query(int R, int L, int v)
{
    int res = 0;
    for (int k = len; k >= 0; k--)
    {
        int u = v >> k & 1;
        //如果可以走反方向
        if (ver[son[R][!u]] >= L)
        {
            res |= 1 << k;
            R = son[R][!u];
        }
        else
            R = son[R][u];
    }
    return res;
}
int main()
{
    cin >> n >> m;
    ver[0] = -1; //结点编号为0代表空结点
    root[0] = ++idx;
    //插入s[0]产生版本0
    insert(root[0], 0, 0);
    for (int i = 1; i <= n; i++)
    {
        cin >> s[i];
        s[i] ^= s[i - 1];
        root[i] = ++idx;
        //每插入一个s[i]产生一个版本
        insert(root[i], root[i - 1], i);
    }
    // m次询问
    for (int i = 1; i <= m; i++)
    {
        char op;
        cin >> op;
        if (op == 'A')
        {
            n++;
            cin >> s[n];
            s[n] ^= s[n - 1];
            root[n] = ++idx;
            insert(root[n], root[n - 1], n);
        }
        else
        {
            int l, r, x;
            cin >> l >> r >> x;
            cout << query(root[r - 1], l - 1, x ^ s[n]) << endl;
        }
    }
    return 0;
}