Solution of CF911G Mass Change Queries

Summary of the question:

You are given an array \(a\) consisting of \(n\) integers. You have to process \(q\) queries to this array; each query is given as four numbers \(l,r,x\) and \(y\), denoting that for every \(i\) such that \(l<=i<=r\) and \(a_i=x\) you have to set \(a_i\) equal to \(y\).

Print the array after all queries are processed

Input

The first line contains one integer \(n(1<=n<=200000)\)-the size of array \(a\).

The second line contains \(n\) integers \(a_1,a_2,...,a_n(1<=a_i<=100)\) - the elements of array \(a\).

The third line contains one integer \(q(1<=q<=200000)\) - the number of queries you have to process.

Then \(q\) lines follow. \(i\) -th line contains four integers \(l,r,x\) and \(y\) denoting \(i\) -th query \((1<=l<=r<=n,1<=x,y<=100)\)

Output

print \(n\) integers - elements of array \(a\) after all changes are made

Solution

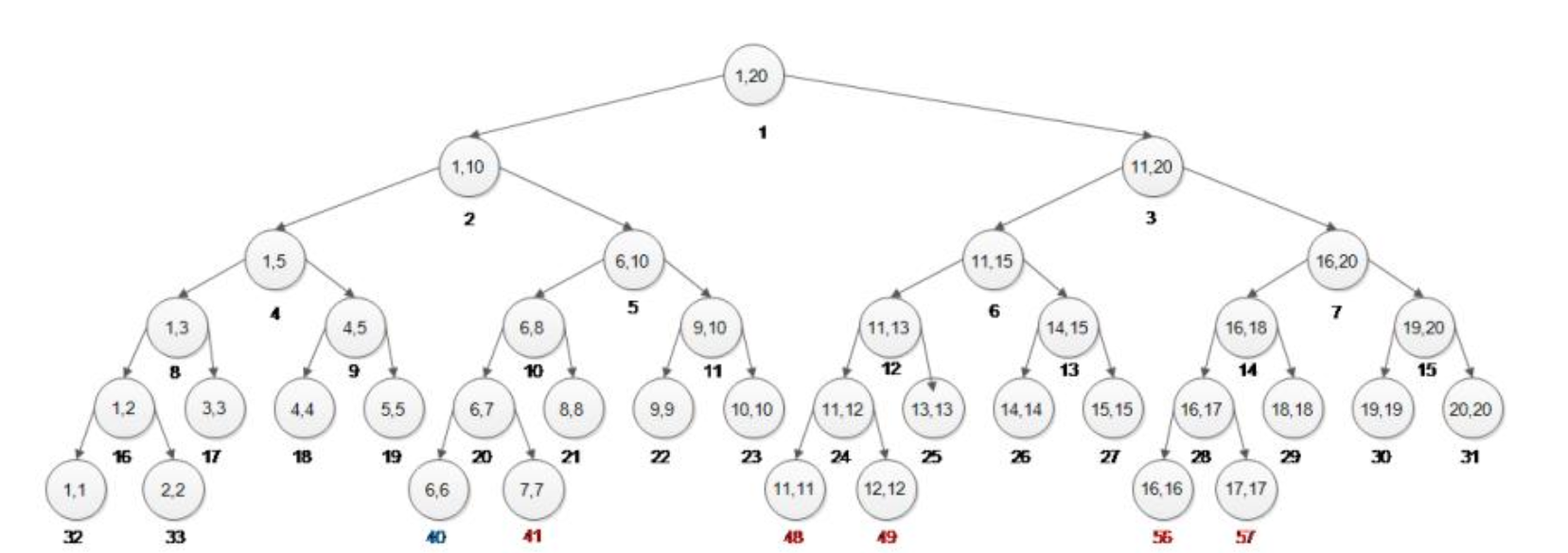
It is obvious we could use segment tree to solve this question, but the problem is that what do we do with the 100 kinds of elements.

The good thing is that there were only 100 kinds of elements, so we were able to record all the information about the operation on the nodes of the segment tree. All we have to do is open a hundred space to record the number.

When we need to modify the number, it will be ok for us to do a for loop to ergodic all the points on that knot.

Although it can AC the question, but it took you about 1s to pass the final data.

There were some different solution that I didn't use in my coding. We could use the technique of blocking. Also we could use Dynamic open point segment tree.

Calculation about time and space

space:\(O(200000*100*4)\)

time:\(O(n*log n*100)\)

Here's my coding

#include<bits/stdc++.h>
#define N 200005
using namespace std;
struct node{
	int sum[101];
}tree[N*4];
int a[N],n,m,x,y,l,r;
inline void pushdown(int p){
	for (int i=1;i<101;i++){
		tree[p<<1].sum[i]=tree[p].sum[tree[p<<1].sum[i]];
		tree[p<<1|1].sum[i]=tree[p].sum[tree[p<<1|1].sum[i]];
	}
	for (int i=1;i<101;i++)
		tree[p].sum[i]=i;
}
void build(int p,int l,int r){
	for (int i=1;i<101;i++)
		tree[p].sum[i]=i;
	if (l==r) return;
	int mid=(l+r) >> 1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r); 
}
void modify(int p,int l,int r,int x,int y,int from,int to){
	if (l>=x&&r<=y){
		for (int i=1;i<101;i++)
			if (tree[p].sum[i]==from)
				tree[p].sum[i]=to;
		return;
	}
	int mid=(l+r) >> 1;
	pushdown(p);
	if (x<=mid) modify(p<<1,l,mid,x,y,from,to);
	if (y>mid) modify(p<<1|1,mid+1,r,x,y,from,to); 
}
void query(int p,int l,int r){
	if (l==r){
		printf("%d ",tree[p].sum[a[l]]);
		return;
	}
	pushdown(p);
	int mid=(l+r)>> 1;
	query(p<<1,l,mid);
	query(p<<1|1,mid+1,r);
}
int main(){
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	build(1,1,n);
	scanf("%d",&m);
	for (int i=1;i<=m;i++){
		scanf("%d%d%d%d",&l,&r,&x,&y);
		modify(1,1,n,l,r,x,y);
	} 
	query(1,1,n);
	return 0;
}