北航OO第一单元总结
1.度量分析
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Maps.print() | 29.0 | 5.0 | 15.0 | 16.0 |
| Maps.filter() | 1.0 | 1.0 | 2.0 | 2.0 |
| Maps.add(Item) | 2.0 | 1.0 | 2.0 | 2.0 |
| Main.main(String[]) | 16.0 | 1.0 | 9.0 | 9.0 |
| Item.update(String) | 5.0 | 1.0 | 3.0 | 3.0 |
| Item.opposite() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getIndex() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 53.0 | 12.0 | 34.0 | 35.0 |
| Average | 6.625 | 1.5 | 4.25 | 4.375 |
可以看出复杂度最高的为print()方法,这是因为本次作业中我构建Maps保存读入的字符串,将求导以及输出的部分融合在了print()方法中,这也导致了后续的重构。
2. UML类图
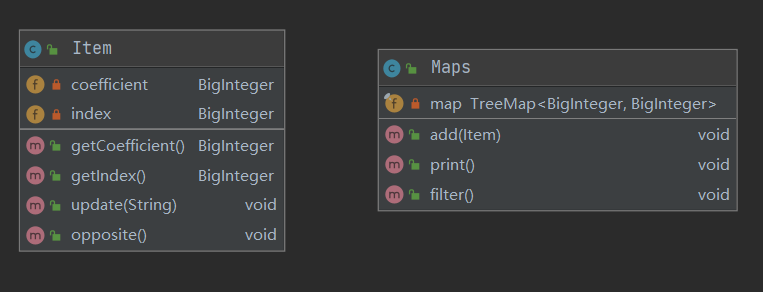
Item用来保存一个由系数和指数组成的项,Maps由若干个项组成。
3.作业总结
由于第一次作业中形式较为简单,只需要考虑简单幂函数的求导,并且去掉空格没有任何成本,在不考虑违法输入的情况下我选择了构建表达式树,将整个表达式拆解为由系数和指数组成的项,并将每个项保存在Treemap中,最后对每个项 实现求导操作再将结果输出即通过了测试。
在本次作业中,具体实现的思路其实仍然属于面向过程的思维,一步一步将一个字符串读入进来构建成一个表达式,由于问题并不复杂,实现的过程也十分顺利,但是在构建思路的过程中并没有仔细去想可扩展性的问题,这也导致了后续作业的重构。
二、第二次作业
1.度量分析
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Term.toString() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.toPrint() | 32.0 | 1.0 | 16.0 | 16.0 |
| Term.Term(String) | 14.0 | 2.0 | 8.0 | 8.0 |
| Term.opposite() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.mul(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.getKey() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.derivation() | 4.0 | 2.0 | 4.0 | 5.0 |
| Term.add(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| Main.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.print() | 5.0 | 1.0 | 5.0 | 5.0 |
| Expression.opposite() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.mulTerm(Term) | 4.0 | 1.0 | 3.0 | 3.0 |
| Expression.mulexpression(Expression) | 7.0 | 1.0 | 4.0 | 4.0 |
| Expression.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.getindex(String) | 6.0 | 3.0 | 3.0 | 5.0 |
| Expression.filter() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.Expression(String) | 22.0 | 2.0 | 10.0 | 11.0 |
| Expression.derivation() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.addTerm(Term) | 2.0 | 1.0 | 2.0 | 2.0 |
| Expression.addexpression(Expression) | 1.0 | 1.0 | 2.0 | 2.0 |
| Total | 110.0 | 43.0 | 89.0 | 97.0 |
| Average | 3.6666666666666665 | 1.4333333333333333 | 2.966666666666667 | 3.2333333333333334 |
本次作业中类的数目很少,复杂度主要集中在了表达式的构建与Term的输出,表达式的构建应该是本次作业中最为重要的一部分,而项的输出部分过多的分类讨论导致该方法复杂度大大增加,这样的输出方式不是一个良好的工程化方法,应该在以后的作业中养成更好的习惯。
2.UML类图
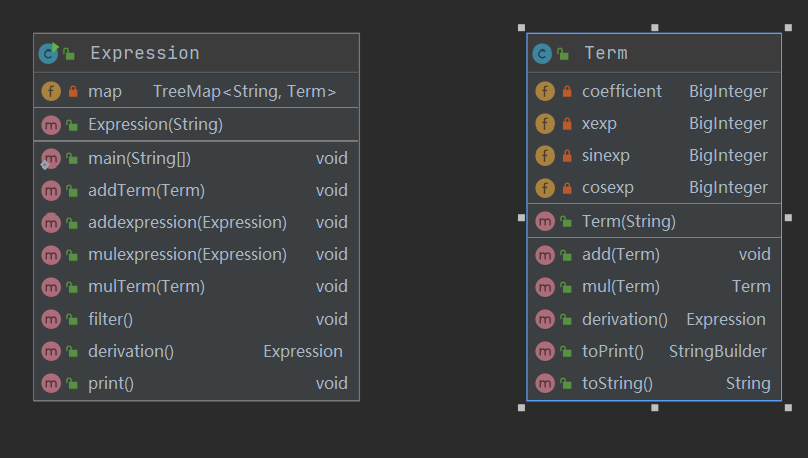
与第一次作业不同的地方在于Term增加了两个参数,分别表示sin(x)与cos(x)的指数,在构建表达式的过程中使用了递归下降的思路,其余部分与第一次作业类似。
3.作业总结
第二次作业中增加了sin(x)和cos(x),但是在我实现过程中存储的方式与第一次作业没有什么本质不同,最开始也是同样选择了无成本的去掉所有空格,到第二次作业我仍然没有选择构建factor因子,而是将每个term项扩展,增加了sin指数与cos指数,构建表达式的过程依然是从字符串一点一点读入,本次作业的难点在于增加了表达式因子的嵌套,虽然在此之前我没有了解过递归下降这一方法,不过由于我整个实现的过程是将每个项用四个参数存储在treemap中,于是想到了每当读到一个左括号时去寻找与之匹配的右括号,将括号里面的内容利用表达式的构造函数构造出新的表达式,再将得到的表达式与原表达式相乘,这样便实现了表达式的构造,求导的过程依然是通过实现每个项的求导来完成的,实现的过程也比较顺畅,没有遇到难找的bug。
第二次作业中我依然保存着大量面向过程的思维,但是在实现表达式与项的加减乘除等方法后,我尝到了一丝面向对象的甜头,只通过四个参数来保存一个项的简介让我在第二次作业中完成的十分顺畅,但是这也为我第三次作业遇到的困难埋下了伏笔。
三、第三次作业
1.度量分析
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Cosexp.clonee() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cosexp.Cosexp(BigInteger,Expression) | 0.0 | 1.0 | 1.0 | 1.0 |
| Cosexp.derivation() | 4.0 | 2.0 | 3.0 | 5.0 |
| Cosexp.fileter() | 1.0 | 1.0 | 2.0 | 2.0 |
| Cosexp.tofind() | 0.0 | 1.0 | 1.0 | 1.0 |
| Cosexp.toString() | 5.0 | 5.0 | 5.0 | 5.0 |
| Expression.addexpression(Expression) | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.addTerm(Term) | 2.0 | 1.0 | 2.0 | 2.0 |
| Expression.clonee() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.derivation() | 4.0 | 1.0 | 4.0 | 5.0 |
| Expression.eat(StringBuilder) | 9.0 | 3.0 | 6.0 | 8.0 |
| Expression.eatblank(StringBuilder) | 2.0 | 2.0 | 2.0 | 3.0 |
| Expression.Expression(StringBuilder) | 18.0 | 8.0 | 10.0 | 14.0 |
| Expression.filter() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.getcos(String) | 14.0 | 6.0 | 4.0 | 7.0 |
| Expression.getindex(String) | 6.0 | 3.0 | 3.0 | 5.0 |
| Expression.getMap() | 0.0 | 1.0 | 1.0 | 1.0 |
| Expression.getnums() | 7.0 | 5.0 | 3.0 | 6.0 |
| Expression.getsin(String) | 14.0 | 6.0 | 4.0 | 7.0 |
| Expression.judge(String) | 10.0 | 6.0 | 5.0 | 10.0 |
| Expression.mulconst(BigInteger) | 2.0 | 2.0 | 3.0 | 3.0 |
| Expression.mulexpression(Expression) | 8.0 | 1.0 | 5.0 | 5.0 |
| Expression.mulfactor(Factor) | 5.0 | 2.0 | 4.0 | 4.0 |
| Expression.mulTerm(Term) | 4.0 | 1.0 | 3.0 | 3.0 |
| Expression.opposite() | 1.0 | 1.0 | 2.0 | 2.0 |
| Expression.toString() | 5.0 | 1.0 | 5.0 | 5.0 |
| Expression.update(StringBuilder) | 17.0 | 9.0 | 9.0 | 10.0 |
| Factor.clonee() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.derivation() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.Factor(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.fileter() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.getExp() | 0.0 | 1.0 | 1.0 | 1.0 |
| Factor.setExp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| FormatExc.print() | 0.0 | 1.0 | 1.0 | 1.0 |
| Main.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| Sinexp.clonee() | 0.0 | 1.0 | 1.0 | 1.0 |
| Sinexp.derivation() | 4.0 | 2.0 | 3.0 | 5.0 |
| Sinexp.fileter() | 1.0 | 1.0 | 2.0 | 2.0 |
| Sinexp.Sinexp(BigInteger,Expression) | 0.0 | 1.0 | 1.0 | 1.0 |
| Sinexp.tofind() | 0.0 | 1.0 | 1.0 | 1.0 |
| Sinexp.toString() | 5.0 | 5.0 | 5.0 | 5.0 |
| Term.add(Term) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.clonee() | 1.0 | 1.0 | 2.0 | 2.0 |
| Term.derivation() | 10.0 | 2.0 | 6.0 | 8.0 |
| Term.filter() | 1.0 | 1.0 | 2.0 | 2.0 |
| Term.getCoefficient() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.getTermmap() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.mul(Term) | 1.0 | 1.0 | 2.0 | 2.0 |
| Term.mulconst(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.mulfactor(Factor) | 3.0 | 3.0 | 3.0 | 3.0 |
| Term.opposite() | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.putfactor(Factor) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.setCoefficient(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Term.tofind() | 3.0 | 1.0 | 3.0 | 3.0 |
| Term.toString() | 5.0 | 1.0 | 6.0 | 6.0 |
| Xexp.clonee() | 0.0 | 1.0 | 1.0 | 1.0 |
| Xexp.derivation() | 4.0 | 2.0 | 3.0 | 5.0 |
| Xexp.fileter() | 0.0 | 1.0 | 1.0 | 1.0 |
| Xexp.tofind() | 0.0 | 1.0 | 1.0 | 1.0 |
| Xexp.toString() | 2.0 | 3.0 | 2.0 | 3.0 |
| Xexp.Xexp(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 193.0 | 135.0 | 175.0 | 213.0 |
| Average | 2.757142857142857 | 1.9285714285714286 | 2.5 | 3.0428571428571427 |
与前两次作业相比一个进步的地方在于我没有去刻意实现print()方法,而是将其转换为toString()方法,这样避免了一个复杂度很高的方法的构建,没有使整个作业分离成互不相干的若干部分,也更符合面向对象的思维方式,在将来我也应该培养这样良好的面向对象思维。
2.UML类图
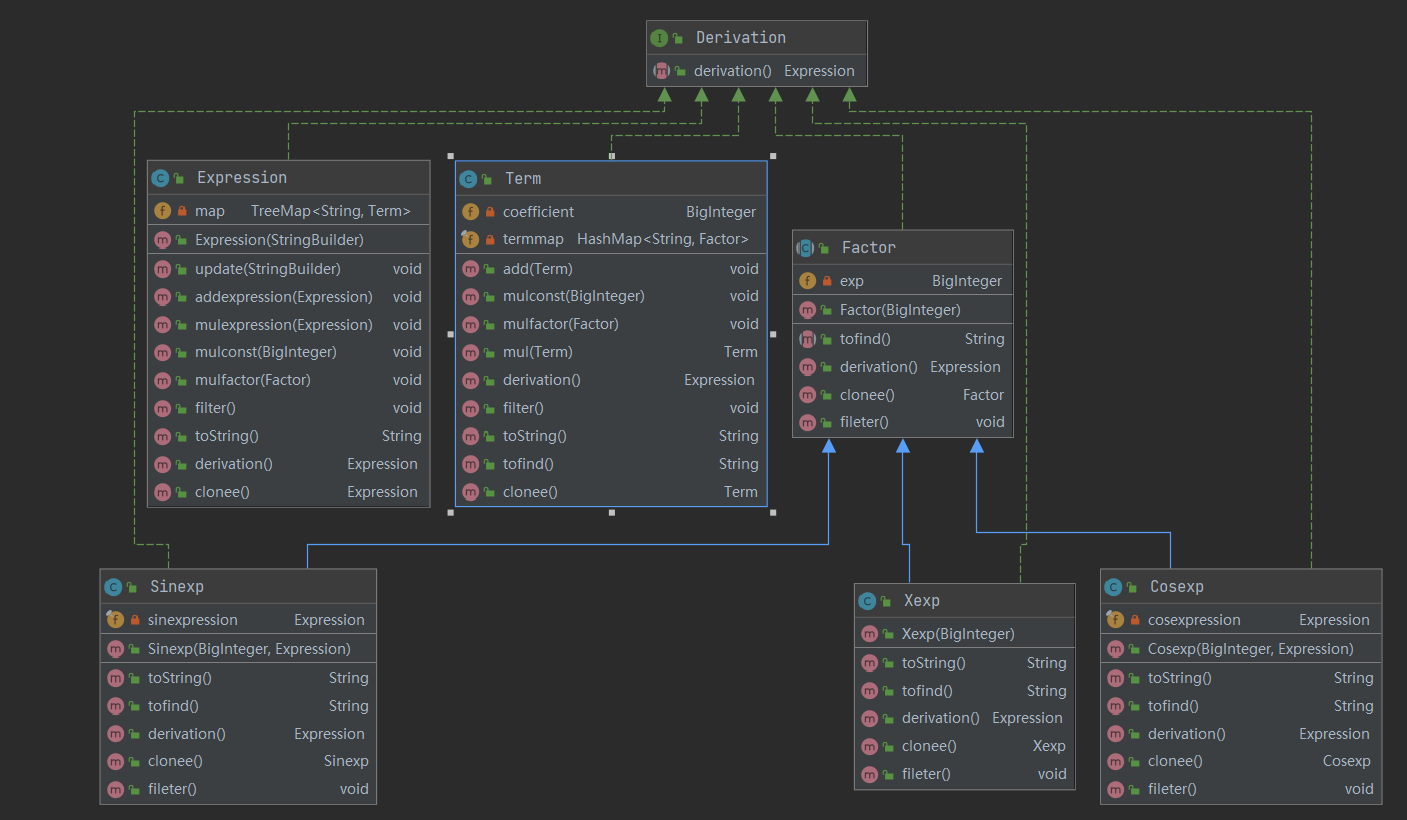
Factor表示将指数作为参数的因子,Sinexp、Cosexp、Xexp都继承了这个类并增加了自己特有的参数,三个类都实现了求导克隆等方法,Term表示由若干因子组成的项,使用HashMao保存这些因子,Expression使用TreeMap保存不同的项,他们都实现了加法和乘法以及求导克隆等操作。
3.作业总结
听到很多同学说第一次作业到第二次作业的过渡比较困难,但第二次到第三次则十分顺畅,不过对我来说确实恰恰相反。前两次作业为了贪图省事,我直接去掉了读入字符串中的所有空白字符,并且题目中合法输入的保证让我在实现过程中可以肆无忌惮的将所有可能出现的情况罗列出来一一解决,但第三次作业中格式审查的出现则是给了我当头一棒。
格式审查是我遇到的第一个难点,由于前两次作业贪图省事去掉空白字符,刚拿到第三次作业后为了延续前面的思路我打算将格式检查与读字符串构建表达式分开进行,但是具体进行格式检查时我却发现想要独立完成这一工作十分艰难,难度系数并不亚于构建表达式的过程。这个时候我想到可以在构建表达式的同时进行格式检查,并且沿用原来的思维,读到一个部分后便罗列出此时所有可能出现的情况,将所有情况一一解决,若不属于这些情况则直接输出WRONG FORMAT!即可,这一想法的出现也让我看到了光明。
但是不久我便遇到了第二个困难,在第二次作业中我使用一个系数三个指数来存储一个项,但是第三次作业中sin与cos都可以包含因子的嵌套,这让我如果将一个项以量化的方式存储下来呢?sin与cos的多样性让被逼无奈的我构建了factor因子,将sin、cos与x的整数幂作为一个子类继承Factor,但是难点在于如何将若干factor保存在一个term中。经过一番思考后我想到,现在不能使用原来的思路将指数直接作为参数来区分不同的因子,但是我最终要实现的就是把表达式以字符串的形式输入,那么我在构造的过程中可以预先借用一下这个方法,将其作为treemap中的键来构建我自己的表达式。至此,这一个问题也得到了解决。事实上,实现的过程中我发现直接将想要输出的结果作为键是不合适的,为了方便的实现加减乘过程中的合并同类项,我需要将我每个因子的指数以及每个项的系数隐藏起来,这推动我实现了一个与最终输出toString类似的tofind方法,将其作为键把每个因子每个项存储下来。
这样,我实现过程中遇到的困难全部解决了,但是在我顺利的完成代码编写后却发现我无法通过测试,此时的我发现了一个隐藏在水下的巨大bug,就是我从来没有实现因子或项的clone方法,这也导致了我调试过程中发现两个表达式相乘,一个已经保存好的项突然发生变化的“灵异事件”,在我实现了clone方法后这一问题终于得到了解决。不过由于需要用到clone方法的地方太多,我修改的过程中没有改全,导致强测时挂了两个点,这也让我感受到了管理一个大项目的艰难。到了第三次作业,我有了更多面向对象的思维方式,希望能在后续作业的完成中更加顺利,取得更多进步。
三次作业总结
1.寻找别人Bug
实际上在寻找别人bug方面我算是比较佛系的,由于前两次作业难度比较简单,特殊情况较少,我手动构造了几个简单的测试数据,在第二次作业时尝试搭建了一个简单的自动评测机,但是并没有发挥作用。第三次作业在完成作业的过程中我将发现的每一个坑点记录了下来,并且作为互测数据尝试了提交。
寻找别人bug的过程中我没有去尝试阅读别人的代码,因为我觉得我很难通过阅读源代码找到一个人的bug,而且读懂别人的代码也是一件比较困难的事,我觉得在之后的作业中我可以更多的把重心放在尝试搭建自动评测机上,自动评测机不仅是评测的一部分,他对作业思路的构建也会提供很大的帮助。
2.重构经历
三次作业中其实整体实现的思路没有太大变化,但是具体代码的编写发生了很大的变化,第二次作业中我的类数目还停留在3,每次作业的偷懒导致我没有保证良好的可扩展性,这也导致我虽然三次作业思路基本相同,但最后代码的实现部分却几乎全部都是推翻重写,以后的作业我也应该更多的去考虑可扩展性的需求,为后面的增量开发提供更大的便利。
3.心得体会
经过了一个单元的学习,我感觉在面向对象的方向正渐渐走入正轨,也取得了很多的收获。
-
前两次作业都没有很好的考虑可扩展性的需求,(第三次作业反而发现如果还有第四次作业可扩展性应该还不错?),后面几个单元的学习过程应该更多去思考作业可能还会在哪些方面有扩展的需求,如何构建一个可扩展性更好的思路。
-
对于java的一些语法还不熟悉,继承接口等方面还存在一些疑问,应该更深入的去理解java这门语言
-
第一次接触面向对象语言,还是感受到了很大遍历,相信将来我会养成越来越好的面向对象思维。
-
三次作业过后在编写代码时已经很少出现代码风格的错误了,帮助我养成了很好的编程习惯。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号