POJ1797货物运输题解

首先关于这题的输出要求及背景有各OJ改动，本人也不是在POJ写的，故这里以AcWing为标准(就是因为自己菜看不懂AcWing的题解才写的......)

https://www.acwing.com/problem/content/4244(贴个链接第一次写博，如有侵权联系我立删)

读题ing:

经典的每组测试文件多组数据题(我时常怀疑这是为了用一组数据卡多组文件)，这里我待会就当成一组来分析，至于每组的衔接初始化最后贴代码会说一下

翻译为:在一个n点m条边的简单无向图上，承重是权值，求从点1到n的路径上的最小权值的最大值(莫名想到某些数学题)

//抽象为"我"要开车运货,然后我很贪,希望能多运货(赚的更多吧),但是超过每条路的承重路会塌,"我"会死,然后路费是公司报销,所以不考虑距离(那么问题来了,教练你为什么把它放最段路训练里....)

分析ing:

这题实际上考验大家的优化能力(蒟蒻见解),如何降时间。

暴力手段就是无脑dfs/bfs参数加一个min记录每条路上的最小权值,毫无疑问会爆哦

接下来的分析可能有点生硬了,因为是基于上面提到的我的教练把它放到最短路里了,所以我先尝试了bellman_ford失败了

然后想到dijkstra的贪心思想:全局最小值不可能被其他更新了

这里我反过来思考,那么要求的一条路的最大承重就也应该得从最大值开始遍历吧,这是直觉接下来具体思考

一个点它在我们的某条路径上能记下的最大权值是不是就是上一个点到它的路的权值？显然是的。那么如果我从小的权值(这里的权值是指道路上起点能走的路)开始找是不是很有可能被后面较大的权值更新啊(如果后者某条路到不了前面提到的某点则不行),所以为了尽可能少的做出多余的搜索,我们从大的边开始找

也许我表述不好,但是我们边读代码边理解吧:

/*

#include<iostream>

#include<queue>//priority_queue刚需

#include<cstring>//memset刚需

using namespace std;

const int N = 1e3 + 3,M = 1e6 + 3;//分别是点数和边数,其实理论是边数是1e9级

int T, n, m, h[N], e[M], ne[M], w[M], d[N], idx;//T即为组数,d是记录从起点到该点"路径上的最小权值的最大值"

bool v[N];//记录有没有从这个点搜过了

void add(int a,int b,int c){

    e[idx] = b;

    ne[idx] = h[a];

    w[idx] = c;

    h[a] = idx++;

}//考虑到并不是所有人都上过AcWing的网课这里说下这些数组的含义(蒟蒻看不懂大佬们的数据结构设计谁懂啊。。。),h是以某个节点为头的链头,起始指向-1(因为一开始赋了-1),在add函数的作用下逐渐拉链idx是不断后退更新的,对于一个下标的ne就是另一个下标的e,-1表示到头了，大致如下图,此处接主函数分析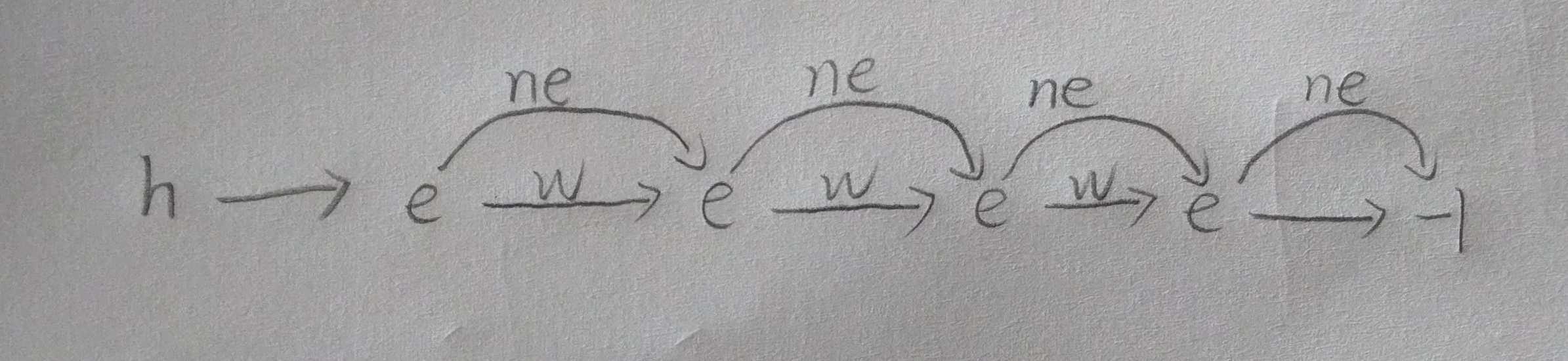

 

void dijkstra(int s){//因为是由dijkstra想到,所以还是叫这个名字吧,个人仍认为是贪心,或者理解为非模板题的应用

    memset(d, 0, sizeof d);

    memset(v, 0, sizeof v);//初始化操作

    priority_queue< pair<int,int> > q;

    d[s] = 165165165;//这里赋不会被更新即大于1e6的值就行,这里夹带私货十六谷绝美！！！

    q.push({d[s],s});//正常大根堆就行

    while(!q.empty()){

        int x = q.top().second;

        q.pop();

        if(v[x])    continue;//因为priority_queue不支持删掉非队首元素导致可能一个节点从不同点过去有多个更新操作,但是我们只需要取最大的即可,用v表示有没有取过


        v[x] = 1;

        for(int i = h[x]; i != -1; i = ne[i]){//这就是深搜

            int y = e[i];//即(u,v)中的v(这里可能要说声抱歉因为我也不知道怎么表达能让所有人看懂,图论里这样表示应该没关系吧？)

            if(d[y] < min(d[x],w[i])){//就是说如果啊,我记录到该点"路径上的最小权值的最大值"比从x到y小就更新,对于x前的路最小的就是d[x],所以只要和连接(x,y)的w比较即可

                d[y] = min(d[x],w[i]);

                q.push({d[y],y});

            }

        }

    }

}

int main(){

    scanf("%d",&T);//组数,然后因为是考虑时间复杂度,能省则省scanf和printf

    for(int i = 1; i <= T; i++){//个人喜欢while但是这题要输出序号所以for更方便些

        idx = 0;

        memset(h, -1, sizeof h);//初始化,这样每次,换一组数据用add会覆盖赋值(类比栈的操作)

        scanf("%d%d",&n,&m);

        while(m--){//while好看！！！

            int x, y, z;

            scanf("%d%d%d",&x,&y,&z);

            add(x,y,z);

            add(y,x,z);//无向图的处理


        }

        dijkstra(1);//接函数分析

        printf("Scenario #%d:\n%d\n\n",i,d[n]);//格式控制,如果不会scanf/printf还是学一下比较好(非常有用,除了字符串)

    }

   return 0;

}

/*