【TSOI】树

U606908 树

题目背景

现有一棵树，这棵树由以下代码生成。

int cnt=0;
int solve(int n){
    if(n==0){cnt++;return cnt-1;}
    int ls=solve(n-1);int rs=solve(n-1);
    adde(ls,rs);return ls;
}

其中 adde(x,y) 表示加入一条连接 \(x,y\) 的边。

可以发现，如果运行 solve(n)，可以得到一棵有 \(2^n\) 个点的树，这棵树的节点从 \(0\) 开始编号。

题目描述

现有 \(q\) 次询问，每次给出 \(x,d\)，你需要求出 \(x\) 子树上有多少个点 \(y\) 满足 \(x,y\) 在树上的最短路长度（经过的边数）等于 \(d\)。 因为这个答案可能很大，你只需要求出这个答案对 \(998244353\) 取模的结果。

然而 \(x\) 也可能非常大，因此以以下方式给出 \(x\):

对于第 \(i\) 次询问，给出 \(k_i\) 以及 \(k_i\) 个 两两不同的非负整数 \(v_1,\cdots,v_{k_i}\)，表示 \(x\) 的二进制表示中所有为 \(1\) 的位为 \(v_1,\cdots,v_{k_i}\)。

输入格式

第一行包含两个非负整数 \(n,q\)。

接下来 \(q\) 行，每行包含一次询问。

这部分的第 \(i\) 行首先包含一个非负整数 \(k_i\)，接下来 \(k_i\) 个非负整数 \(v_1,\cdots,v_{k_i}\)，最后包含一个正整数 \(d_i\)，表示询问树上与 \(x\) 的距离为 \(d_i\) 的点数。其中 \(x\) 的二进制表示中所有为 \(1\) 的位为 \(v_1,\cdots,v_{k_i}\)。

输出格式

输出 \(q\) 行，依次表示每次询问的答案对 \(998244353\) 取模的结果。

输入输出样例 #1

输入 #1

4 5
1 1 1
2 0 2 2
3 0 2 3 3
0 2
4 0 1 2 3 5

输出 #1

1
0
0
6
0

说明/提示

样例解释 #1

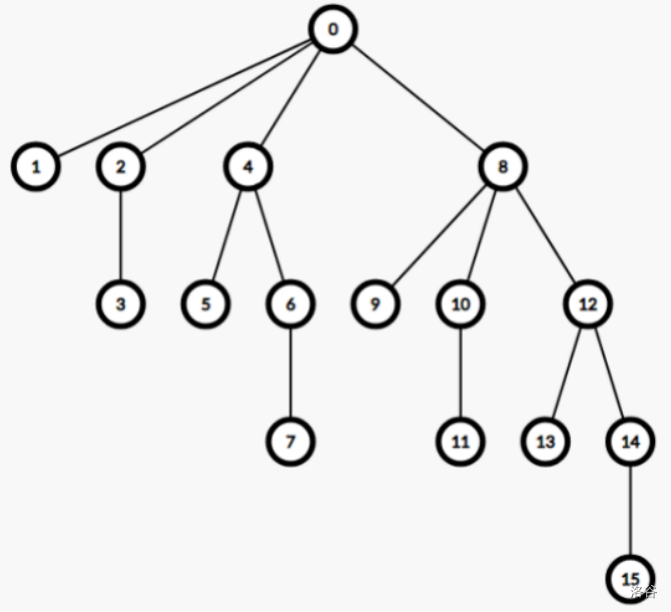
询问分别为 \((2,1),(5,2),(13,3),(0,2),(15,5)\)。

对于所有数据，保证 \(n\le 10^7,q\le 2\times 10^5,\sum k_i\le 10^6,1\le d_i\le n\)。

题解

预估绿。

std：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e7+5;
const ll mod=998244353;
int n,q;
ll ans=0;
ll fac[N],inv[N];
int ki,val[N],di;
ll ksm(ll x,ll k){
	if(k==0)  return 1;
	if(k==1)  return x%mod;
	ll t=ksm(x,k/2)%mod;
	t=t*t%mod;
	if(k&1)
	  t=t*x%mod;
	return t%mod;
}
ll c(int x,int y){
	if(x<0||y<0||x<y)  return 0;
	return (fac[x]*inv[y]%mod)*inv[x-y]%mod;
}
int main(){
	cin>>n>>q;
	fac[0]=1;
	for(int i=1;i<=n;++i)
	  fac[i]=fac[i-1]*i%mod;
	inv[n]=ksm(fac[n],mod-2)%mod;
	for(int i=n-1;i>=0;--i)
	  inv[i]=inv[i+1]*(i+1)%mod;
	while(q--){
		ans=0;
		scanf("%d",&ki);
		for(int i=1;i<=ki;++i)
		  scanf("%d",&val[i]);
		sort(val+1,val+ki+1);
		scanf("%d",&di);
		if(ki==0)  printf("%lld\n",c(n,di)%mod);
		else  printf("%lld\n",c(val[1],di)%mod);
	}
	return 0;
}