《信息学竞赛中构造题的常用解题方法》阅读笔记
from 蒋凌宇 2021 年的论文
简述
构造题在 OI 中逐渐变为一类常见题型。
不仅是 Codeforces 中几乎每一场都出现,连 NOIp 都有喵了个喵这种高级构造题的存在。
本文介绍了几种构造题的常用解法:抽屉原理、DFS 树、递归法。
抽屉原理
抽屉原理,或称为鸽巢原理,是组合数学中一个非常重要的原理。通常的表述是,若将 \(n\) 件物品放入 \(k\) 个抽屉,则其中一定有一个抽屉包含至少 \(\lceil\dfrac{n}{k}\rceil\) 件物品,也一定有一个抽屉包含至多 \(\lfloor\dfrac{n}{k}\rfloor\) 件物品。
在一些构造题中,常常会要求构造一个权值至少为(或不超过)某一个数的方案。
很多时候,可以考虑找出若干个可行的方案,使得它们的权值之和是定值。
假设找出了 \(k\) 个可行方案,其总权值和为 \(n\),由抽屉原理,这些方案中最小的权值一定不超过 \(\lfloor\frac{n}{k}\rfloor\),最大的权值至少为 \(\lceil\dfrac{n}{k}\rceil\)。
例题 1
题目
给定一张 \(n\) 行 \(n\) 列的棋盘,每个格子可能是空的或包含一个标志,标志有 \(\text{X}\) 和 \(\text{O}\) 两种。
如果有三个相同的标志排列在一行或一列上的三个连续的位置,则称这个棋盘是一个胜局,否则称其为平局。
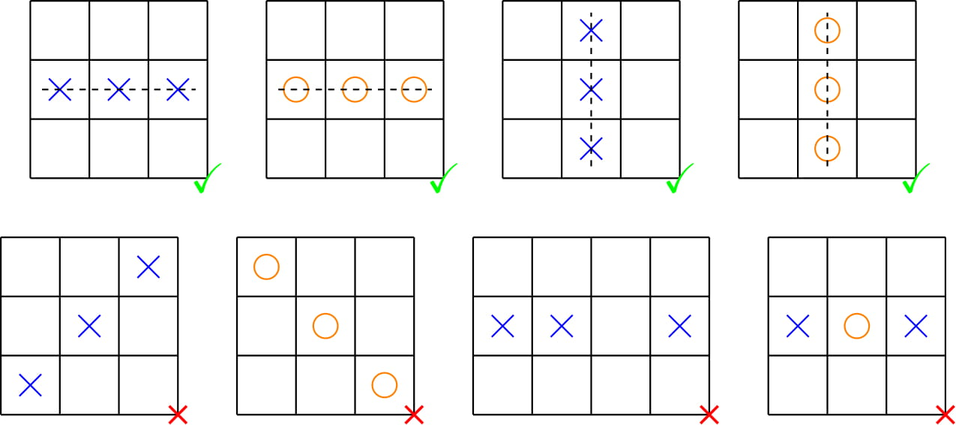
例如,上图第一行的局面都是胜局,而第二行的局面都是平局。
在一次操作中,你可以将一个 \(\text X\) 改成 \(\text O\),或将一个 \(\text O\) 改成 \(\text X\)。
设棋盘中标志的总数为 \(k\),你需要用不超过 \(\lfloor \dfrac{k}{3}\rfloor\) 次操作把给定的局面变成平局。
\(1\leq n\leq 300\)。
题目来源:CF1450C2 Errich-Tac-Toe
做法
不妨将行列都用 \(0,1,...,n-1\) 编号,将第 \(r\) 行第 \(c\) 列的格子记为 \((r,c)\)。
我们将所有格子分成 \(3\) 类,第 \(i(0\le i<3)\) 类包含所有满足 \(r+c\equiv i\bmod3\) 的格子 \((r,c)\)。
不难发现,一行或一列的连续三个格子包含第 \(0,1,2\) 类格子各一个。
于是有以下几种操作方案:
- 将第 \(0\) 类格子上的 X 都改成 O,将第 \(1\) 类格子上的 O 都改成 X。
- 将第 \(1\) 类格子上的 X 都改成 O,将第 \(2\) 类格子上的 O 都改成 X。
- 将第 \(2\) 类格子上的 X 都改成 O,将第 \(0\) 类格子上的 O 都改成 X。
显然这三种方案都能使局面变为平局。
容易发现它们的操作次数之和恰好为 \(k\),于是根据抽屉原理,它们之中操作次数最少的方案次数一定不超过 \(\lfloor\dfrac{k}{3}\rfloor\)。
于是直接构造即可。
例题 2
题目
一张扫雷地图 \(X\) 可以被视为一个 \(n \times m\) 的网格,每个格子要么是地雷格,要么不是地雷格。地雷格上没有数字,而每个非地雷格上都有一个数字,代表周围相邻 \(8\) 个格子中地雷格的数目。
给出两张尺寸均为 \(n\times m\) 的扫雷地图 \(A,B\)。每次修改可以将一个地雷格改为非地雷格,或者将一个非地雷格改为地雷格。
你可以修改最多 \(\lfloor \dfrac{nm}{2} \rfloor\) 个地图 \(B\) 中的格子,请给出一种方案,使得 \(A,B\) 中非地雷格上数字之和相同。若无解,输出 \(-1\)。
\(1\le n,m\le 1000\)。
题目来源:CF gym 102900 B Mine Sweeper II(洛谷 P9820)
做法
注意到一张地图所有空地上的数字之和等于相邻的(地雷,空地)的对数。这就意味着,如果将一张地图的所有地雷改成空地,所有空地改成地雷(我们记这个操作为翻转),其所有空地上的数字和不变。
于是就有以下两种方案:
- 将 \(A\) 改成 \(B\)。
- 将 \(A\) 改成 \(B\) 上述翻转后的结果。
因为每个格子只会恰好在一种方案中被修改,因此这两种方案的操作次数之和恰好为 \(nm\)。取较少的一种,其操作次数一定不超过 \(\lfloor \dfrac{nm}{2} \rfloor\)。
DFS 树
在解决一些图上的构造问题时,DFS 树往往有非常大的帮助。
一张图的 DFS 树是在对其进行深度优先遍历时,所形成的树结构。
建立了 DFS 树后,图上的边可以分成四类:
- 树边是每个点到其孩子结点的边,也是每个点第一次被访问时经过的边。
- 前向边是每个点到其后代的边,不包括树边。
- 后向边是每个点到其祖先的边。
- 其余边称为横叉边。
其中后三种边统称为非树边。
在构造题中,通常我们用到的是无向图的 DFS 树。如果我们将每条边按照第一次经过时的方向进行定向,则无向图的 DFS 树满足所有非树边都是后向边。这个性质在解题过程中有非常大的作用。
例题 1
题目
给出一张 \(n\) 个点的无向连通图和一个常数 \(k\)。
你需要解决以下两个问题的任何一个:
- 找出一个大小为 \(\lceil\frac k2\rceil\) 的独立集。
- 找出一个大小不超过 \(k\) 的环。
独立集是一个点的集合,满足其中任意两点之间在原图上没有边直接相连。
\(3\le k\le n\le10^5\),\(n-1\le m\le2\times10^5\),\(1\le u,v\le n\)。
题目来源:CF1364D Ehab's Last Corollary
做法
记 \(l=\lceil\frac k2\rceil\)。
先建出图的 DFS 树。对于每条非树边 \((u,v)\)(如上文所说,它是后向边),如果 \(|\text{dep}_u-\text{dep}_v|<k\) 则取该边以及树上对应的路径即为一个长不超过 \(k\) 的简单环。
否则,考虑两种情况:
- 若 \(m=n-1\),即图是树,把点按照深度奇偶性分为两个集合,其较大集合一定是大小至少为 \(\lfloor\frac n2\rfloor\ge l\) 的独立集,取其中 \(l\) 个点即可。
- 若 \(m>n-1\),即非树边不满足 \(|\text{dep}_u-\text{dep}_v|<k\)。这说明 DFS 树深度至少为 \(k\),且任意一对深度差在 \([2,k)\) 间的点不存在边相连。设深度最大的点为 \(x\),取 \(x\) 和其 \(2,4,...,2l-2\) 级祖先,即为所求。
时间复杂度 \(O(n+m)\)。
例题 2
题目
给定一张 \(n\) 个点 \(m\) 条边的无向连通图,以及三个整数 \(a,b,c\),满足 \(a+b+c=n\)。你需要将 \(n\) 个顶点分成三个集合 \(A,B,C\),大小分别为 \(a,b,c\),使得其中至少两个集合是连通的(集合中的任意两个点能只经过该集合内的点互相到达)。有可能无解。
\(3\le n\le 10^5,2\le m\le 2\cdot 10^5\)。
题目来源:P5811 IOI2019 景点划分
做法
不妨设 \(a<b<c\),则只需要保证 \(A\) 和 \(B\) 是连通的即可。因为此时如果 \(A\) 和 \(C\) 连通可以通过将 \(C\) 的一些定点加入 \(B\) 中使 \(C\) 的大小变为 \(b\),依然合法。\(B\) 和 \(C\) 连通同理。
这时我们可能会卡住,因为我们并没有发现有解的条件,难以下手。因此我们来先考虑图是一棵树的情况。
图是一棵树时,\(A\) 和 \(B\) 都是其中的子树。因此一定存在一条边使得 \(A\) 和 \(B\) 处于边的两侧。
我们只需要找到一条边使其两侧较小和较大的子树大小分别不小于 \(a\) 和 \(b\) 即可。
一条边两侧较大的子树一定包含重心,所以我们可以考虑对重心进行分析。
如果删去重心后最大的连通块大小小于 \(a\) 则无解,否则设其大小为 \(x\)。
由重心的性质显然有 \(x\le\frac n2\),因此删除这棵子树后还剩 \(n-x\ge \frac n2\) 个点。又因为 \(b\le\frac n2\)(因为 \(b\le c\)),所以这棵子树和重心之间的边就是我们要找的。
回到一般情况,我们建立图的 DFS 树。
找到 DFS 树的重心 \(u\),记 \(u\) 上方的子树为 \(T\),下方子树为 \(S_1,S_2,...,S_k\)。考虑几种情况:
- 如果 \(T\) 或某个 \(S_i\) 大小不小于 \(a\),则我们可以用和树一样的方法构造。
- 否则,就需要考虑无向图 DFS 树的性质。不同 \(S_i\) 之间没有边相连,同时有一些 \(S_i\) 与 \(T\) 相连。如果所有与 \(T\) 相连的 \(S_i\) 加上 \(T\) 的大小之和仍然小于 \(a\),则必然无解,因为这代表 \(A\) 和 \(B\) 都要包含重心 \(u\)。否则,从 \(T\) 开始依次加入与 \(T\) 相连的 \(S_i\) 直到大小不小于 \(a\)。设为 \(X\),则可以在其中选出 \(A\)。由于 \(T\) 和所有 \(S_i\) 大小都小于 \(a\),\(X\) 的大小不超过 \(2a\),删除 \(X\) 后剩余点数至少为 \(n-2a\ge b\),可以选出 \(B\)。
时间复杂度 \(O(n+m)\)。
递归
在一些构造题中,对于不同的输入,问题的结构有很大的相似性。在很多时候,这往往意味着我们的构造也具有很大的相似性或具有周期性。这时,我们往往可以通过递归的方式,对子问题进行构造,并在子问题的构造的基础上进行一些小的调整,来得到原问题的构造。
需要指出的是,递归可以作为一种思想,但在实际解题过程中可能有代码、时空复杂度高的缺点,需要选手灵活运用。
例题 1
题目
有 \(2n\) 个包裹,其中有 \(n\) 个 A 类包裹和 \(n\) 个 B 类包裹,初始时排列如下:
这些包裹占据了编号为 \(1\) 至 \(2n\) 的格子,同时还有编号为 \(-2n+1\) 到 \(0\) 的 \(2n\) 个空格子可以使用。现在要将它们重新排列,使得它们形如
即这些包裹占据相邻的 \(2n\) 个格子(不一定是 \(1\) 到 \(2n\))且所有 A 类包裹在所有 B 类包裹左边。
排列过程由若干次操作构成,每次操作可以选择相邻的两个包裹(不能只选择一个)并将它们移动至某两个相邻空格中。
给定 \(n\),找到一个最短的操作序列。
\(3\le n\le 100\)。
题目来源:CF gym 101221 A Baggage
做法
与通常的构造题不同,本题要求的为最短操作序列,看起来难以下手。但是经过尝试或对较小的 \(n\) 进行搜索,会发现它们的最短操作序列长度都是 \(n\)。
证明操作次数不少于 \(n\) 并不麻烦:考虑有多少对相邻的包裹类型相同,设为 \(d\)。初始时 \(d=0\),目标状态的 \(d=2n-2\)。一次操作中,取出包裹时 \(d\) 不会增加,而放回时假设放的位置为 \(t\) 和 \(t+1\),则只可能增加 \((t-1,t)\) 和 \((t+1,t+2)\) 这两对。容易发现第一次操作至多使 \(d\) 增加 \(1\),因此总操作次数不少于 \(1+\lceil\frac{2n-3}2\rceil=n\)。
接下来就要尝试对于所有 \(n\) 构造长为 \(n\) 的操作序列。对于 \(n\) 较小时可以直接搜索出操作序列。
观察发现,在 \(n>3\) 的情形中,我们都是将这些包裹从编号为 \(1\sim 2n\) 的格子移到编号为 \(-1\sim 2n-2\) 的格子。
于是我们定义 \(solve(n,x)\) 表示将包裹从编号为 \(x+1\) 到 \(x+2n\) 的格子(形如初始状态)移到编号为 \(x-1\) 到 \(x+2n-2\) 的格子并排列成形如目标状态。
通过对较大的 \(n\) 的情形的观察,对于 \(n\ge 8\) 的情况有如下构造(其中 \(\texttt/\) 表示空格子):
在这里,我们发现最后一行的红色部分正好符合 \(solve\) 函数的输入,因此我们调用 \(solve(n-4,x+4)\)。
至此,我们便完成了长度为 \(n\) 的操作序列的构造。
例题 2
题目
一个 \(n\) 个点 \(m\) 条边的无向图,你需要选择一个点集 \(S\),满足:
- 一条边 \((u,v)\) 是开启的当且仅当 \(u\in S\) 或 \(v\in S\),则任意一对点都可以只经过开启的边互相到达。
- 不存在一条边 \((u,v)\) 满足 \(u\in S\) 且 \(v\in S\)。
有可能无解。
\(2\le n\le 3\cdot 10^5,0\le m\le 3\cdot 10^5\)。
题目来源:CF1470D
做法
显然如果原图不连通则无解。
猜测原图连通时一定有解,考虑归纳证明。当 \(n=1\) 时,显然 \(\varnothing\) 合法。假设 \(n=k-1\) 时一定有解,考虑 \(n=k\) 的情况。
删除一个非割点的点(这样的点一定存在),设为 \(v\),则 \(G\) 去掉 \(v\) 后是一个 \(k-1\) 点的连通图。由归纳假设,其有一组解 \(S'\)。接下来考虑两种情况:
- 若 \(G\) 中至少一个与 \(v\) 相邻的点属于 \(S'\),则令 \(S=S'\) 即可。
- 否则,\(G\) 中与 \(v\) 相邻的点都不属于 \(S'\),则令 \(S=S'\cup \{v\}\) 即可。
于是我们证明了有解当且仅当图连通。但是每次寻找一个非割点复杂度太高,无法接受。
观察归纳过程,其实只需要按照任意 DFS 序依次加入点即可。
时间复杂度 \(O(n+m)\)。
本题其实比例题 1 更容易,但放在这里主要代表递归思想不一定要出现在代码中。
总结
构造题的考察越来越频繁,但对许多选手来说,解决一道构造题并不容易。这里介绍了解题过程中的几个较常用的解题思路,希望能够让大家有所启发。
这些仅仅是构造题中的冰山一角,希望读者在训练过程中,也能对构造题的解法进行归纳、总结,并分享给大家。同时也希望更多有趣的构造题能出现在算法竞赛中。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号