AI之旅(6):神经网络之前向传播
前置知识
求导
知识地图
回想线性回归和逻辑回归,一个算法的核心其实只包含两部分:代价和梯度。对于神经网络而言,是通过前向传播求代价,反向传播求梯度。本文介绍其中第一部分。
多元分类:符号转换
神经网络是AI世界的一座名山,这座山既神秘又宏大。看过的人都说好,但是具体好在哪里,却不易用语言表述。只有一步一步耐心爬上去,登顶之后才能俯瞰风景。
毫无疑问登顶的过程不会一帆风顺,总会遇到大大小小的困难,然而一旦我们对困难有了心理准备,登顶也不再是件难事。只是看文章不易理解,一起拿出笔和纸吧。
在逻辑回归中,特征经过参数的线性组合,作用于激活函数得到预测结果。我们可以将特征视为输入层,将预测结果视为输出层。逻辑回归模型和函数如下所示:
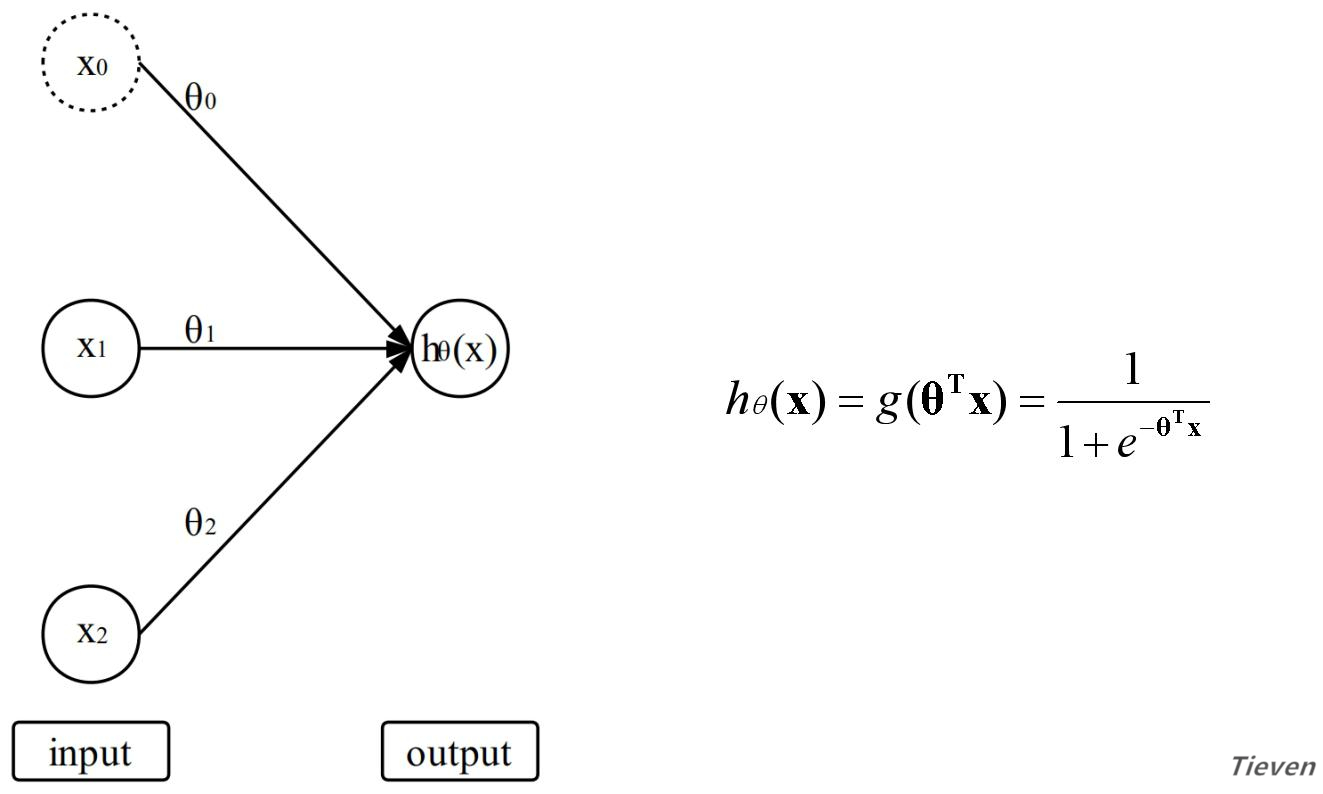
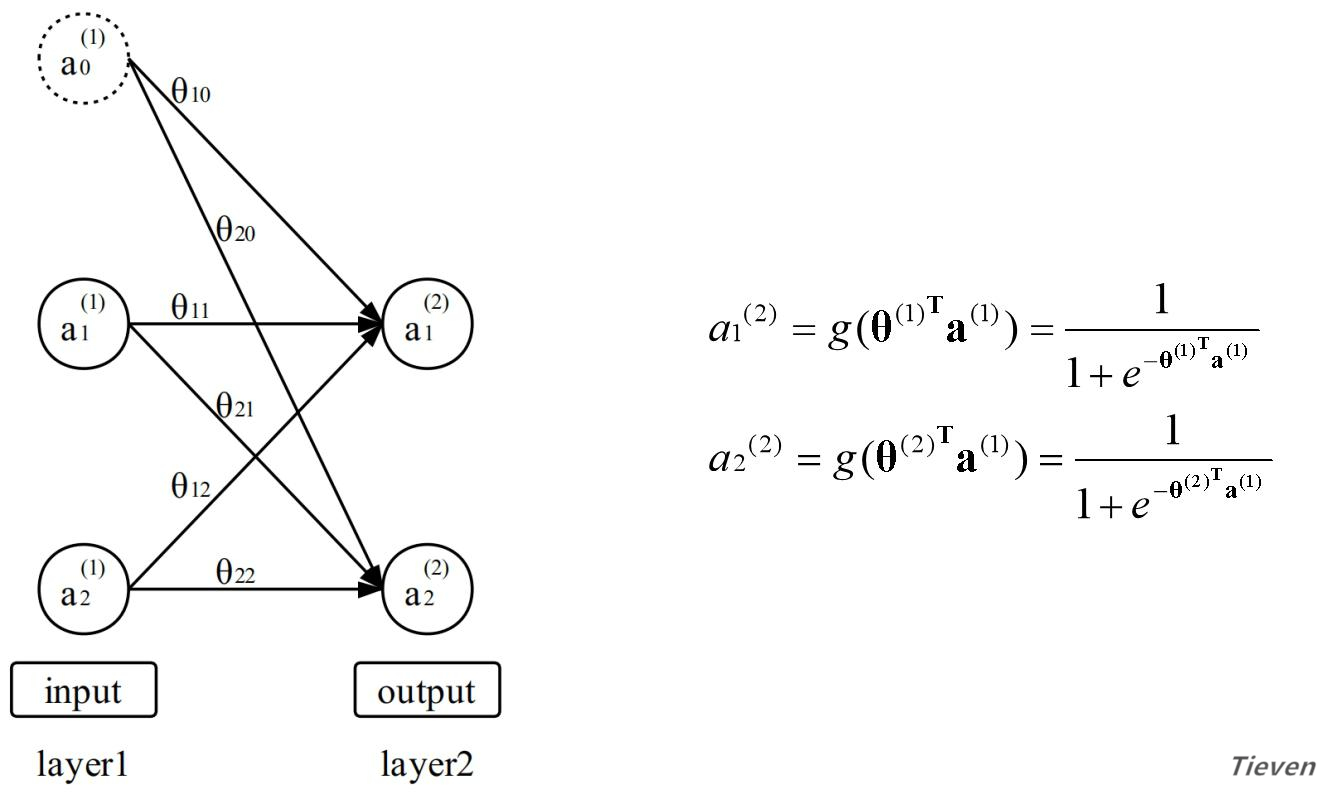
上图如果从层的角度看,也可以将输入层视为第一层,将输出层视为第二层。为了方便接下来的叙述,需要用一套新的符号来表示特征和预测结果,上图可转化为以下形式:
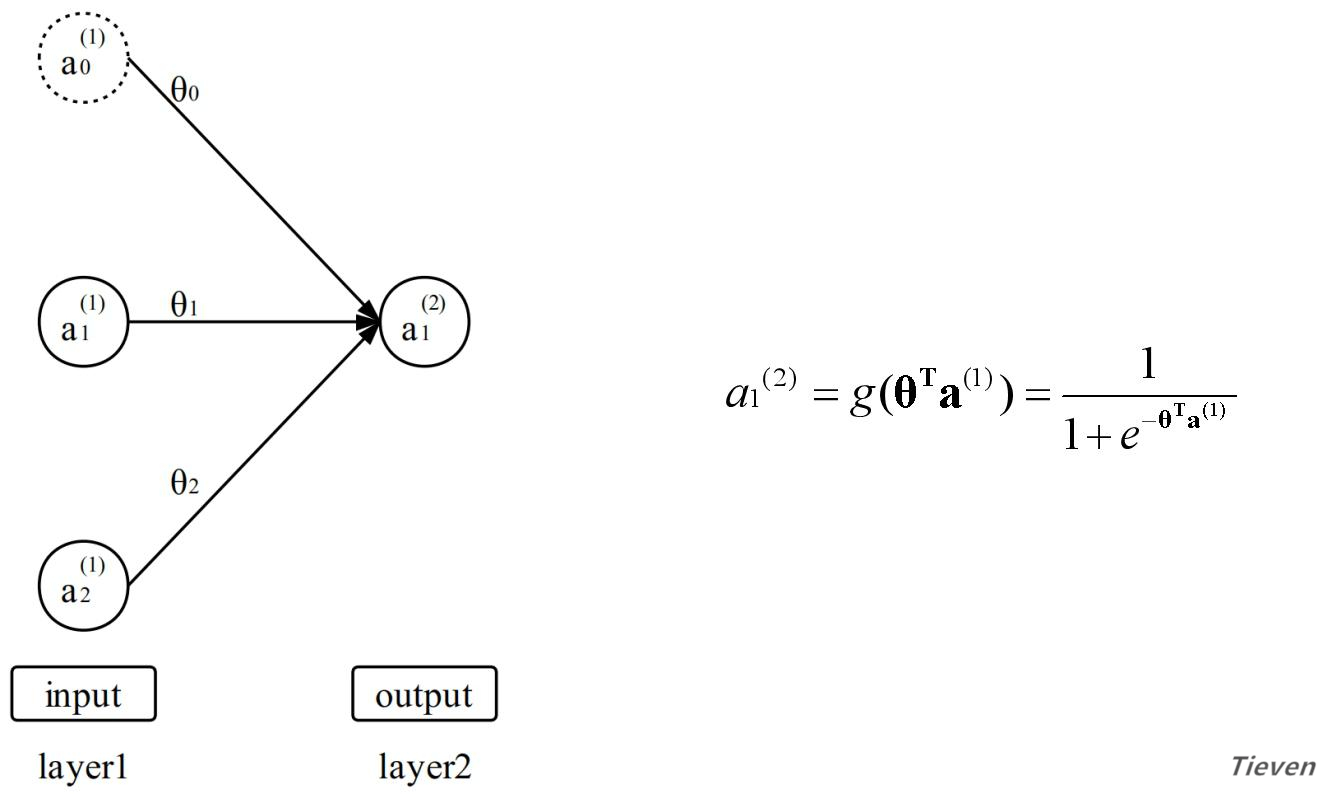
a表示激活项,每一层的激活项等于前一层的激活项经过线性组合,作用于激活函数的值。特别约定用特征作为第一层的激活项。因此以下两句话是同一种含义的不同表述:
1,预测结果等于特征经过线性组合,作用于激活函数的值;
2,第二层的激活项等于第一层的激活项经过线性组合,作用于激活函数的值;
多元分类:矩阵形式的参数
一个逻辑回归模型可以实现二元分类,如果将多个逻辑回归模型组合起来,便可以实现多元分类。用同一个样本的特征训练两个逻辑回归分类器可以表示为以下形式:
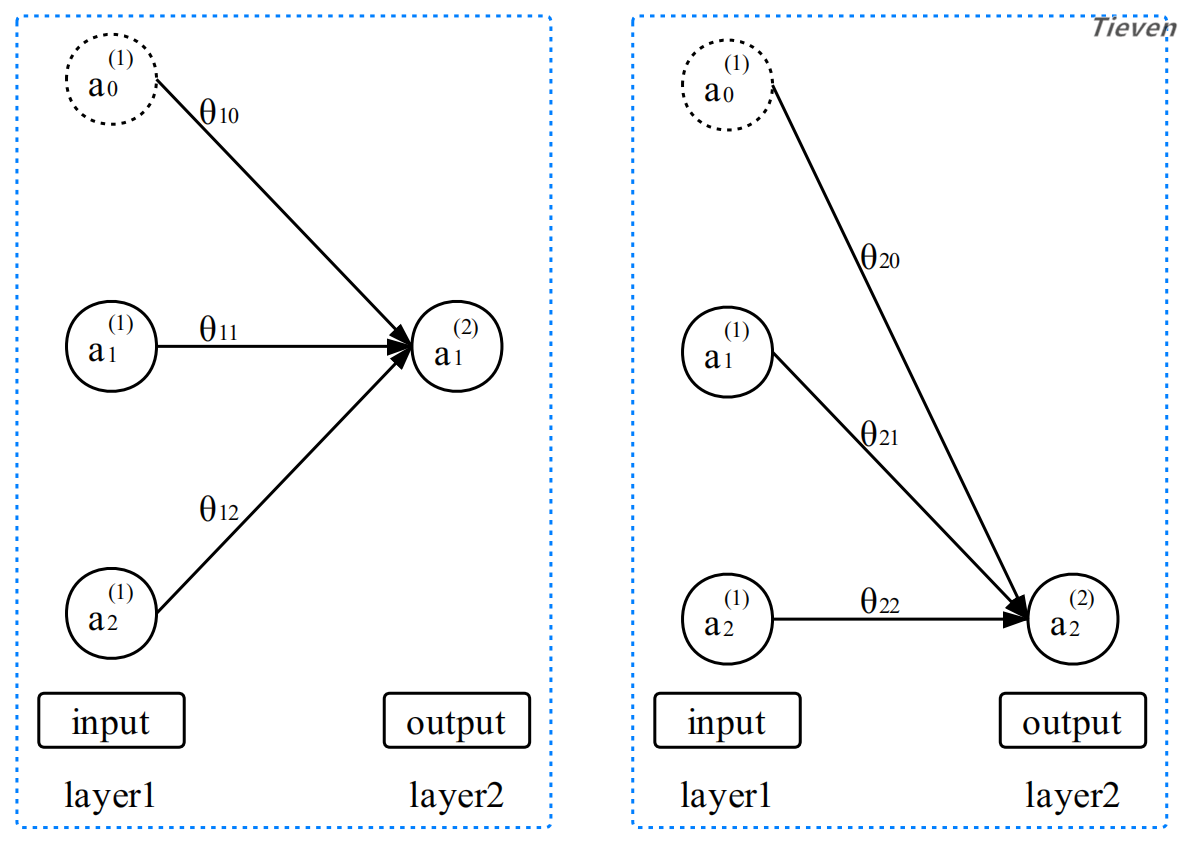
因为特征是相同的,所以可以组合为以下形式:
注:实际构建的多元分类模型中包含着2个以上的分类器,比如3个,4个,10个。无论包含几个分类器,模型的本质是相同的,这里为了表述简便以2个分类器为例。
在二元分类模型中,参数是以向量的形式表示。在多元分类模型中,参数是以矩阵的形式表示。虽然表示形式改变了,但是其工作的机制没有变化,如下图所示。
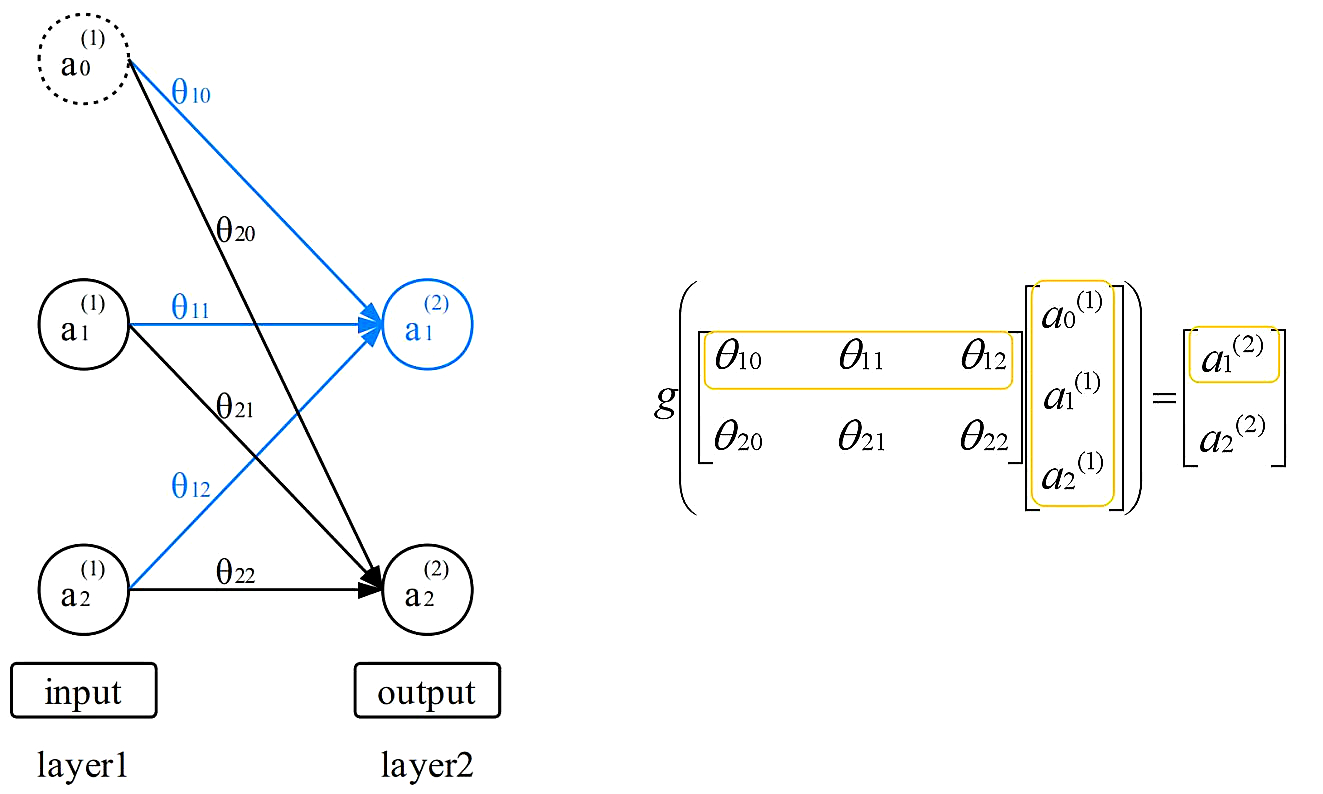
“第二层的第一个激活项等于第一层的激活项经过线性组合,作用于激活函数的值”。以上两幅图是从不同角度对同一种情况的描述,将参数写成矩阵的形式可以表述地更加简练。
多元分类:向量形式的标签
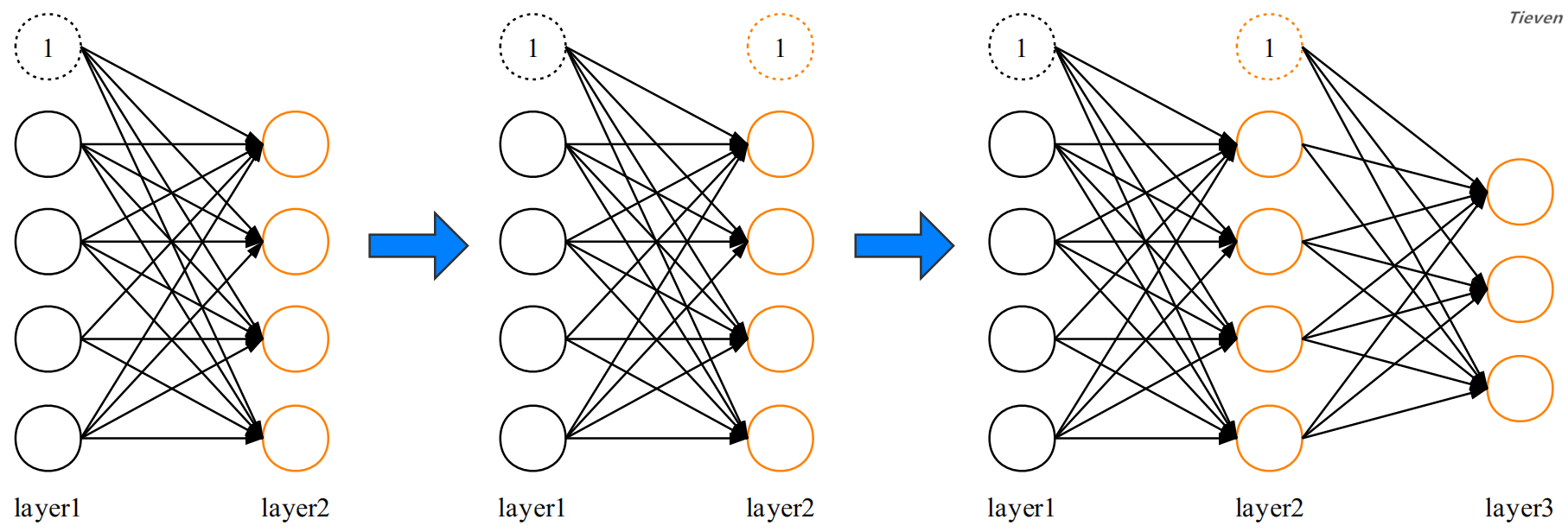
在二元分类中,可以通过0和1来表示两个类别。在多元分类中,模型无法直接识别1,2,3这样的数字,需要将数字转换成二进制向量的形式,以3个类别的花为例。

当传入一个样本的特征时,3个分类器对该组特征分别进行判断,所预测的结果也是用二进制向量的形式表示,如下图所示:
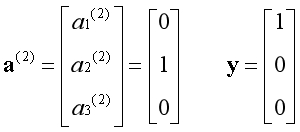
第一个分类器说:不是第一种花;
第二个分类器说:是第二种花;
第三个分类器说:不是第三种花;
样本是第一种花,而模型预测是第二种花,显然这是一次失败的预测。以上是假设的极端情况,实际上每个分类器都会给出样本属于该类别的概率,以最大的概率为准。
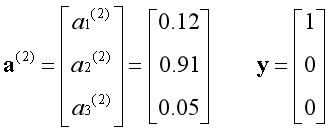
假设有6个样本,需要将标签转化为矩阵的形式传入算法。若每次只用一个样本训练时,算法会将对应样本的标签抽取出来使用。注意矩阵的下标,Z表示分类器的数量。
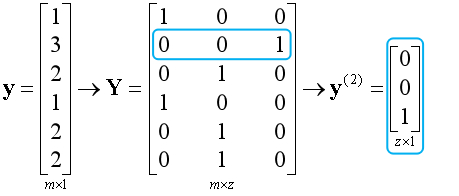
模型结构:隐藏层
神经网络是在多元分类模型的基础上,增加了隐藏层的结构。隐藏层也是由激活项组成,隐藏层中激活项的数量没有限制,隐藏层的总层数也没有限制。如下图所示:
上图是一个包含2个隐藏层的神经网络。对比前面的多元分类模型,我们发现神经网络似乎可以视为若干个多元分类模型的组合。这两者到底有什么联系呢?
相同点:两者都是由激活项组成,每一层的激活项等于前一层的激活项经过线性组合,作用于激活函数的值。特别约定用特征作为第一层的激活项。
不同点:多元分类用输入层(特征)训练得到输出层(预测结果)。神经网络用输入层(特征)训练得到隐藏层,用隐藏层训练得到输出层(预测结果)。
不同点:多元分类通过特征直接得到预测结果,预测结果为第二层激活项的值。神经网络通过特征间接得到预测结果,预测结果为最后一层激活项的值。
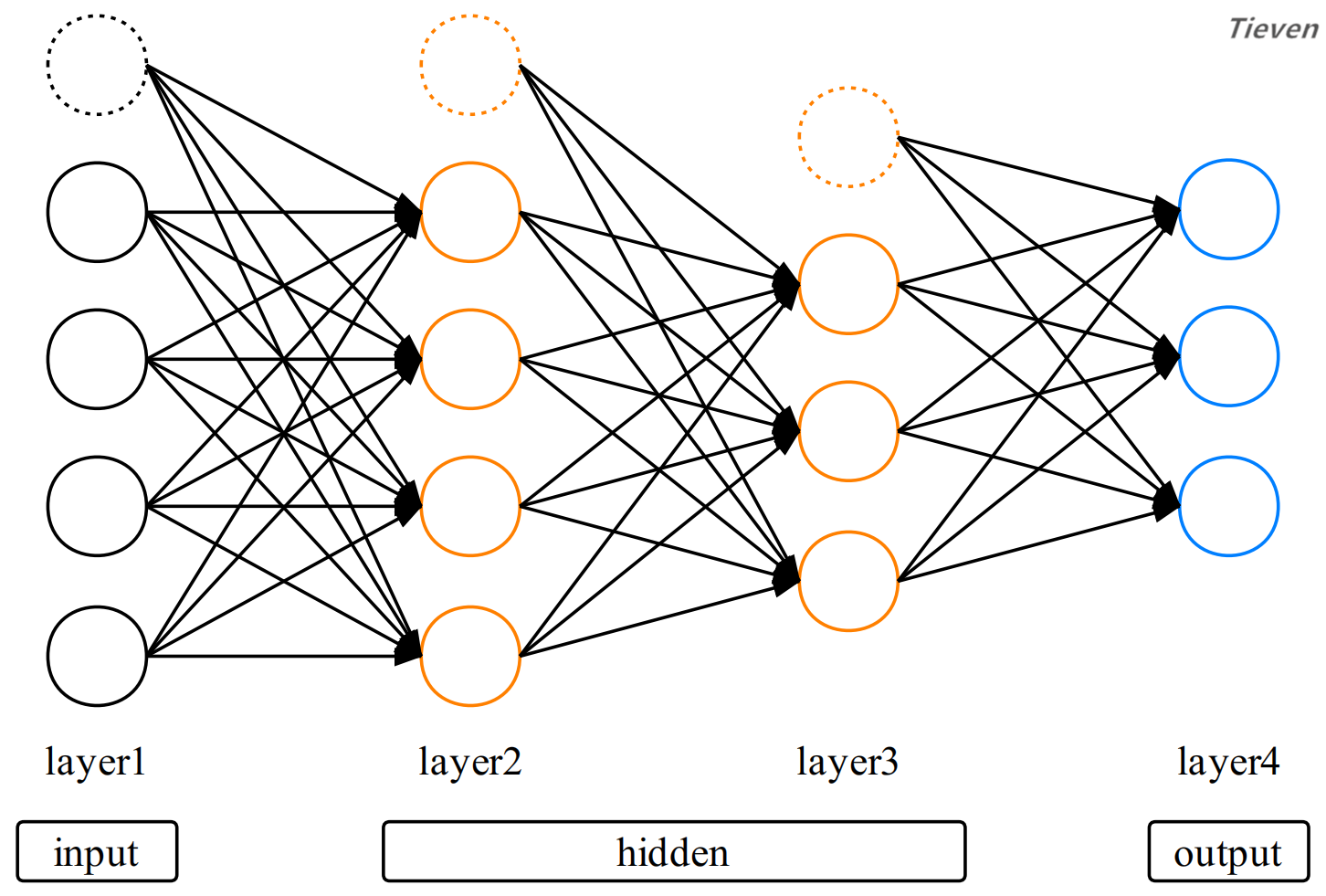
模型结构:偏置单元
记得在逻辑回归中,我们会在样本的特征中添加元素1作为常数项,常数项可以调节模型使之发挥更好的性能。在神经网络中将常数项称为偏置单元,偏置单元的值为1。
对于神经网络的每一层而言,都是将前一层视为特征进行训练。如果只关注第二层和第三层,可以发现这是一个多元分类模型。此时将第二层视为特征,因此需要加上偏置单元。
每层的偏置单元与前一层没有联系,只用于后一层的训练。例如第二层的偏置单元与第一层没有联系,只用于第三层的训练。注意最后一层为输出层,输出层不需要偏置单元。
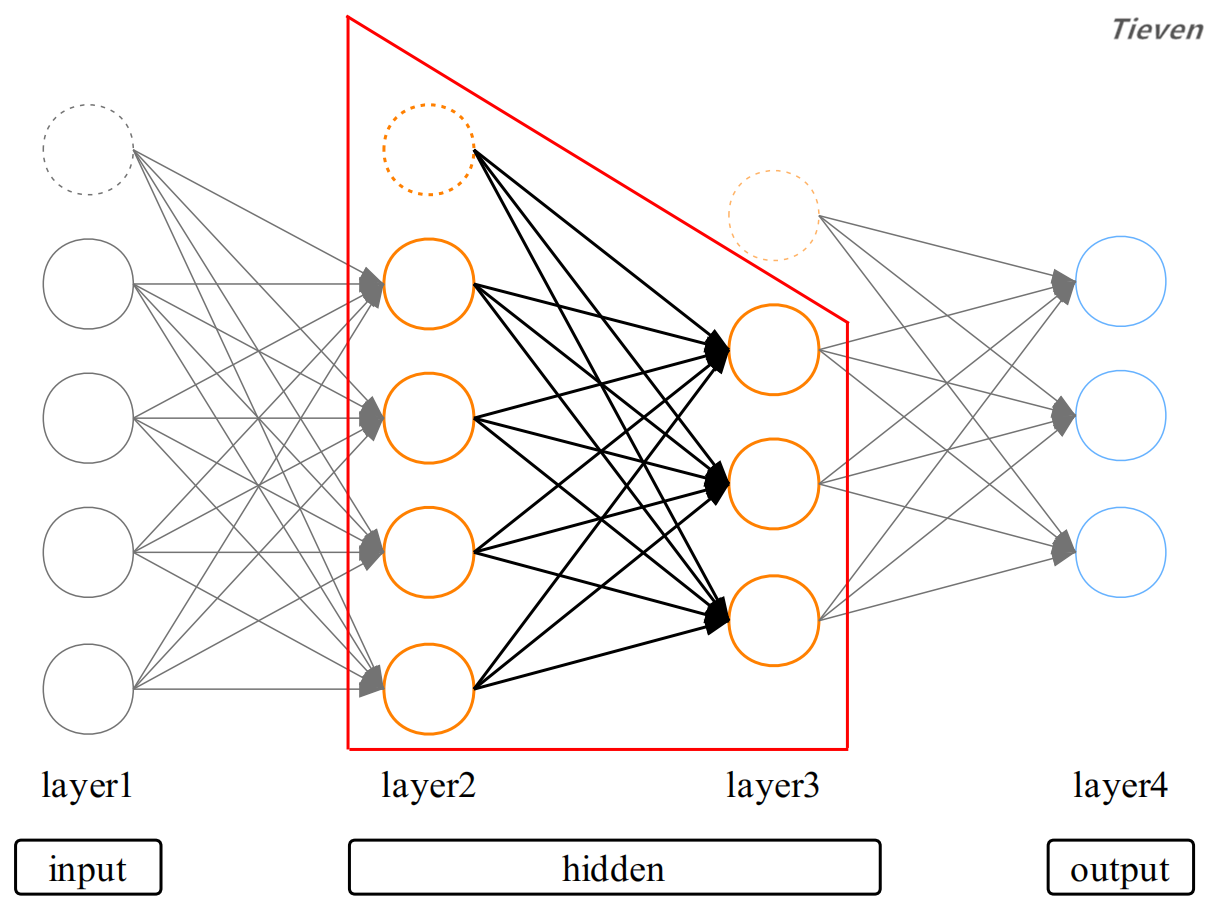
至此我们对神经网络的结构有了大致的了解,它可以视为多个多元分类模型的组合。接下来需要对激活项做更深入的认识,为此重新构建一个更简单的例子,并添加上符号。
激活项

添加上符号之后,图像似乎一下子变复杂了。仔细观察会发现数字之间存在明显的规律。一共只有两种符号,激活项和参数。偏置单元属于特殊的激活项,用虚线表示。

左图表示第k层的第i个激活项(i从0开始计数);
右图表示第k个参数矩阵中第j行,第i列的参数(i从0开始计数);
在实际应用中,是通过矩阵和向量的形式表示神经网络的结构,为后续的向量化计算做准备,首先系统定义一下将要用到的符号。
m:样本数;
k:神经网络层数;
K:神经网络总层数(此例中K=4);
S_k:第k层的单元数量(不包含偏置单元)(此例中S_2 = 2);
Z:分类器的数量(此例中Z=2);
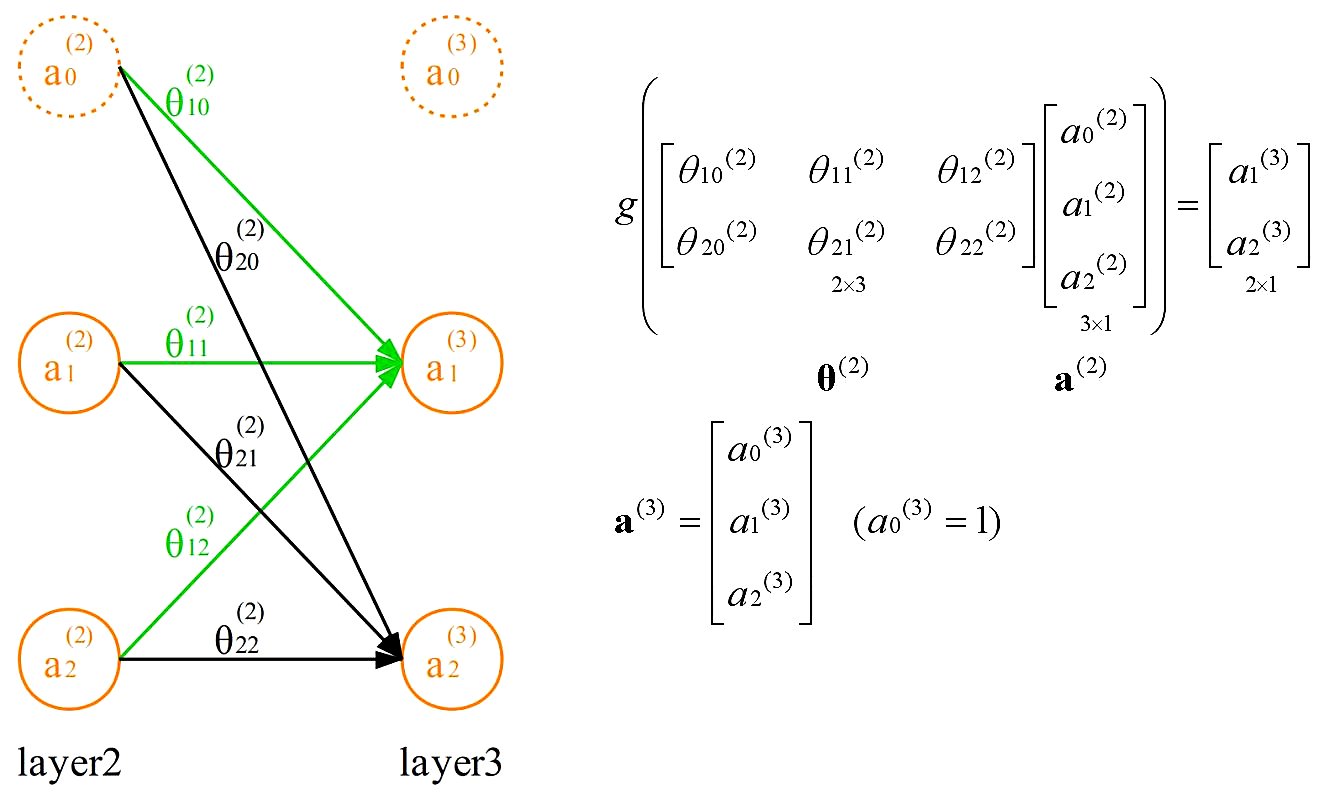
通过第一个参数矩阵,从第一层激活项获得第二层激活项,为第二层激活项添加偏置单元:

通过第二个参数矩阵,从第二层激活项获得第三层激活项,为第三层激活项添加偏置单元:
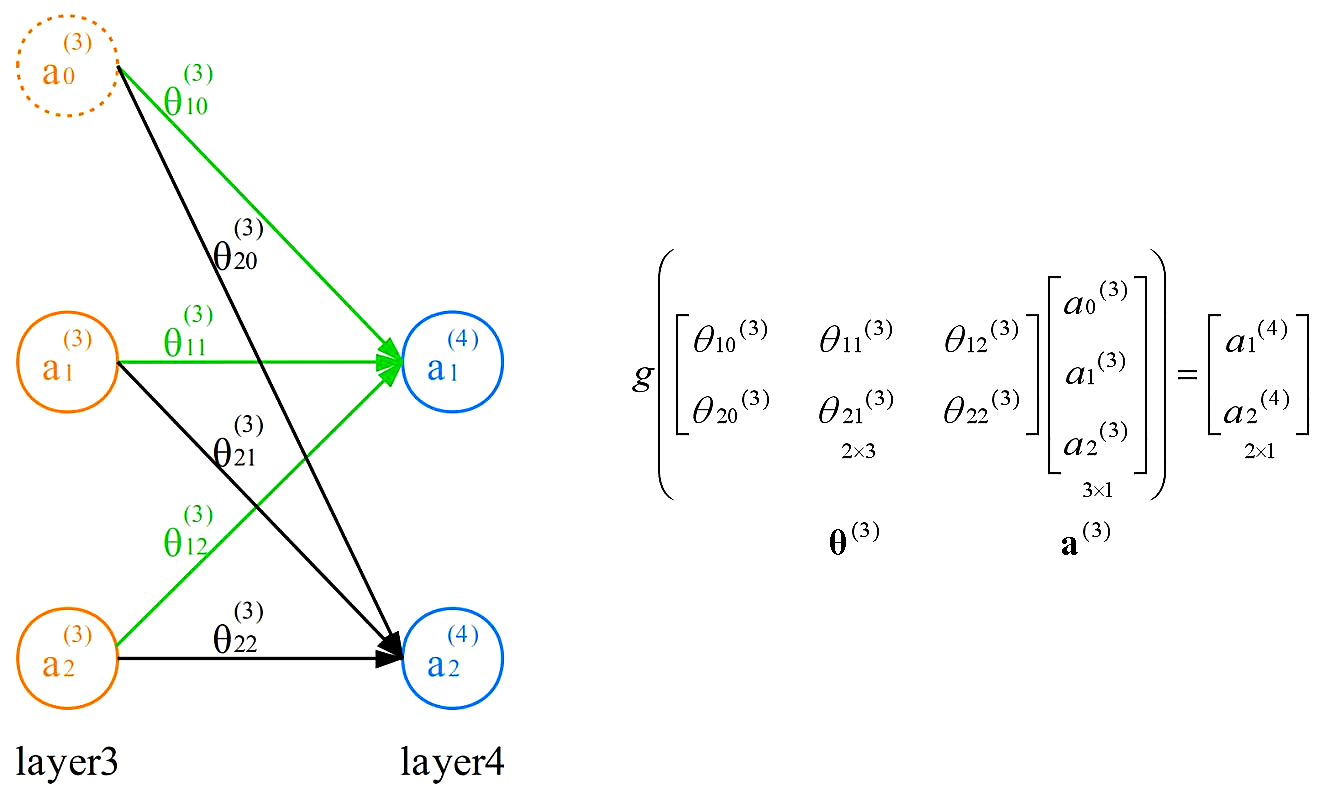
通过第三个参数矩阵,从第三层激活项获得第四层激活项,第四层激活项为预测结果,预测结果不添加偏置单元:
注:在神经网络中参数的初始值不能为0,否则模型将无法工作,一般将其随机初始化为一个较小的数字。
前向传播
观察这3个参数矩阵,有没有发现矩阵的尺寸存在对应关系?以第1个矩阵为例,矩阵的行数等于下一层的单元数,矩阵的列数等于本层的单元数加1。用公式表示:
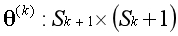
感觉复杂是正常的,偏置单元的存在会造成理解上的困难,计数上的麻烦,以及实现中的障碍。好消息是这已经是神经网络中主要的两个难点之一,我们已经走完一半的路程。
目前已经知道每一层的激活项产生的机制,也知道最后一层激活项即预测结果,我们可以写出神经网络的代价函数,已知逻辑回归的代价函数是如下形式:
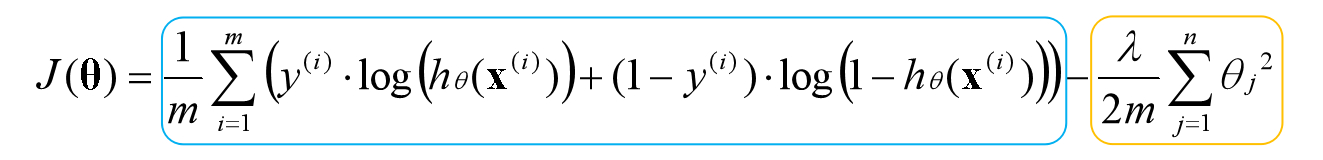
为了便于理解,将神经网络的代价函数分两部分来写,最后再组合起来。上式是只有一个分类器的代价函数,在例子中我们有两个分类器,第一部分可以写为如下形式:
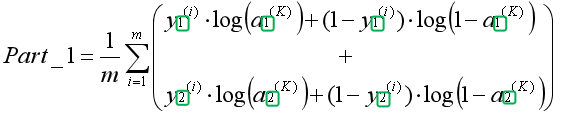
因为最后一层激活项即预测结果,所以用最后一层激活项表示假设函数。绿色方框中的下标表示属于第几个分类器。我们用Z表示分类器的数量,因此可写为如下形式:
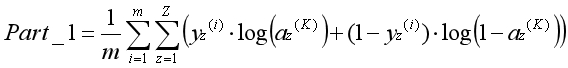
正则化是通过为参数支付代价的方式,降低系统复杂度的方法。在逻辑回归中常数项对应的参数不参与正则化,同理,在神经网络中偏置单元对应的参数不参与正则化:
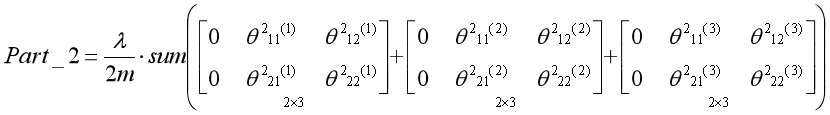
每个参数矩阵的第一列即偏置单元对应的参数,通过几步简单的矩阵操作,即可将上述形式的矩阵元素累加。如果再简练一点可以用方程的形式表示,稍微有点抽象:
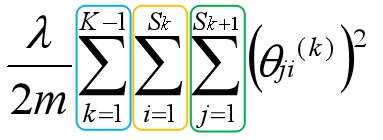
蓝色:从第1个矩阵到第K-1个矩阵(4层网络,对应3个参数矩阵);
橙色:矩阵的第1列到最后一列(i从0开始计数);
绿色:矩阵的第1行到最后一行(j从1开始计数);
至此得到了完整的神经网络代价函数,目标是最大化该代价函数。通过求导我们可以得到局部最优解,但无法得到全局最优解,不同初始化参数的值会影响局部最优解的选择。
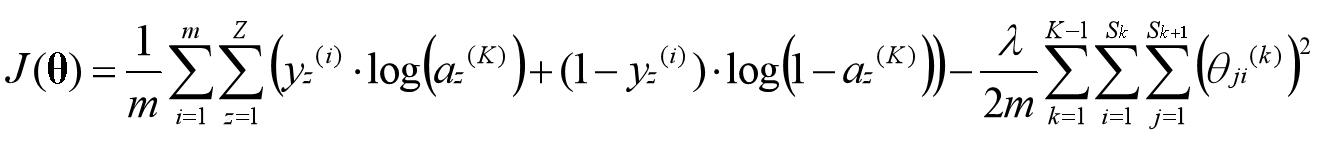
总结
目前为止我们掌握了什么?我们已经可以构建一个具有任意数量的隐藏层,支持向量化操作,包含正则项的深度神经网络。只差最后一步就可以让这个强大的网络运作起来。
我们从二元分类开始,用多个分类器构造了多元分类模型,使用激活项作为模型的基本单位。将参数转换为矩阵的形式,将标签转换为向量的形式,为得到神经网络做好了准备。
通过添加隐藏层的方式从多元分类扩展到神经网络,发现神经网络可视为多个多元分类模型的组合。而偏置单元是神经网络中特殊的激活项,这也是算法的难点之一。
通过将模型转换为矩阵和向量的形式,最终得到了神经网络的代价函数。至此已经实现了神经网络的前向传播。在下一篇中,我们将通过对代价函数求导,实现神经网络的反向传播。
版权声明
1,本文为原创文章,未经作者授权禁止引用、复制、转载、摘编。
2,对于有上述行为者,作者将保留追究其法律责任的权利。
Tieven
2019.1.11
tieven.it@gmail.com


 浙公网安备 33010602011771号
浙公网安备 33010602011771号