求局部最小值

题目：给定一个数组，每两个相邻的数组不等，找到该数组上任意一个局部最小值。

定义：nums[1] > nums[0] , 下标0位置就是局部最小值
nums[len(nums) - 2] > nums[len(nums) - 1] ,下标n-1位置就是局部最小值
nums[n-1] > nums[n] && nums[n] < nums[n+1] ,下标n位置就是局部最小值

题目解析

通过上面的定义已知三种情况

1. 第一个数小于第二个数
2. 最后一个数小于倒数第二个数
3. 左右两边的数都比中间这个数大
   第一种和第二种很好判断，关键在于第三种情况。如果出现第三种情况说明不符合第一种和第二种情况。也就是说nums[1] < nums[0] 和nums[n-1] < nums[n] && nums[n] > nums[n+1].
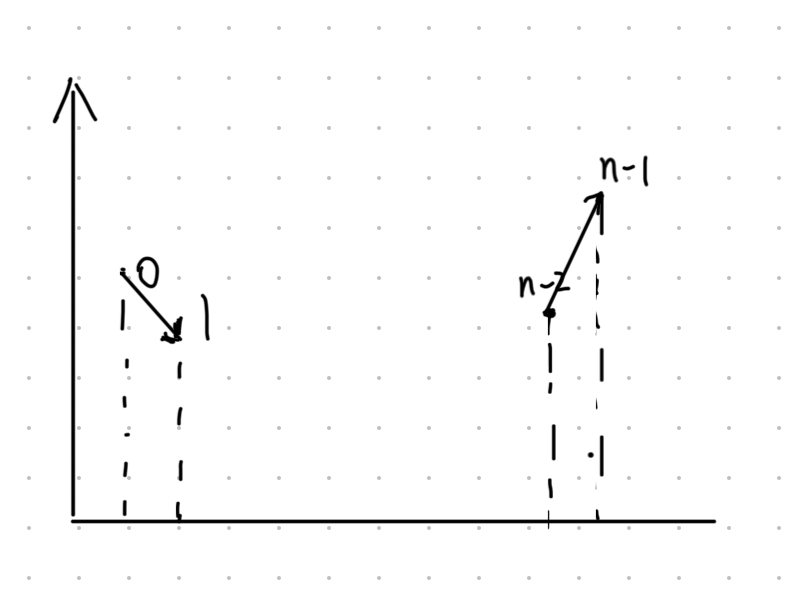
   第一个数比第二个数大，说明他是向下的趋势。最后一个比倒数第二个大，说明是向上的趋势。那么先向下再向上必然存在局部最小值。
   画图解析：
   
   必然存在局部最小值。

# 求局部最小值
def part_most_min(nums):
    if nums is None or len(nums) == 0:
        return -1
    if len(nums) == 1:
        return 0
    # 检查左边界
    if nums[0] < nums[1]:
        return 0
    # 检查右边界
    if nums[-1] < nums[-2]:
        return len(nums) - 1
    left, right = 1, len(nums) - 2
    while left <= right:
        mid = left + (right - left) // 2
        # 如果中间元素比两边都小，就是局部最小值
        if nums[mid] < nums[mid - 1] and nums[mid] < nums[mid + 1]:
            return mid
        # 如果中间元素比左边大，局部最小值在左边
        elif nums[mid] > nums[mid - 1]:
            right = mid - 1
        # 如果中间元素比右边大，局部最小值在右边
        else:
            left = mid + 1

    return left